1、docker-compose介绍

Docker Compose是一个用于快速配置多个Docker容器的工具。它是一个定义和运行多容器的Docker应用工具，通过YAML文件配置自己的服务，然后通过一个命令，就能使用配置文件创建和运行所有的服务。Docker Compose能够简化在开发环境中设置多个容器应用程序的过程，并在多个容器之间进行通信和协调。

Docker Compose将所管理的容器分为三层，分别是工程（project），服务（service）以及容器（container）。Docker Compose运行目录下的所有文件（docker-compose.yml，extends文件或环境变量文件等）组成一个工程，若无特殊指定工程名即为当前目录名。

Docker Compose的工程配置文件默认为docker-compose.yml，可通过环境变量COMPOSE_FILE或-f参数自定义配置文件，其定义了多个有依赖关系的服务及每个服务运行的容器。Compose允许用户通过一个单独的docker-compose.yml模板文件（YAML格式）来定义一组相关联的应用容器为一个项目（project）。

2、docker-compose build

需要build的场景：dockerfile变化了 或者 build目录下的内容(文件)变化了

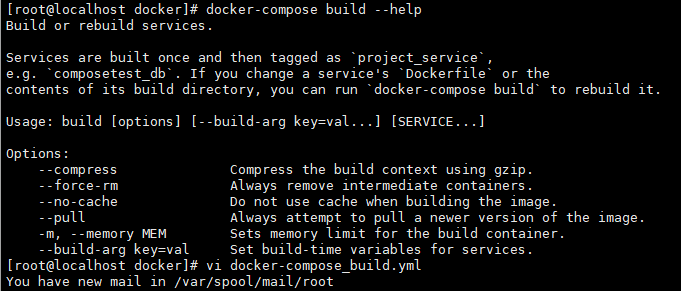
3、docker-compose down

down命令的作用：默认情况下，down命令仅仅删除容器和compose file内配置的网络。如果网络和卷被标记为external 则从不删除网络和卷。

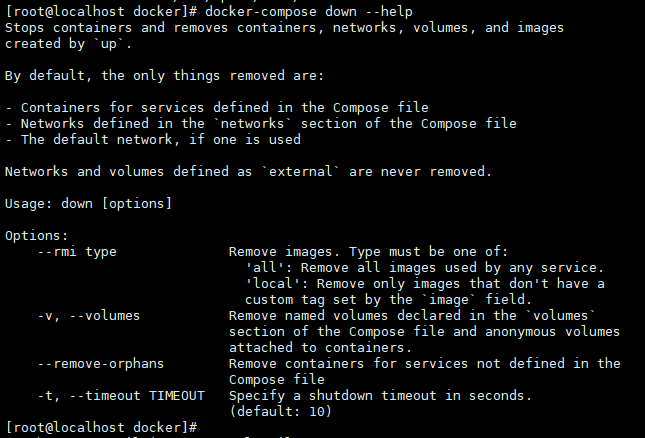
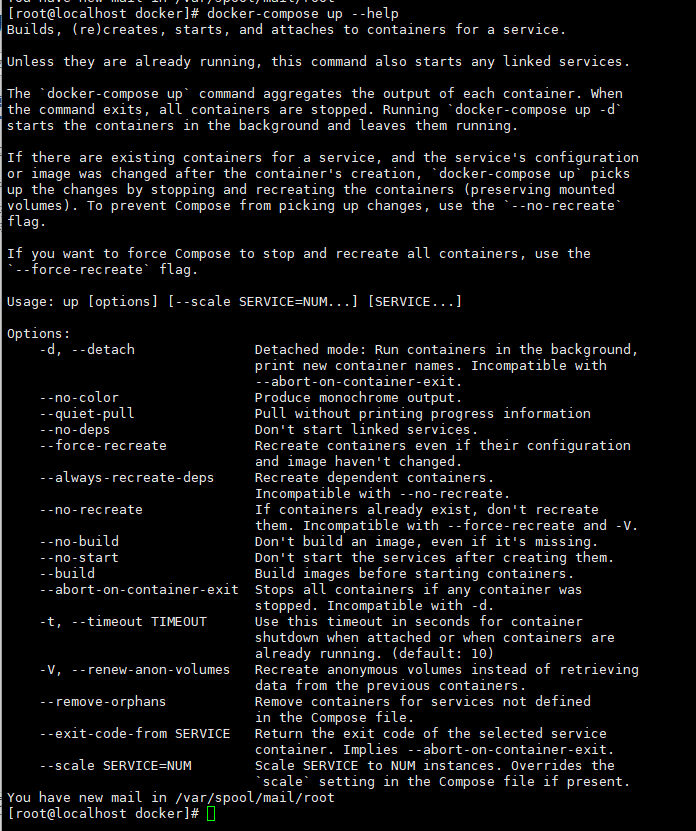
4、docker-compose up -d

up命令的作用：创建容器
特别地，如果在一个容器创建后，这个容器的配置文件被改变了，docker-compose up -d 会停止、启动容器以应用到这个改变。