目录
定时类型
8253内部结构框图
8253命令字
六种工作方式及输出波形
计数初值的计算与装入
8253的初始化
定时类型
可编程定时器8253：（内部采用的是16位 减法计数器）
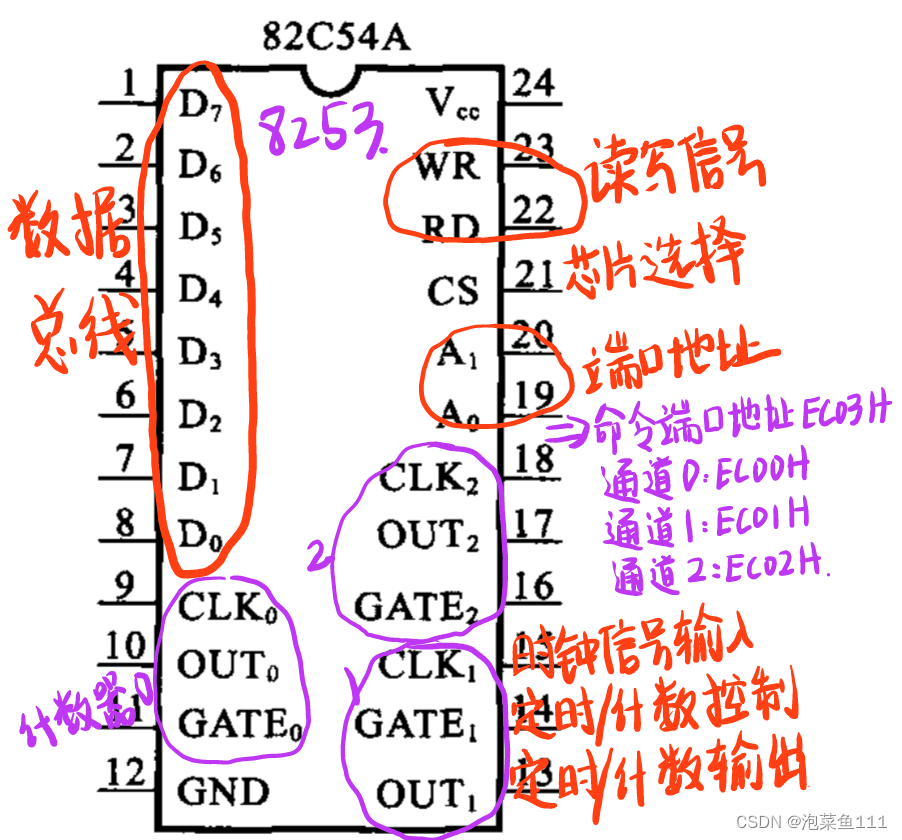
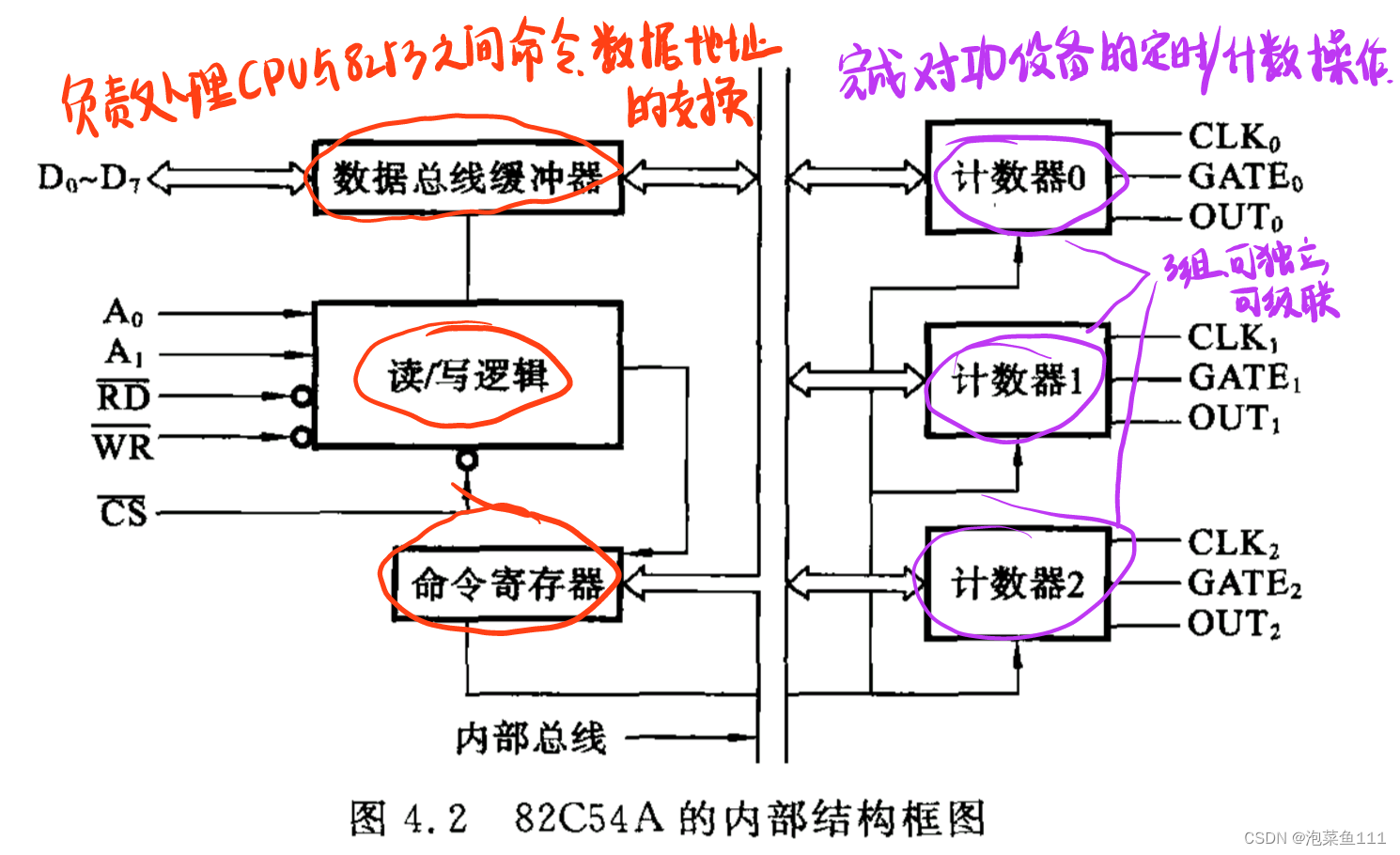
8253内部结构框图
8253命令字
8253有三个命令字：方式命令，锁存命令，读回命令。（三个命令共用一个端口，按方式命令在前，其他命令在后的顺序写入。）
方式命令格式： （方式命令用来初始化8253，所以必须使用，剩下两个根据需要使用）
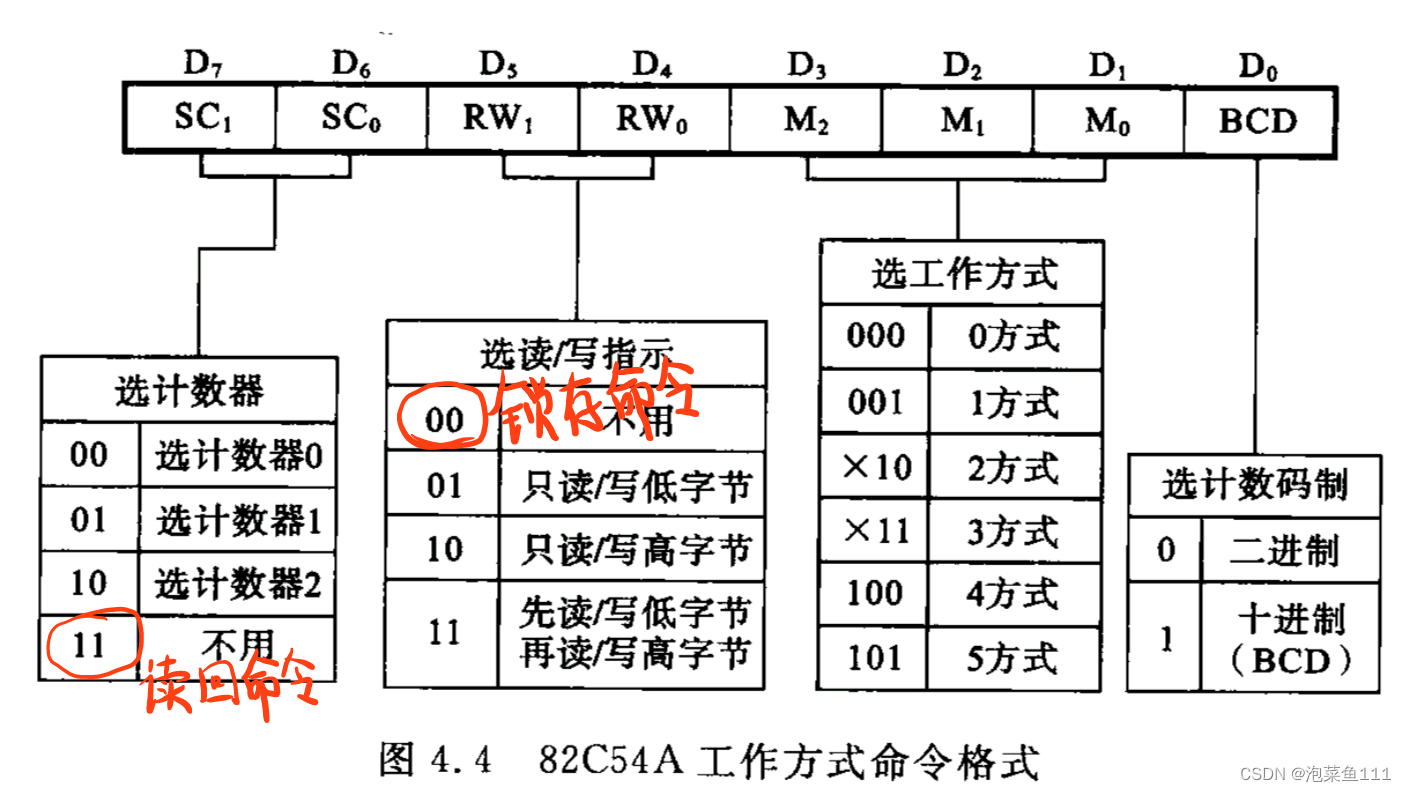
例：计数器1，只读/写低字节，方式1，二进制
01010010 52H
MOV A, 52H
MOV DPTR, #EC03H
MOVX @DPTR, A锁存命令格式： （在要求读取当前计数值时使用）
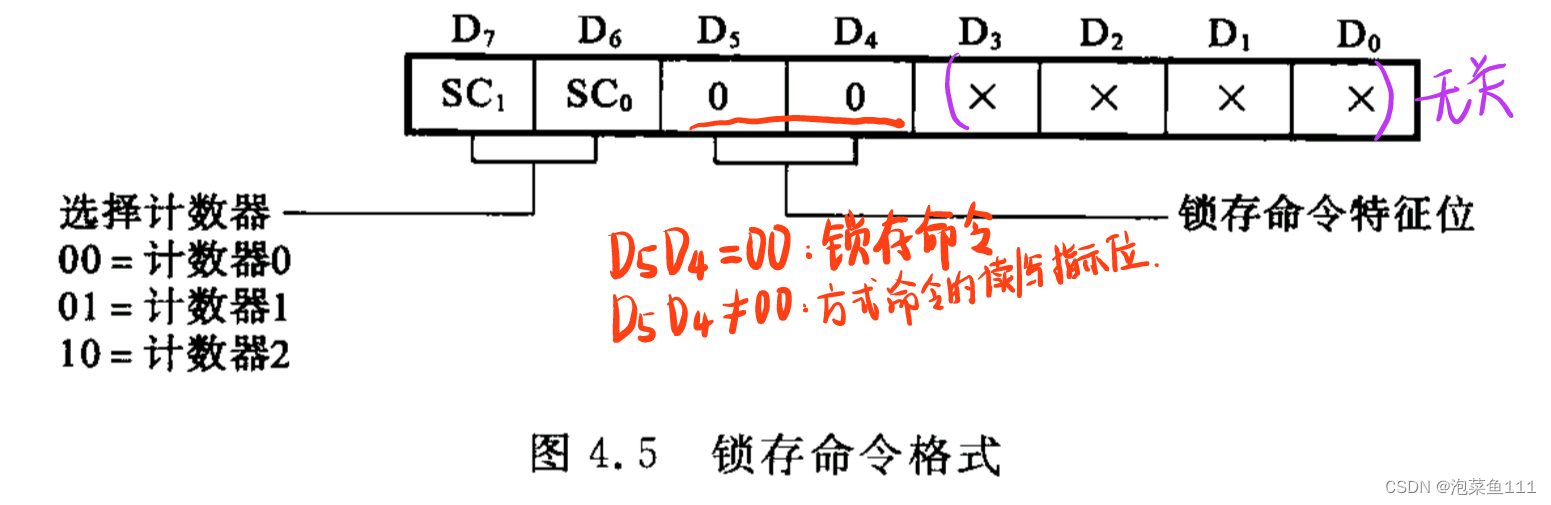
例：读计数器1的当前值，送到30H 31H中：01 00 0010 42H 方式1 二进制 MOV A, #42H
MOV DPTR, #EC03H 命令端口地址
MOVX @DPTR, AMOV DPTR, #EC01H 通道1
MOVX A, @DPTR
MOV 30H, AMOV DPTR, #EC01H 通道1
MOVX A, @DPTR
MOV 31H, A读回命令格式：（既能锁存计数值又能锁存状态信息，一条读回命令可以锁存3个计数器的当前计数值和状态）
读取计数器2的当前计数值：11011000
读取计数器2的当前状态： 11101000
读取计数器2的当前计数值和状态：11001000
读取全部3个计数器的当前计数值和状态：11001110读取计数器1的当前计数值，送到30H 31H中：1110 0010 E2H MOV A, #0E2H
MOV DPTR, #EC03H 命令端口地址
MOVX @DPTR, AMOV DPTR, #0EC01H 数据低八位
MOVX A, @DPTR
MOV 30H, AMOV DPTR, #0EC01H 数据高八位
MOVX A, @DPTR
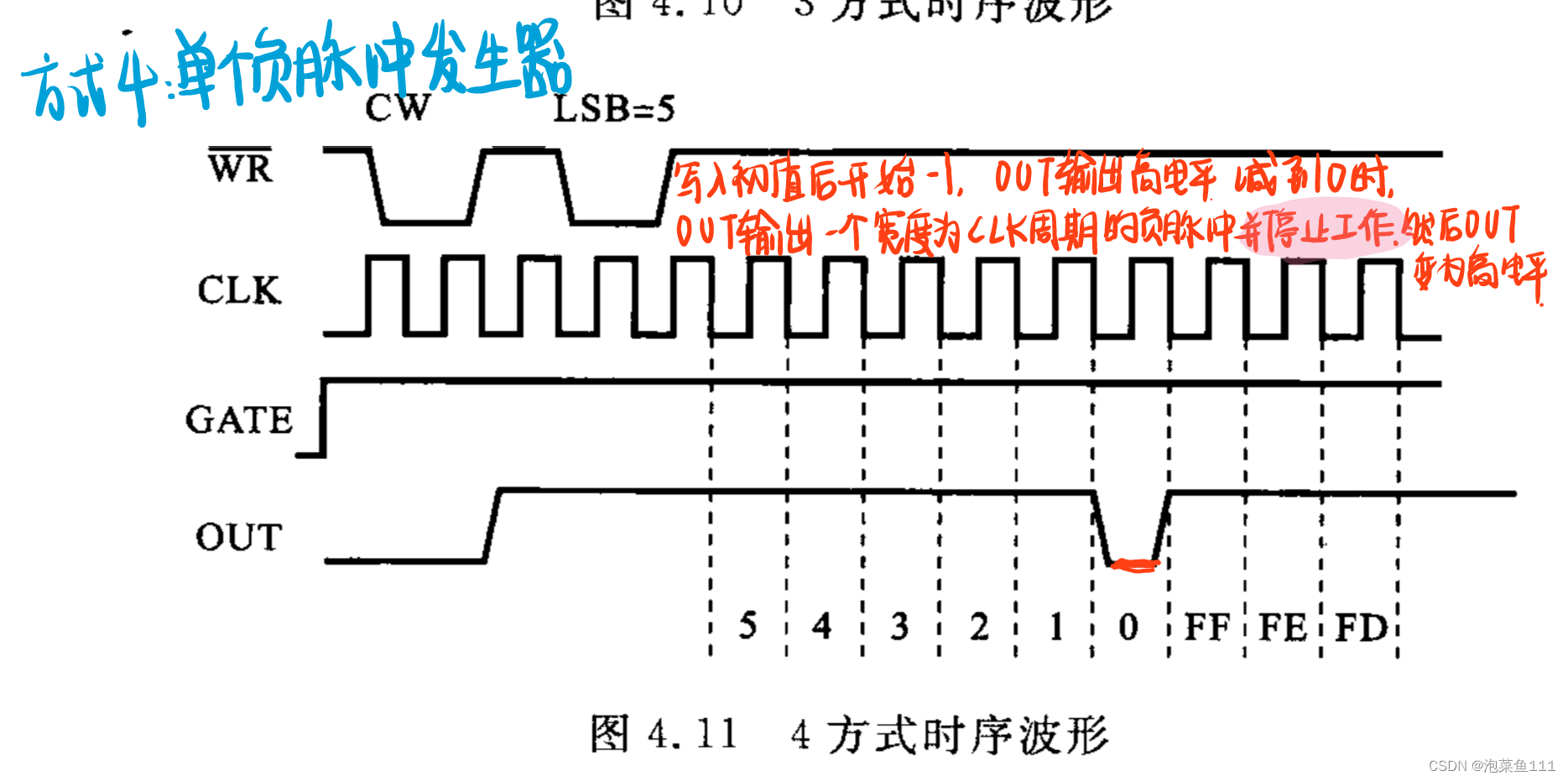
MOV 31H, A六种工作方式及输出波形
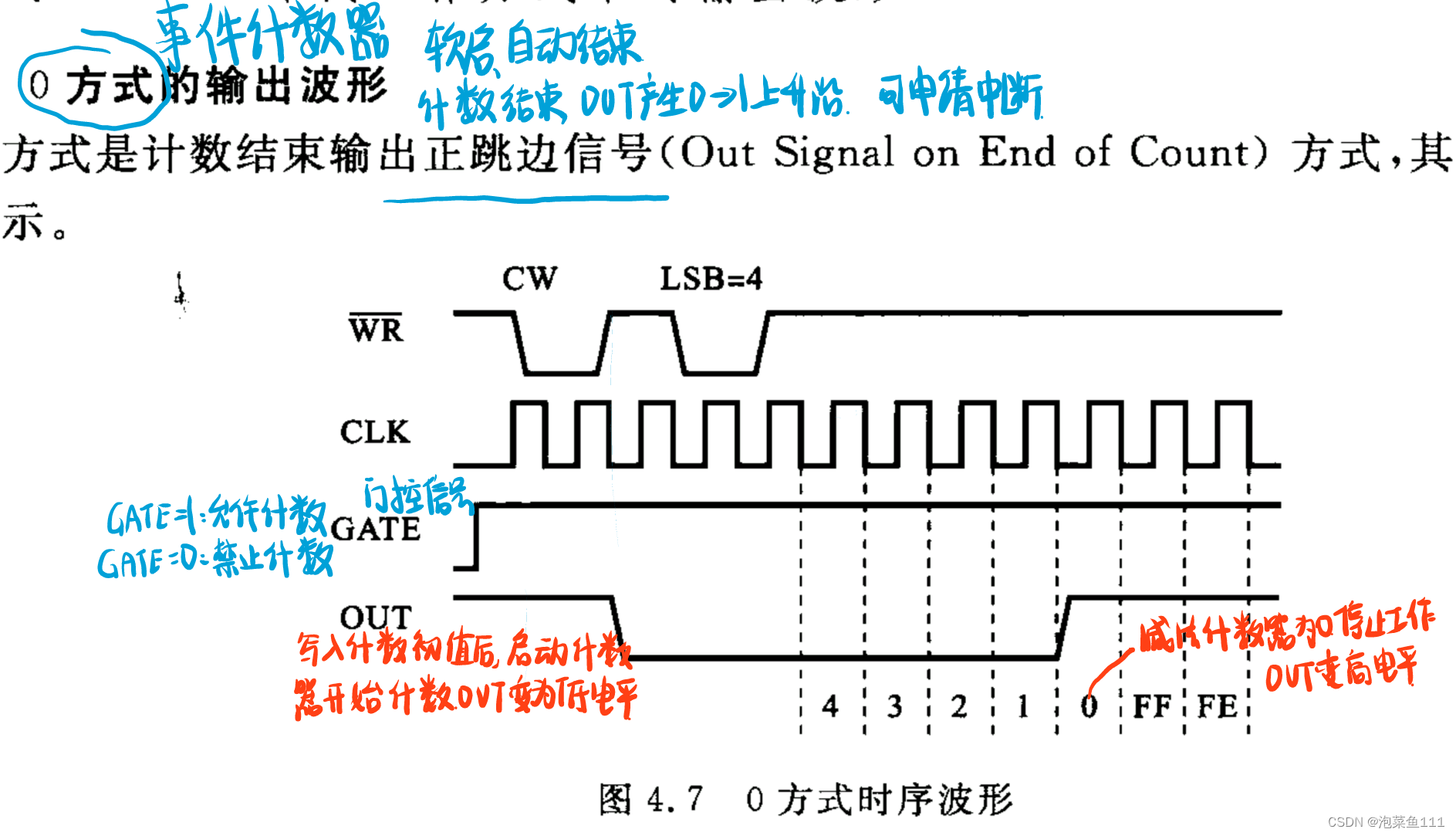
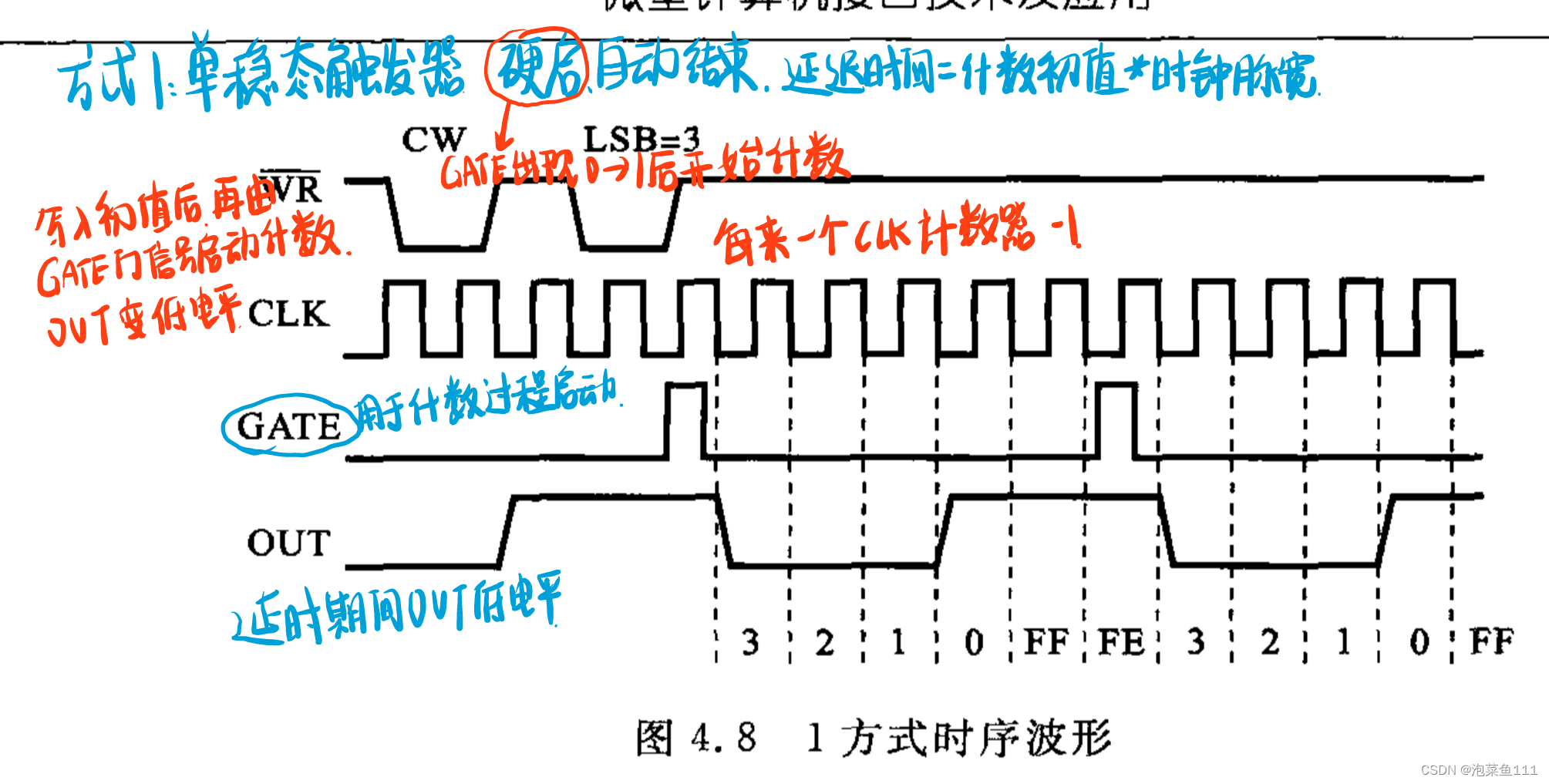
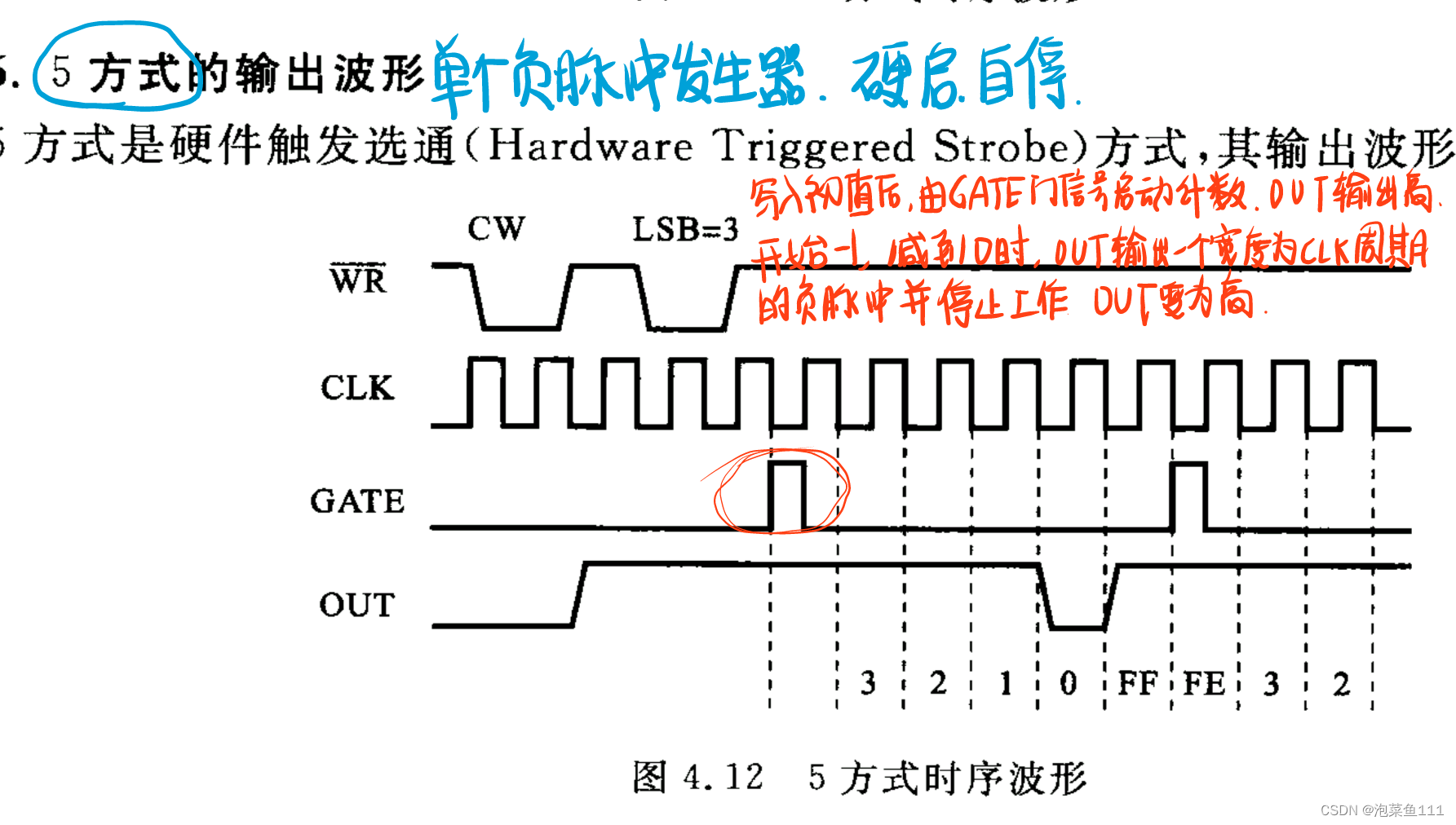
启动方式：软件启动（GATE=1时，当计数初值写入减法计数器就开始计数），硬件启动（计数初值写入减法计数器后，等GATE由0变为1的上升沿出现才开始计数）。
停止方式：强制停止方式（对于重复计数过程，因为能自动重装载，计数过程会反复进行，不能自动停止，要停止计数必须加控制信号，方法是置GATE=0），自动停止方式（对于单次计数过程，一到计数完毕就自动停止）。
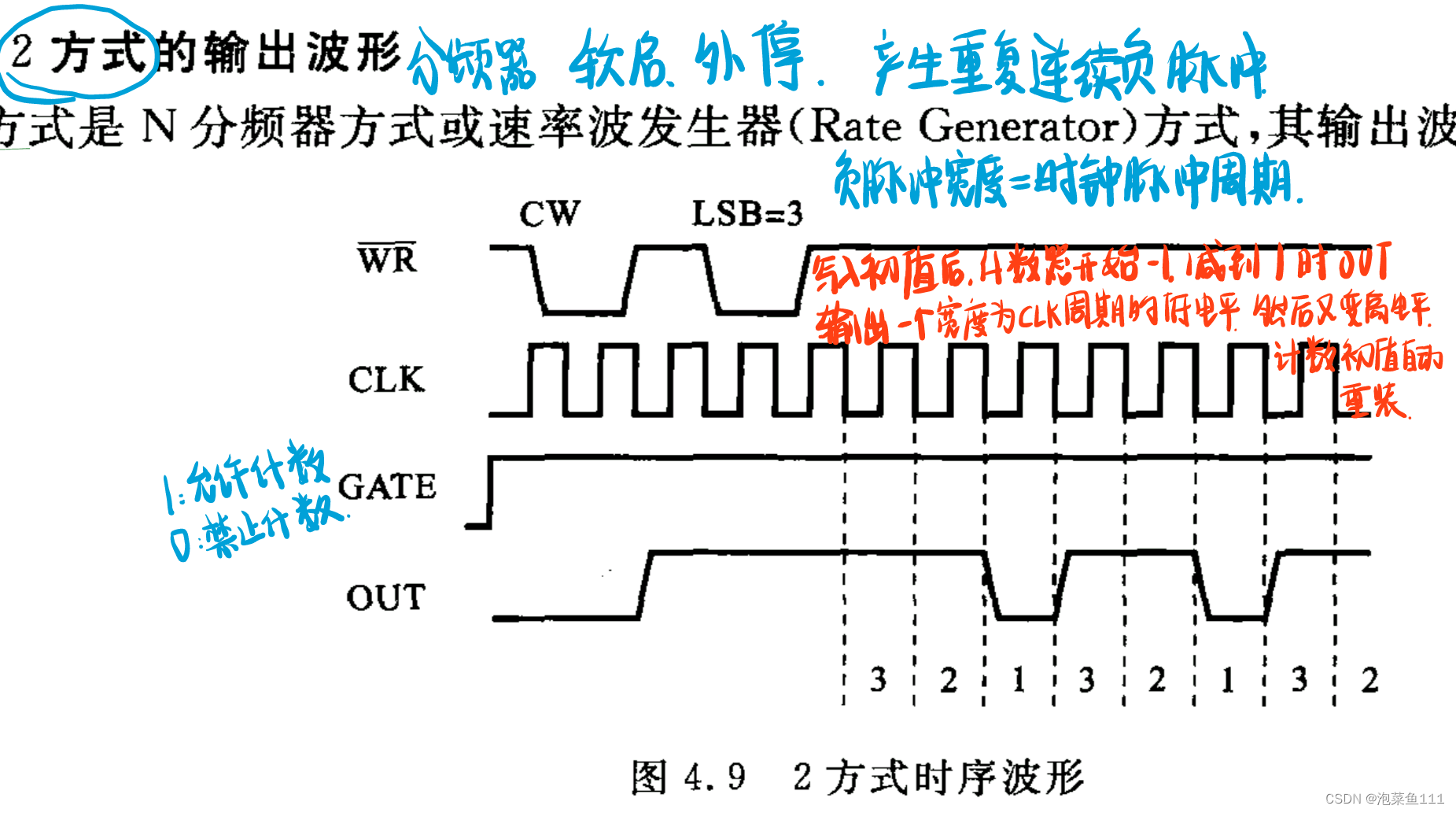
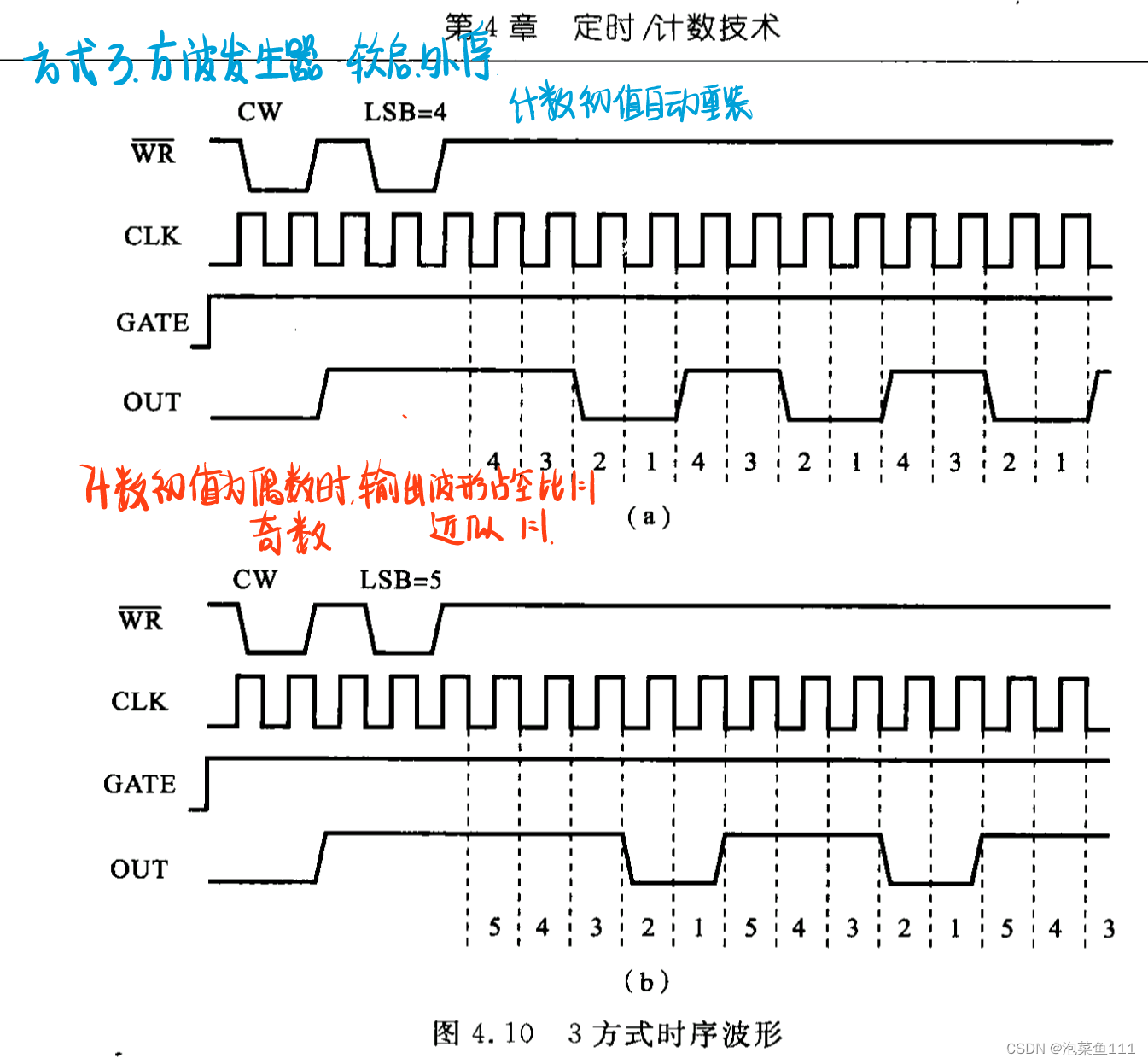
因为只有方式2和方式3有自动重装载功能，所以只有方式2和方式3能输出连续波形，其他方式只能输出单次波形。
方式0： 软启 自动结束
方式1：硬启 自动结束
方式2：软启 不自动结束
方式3：软启 不自动结束
方式4：软启 自动结束
方式5：硬启 自动结束
计数初值的计算与装入
作计数器用：次数就是计数初值，直接装入就可，不用换算。
作定时器用：需要换算，换算方法：
装入：16位减法计数器，8253外部数据线只有8位，所以先装低八位，后装高八位，写入同一个端口。
8253的初始化
