MDK5插件以及主题应用
- 前言
- 一、主题修改
- 1、主题文件下载
- 2、主题应用
- 二、插件安装以及使用
- 1.下载插件
- 2、插件使用步骤
前言
为了写代码的心应手,先对MDK5进行改造
提示:以下是本篇文章正文内容,下面案例可供参考
🎉参考了其他大师的文章,链接如下:
MDK5插件:代码格式整理、文件注释、函数注释
一、主题修改
1、主题文件下载
主题文件下载链接
2、主题应用
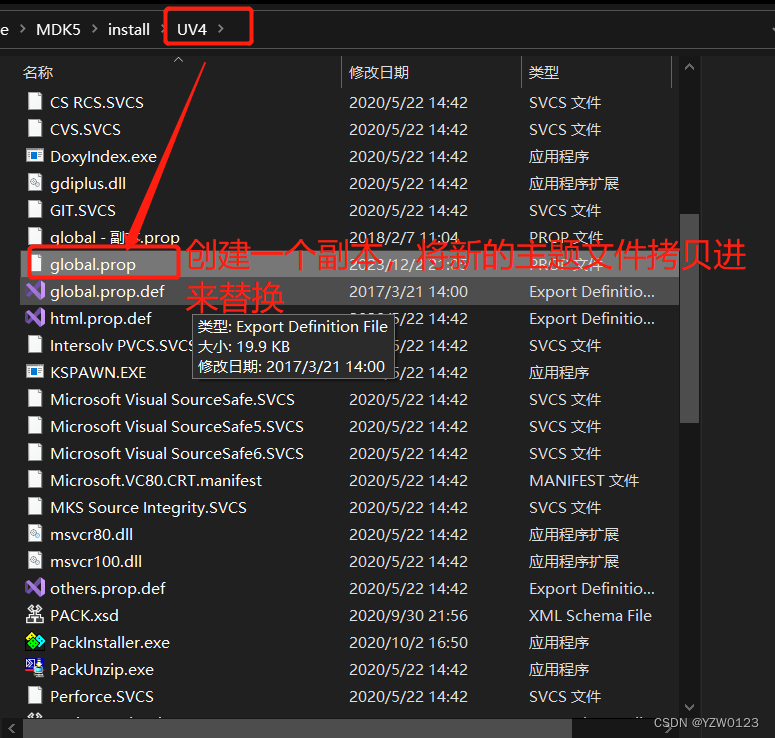
在MDK的安装目录下找到global.prop文件(创建一个副本主题文件有问题时恢复防止软件崩了),并将新的主题文件复制过来替换。
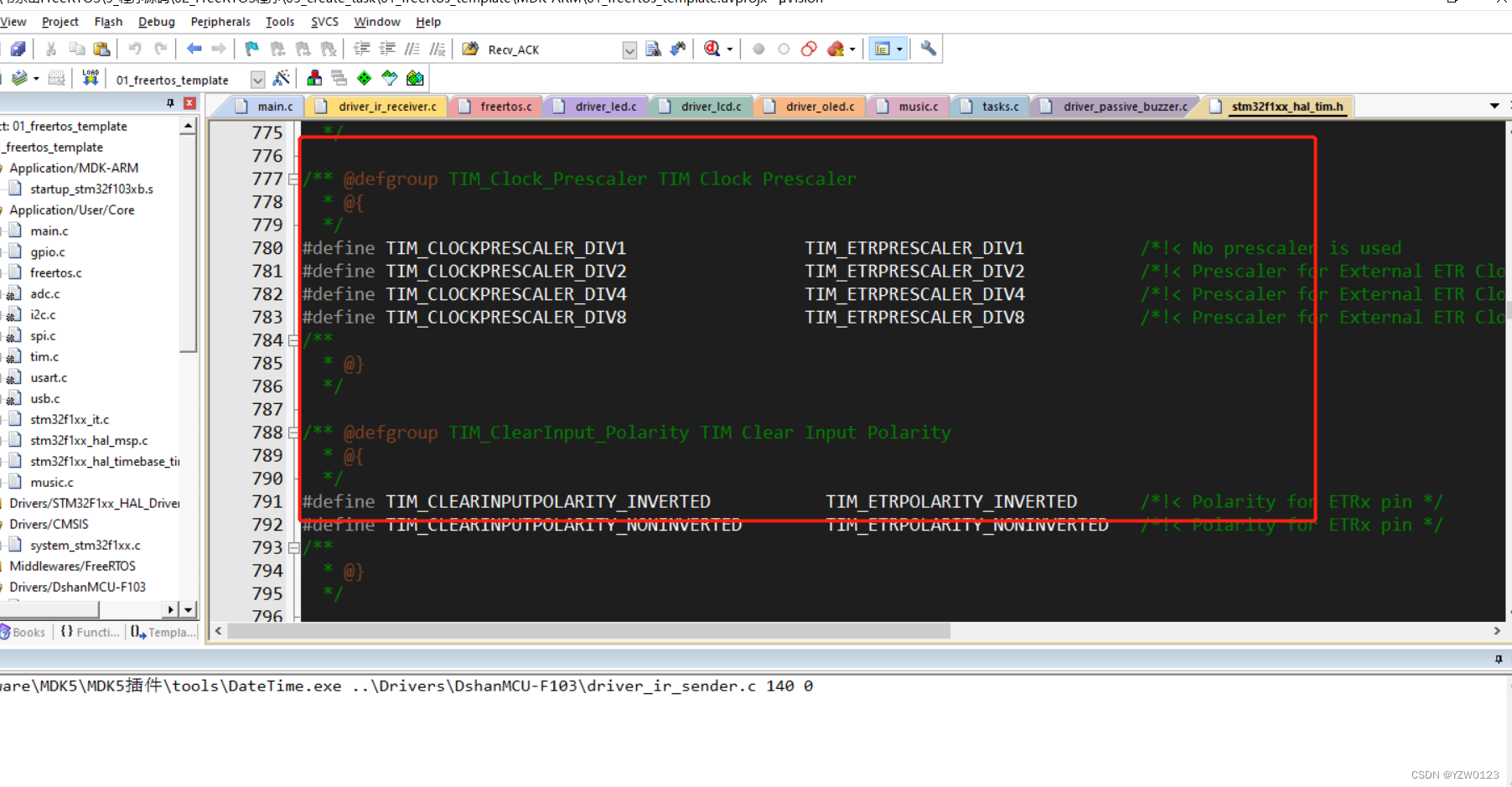
 重启之后可以看到主题效果如下,另外可以在网上多找一些主题文件看看哪个适合自己。
重启之后可以看到主题效果如下,另外可以在网上多找一些主题文件看看哪个适合自己。
二、插件安装以及使用
1.下载插件
插件下载地址
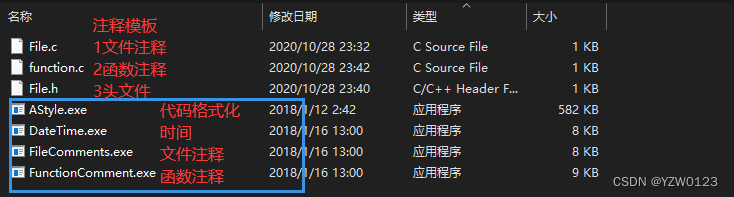
2、插件使用步骤
在MDK5中按照下图步骤设置插件使用方法以及快捷键设置
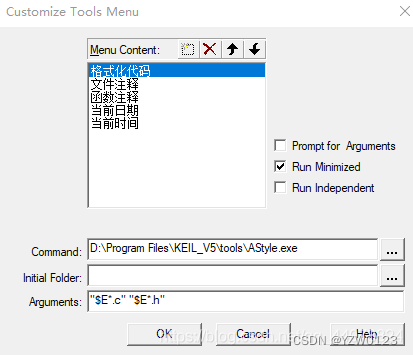
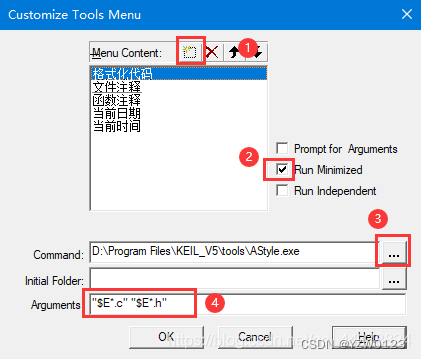
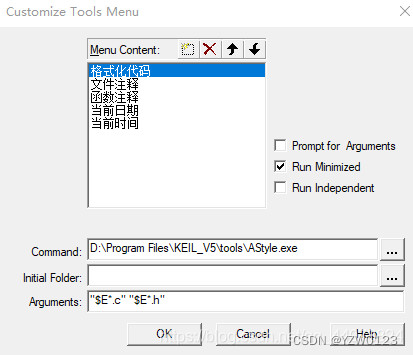
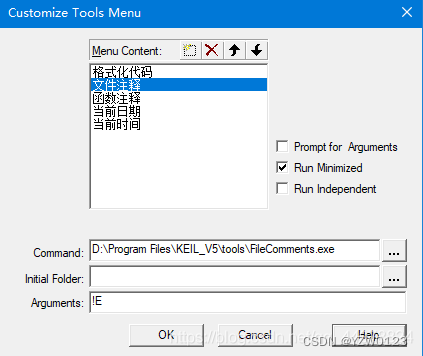
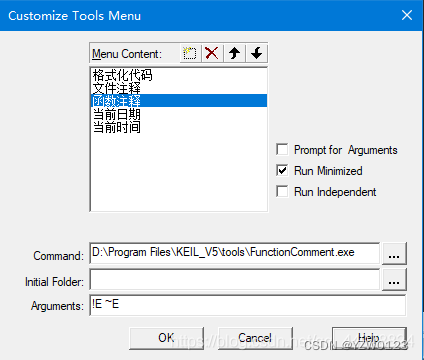
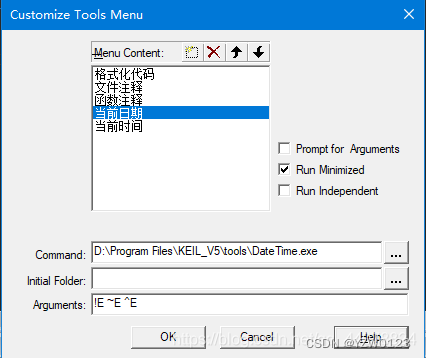
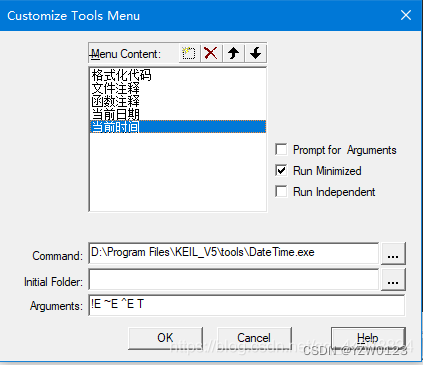
快捷键设置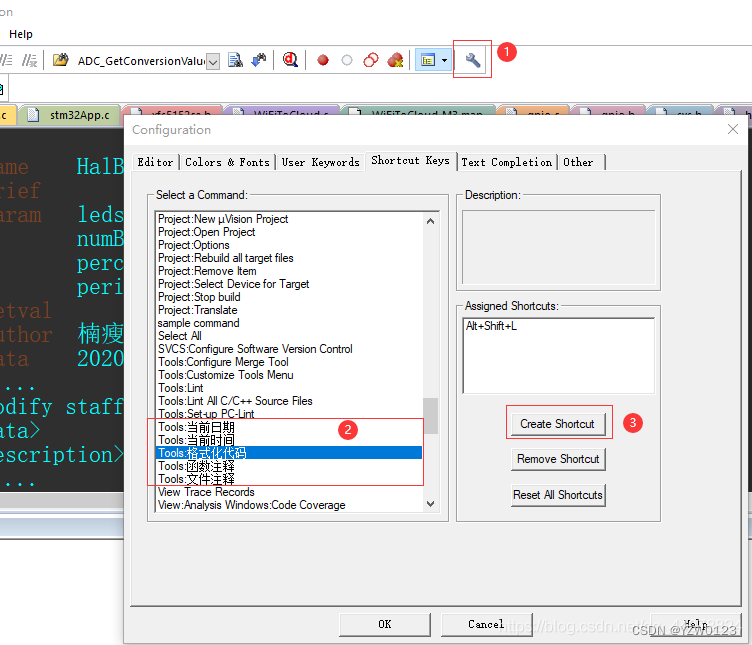






和 int(10)区别)



】)

找出1-99之间的全部同构数)






