文章目录
- 一、基本问题
- 二、三个坐标系
- 三、相机标定
- 四、立体视觉
我的《计算机视觉》系列参考UC Berkeley的CS180课程,PPT可以在课程主页看到。
一、基本问题
我们的最终目标是根据一系列图像构建出整个3D世界。显然,仅凭一张图像是不够的,因为不同大小的事物放在不同的距离拍出来的图像可能是一模一样的。因此,我们需要至少两张图片来理解深度。人眼就是根据双眼所见的细微差别经过大脑处理后感知深度的。
在多视角几何中,我们需要考虑下面几个问题:
- 结构:物体的真实3D坐标是多少?
- 对应关系:给定一张图片中的一个点,它在其他图片中对应哪一个点?
- 运动:给定两张或多张图片的对应点,这些图片之间的相对相机参数(平移、旋转)是多少?
“对应关系”和“运动”是先有鸡还是先有蛋的关系,知道一个就可以推出另一个。
二、三个坐标系
我们需要考虑三个坐标系:
- 世界坐标系;
- 相机坐标系;
- 图像坐标系。
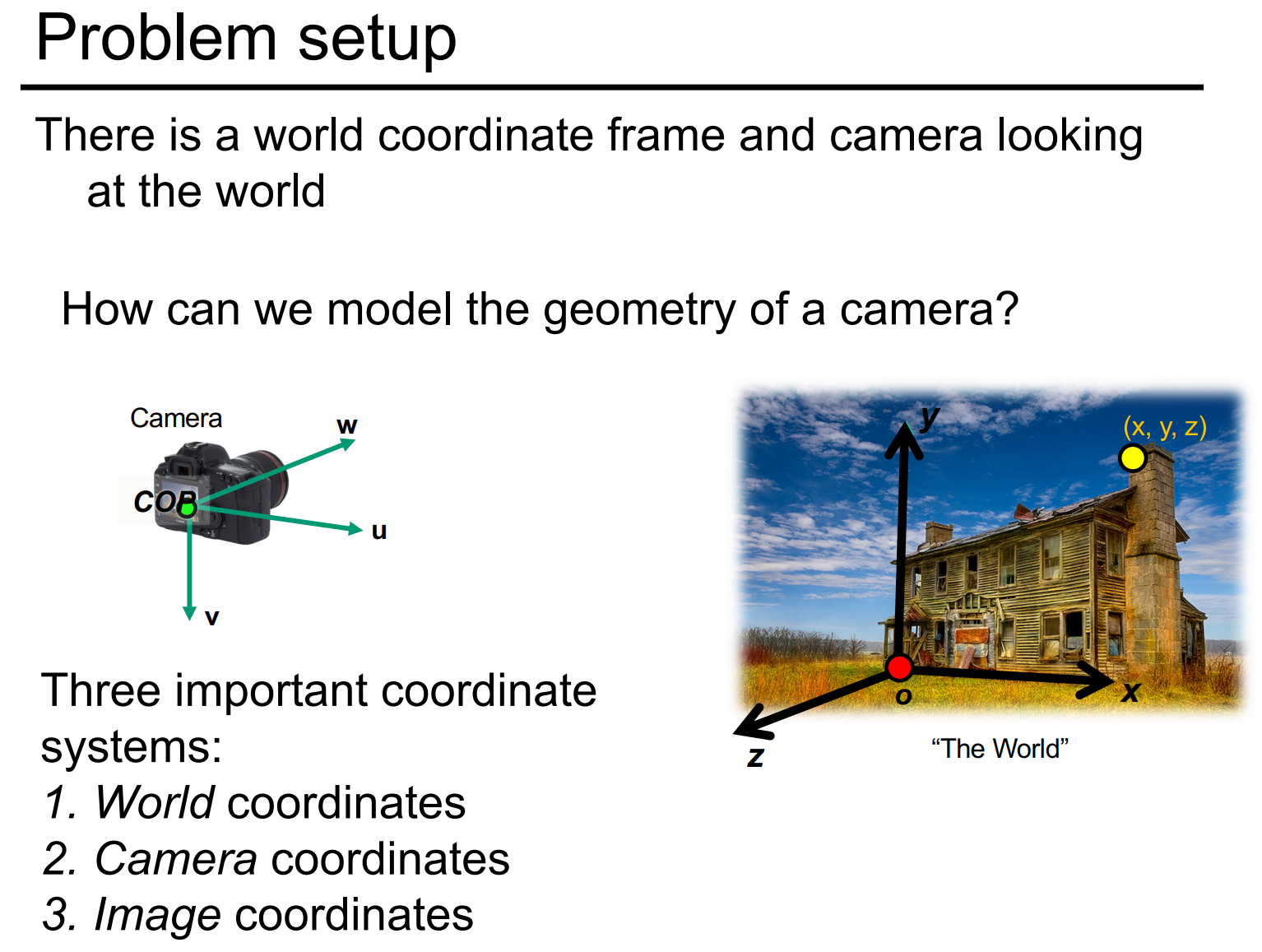
他们之间的转换关系如下图所示。
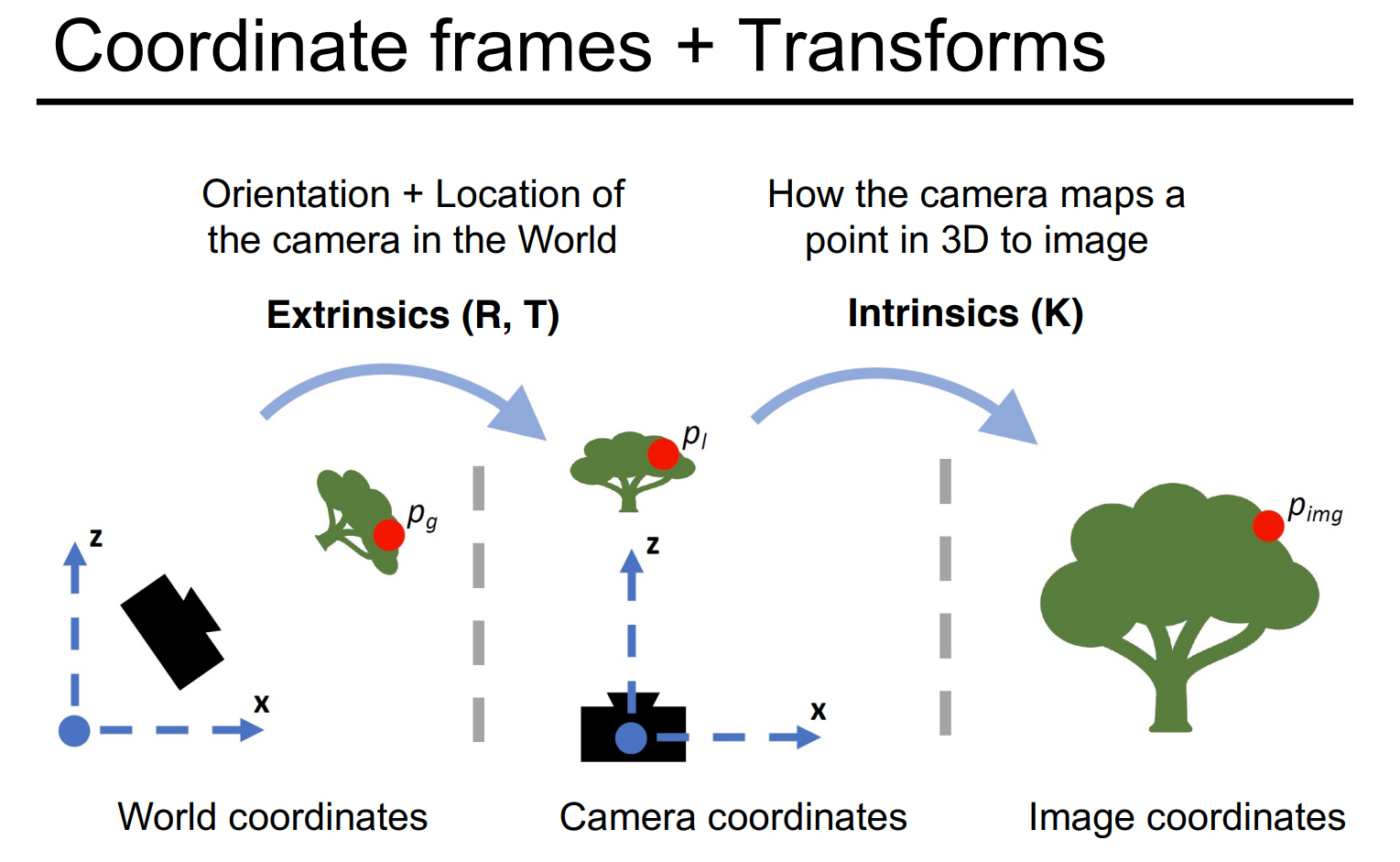
下面我们用数学语言描述这些转换关系。
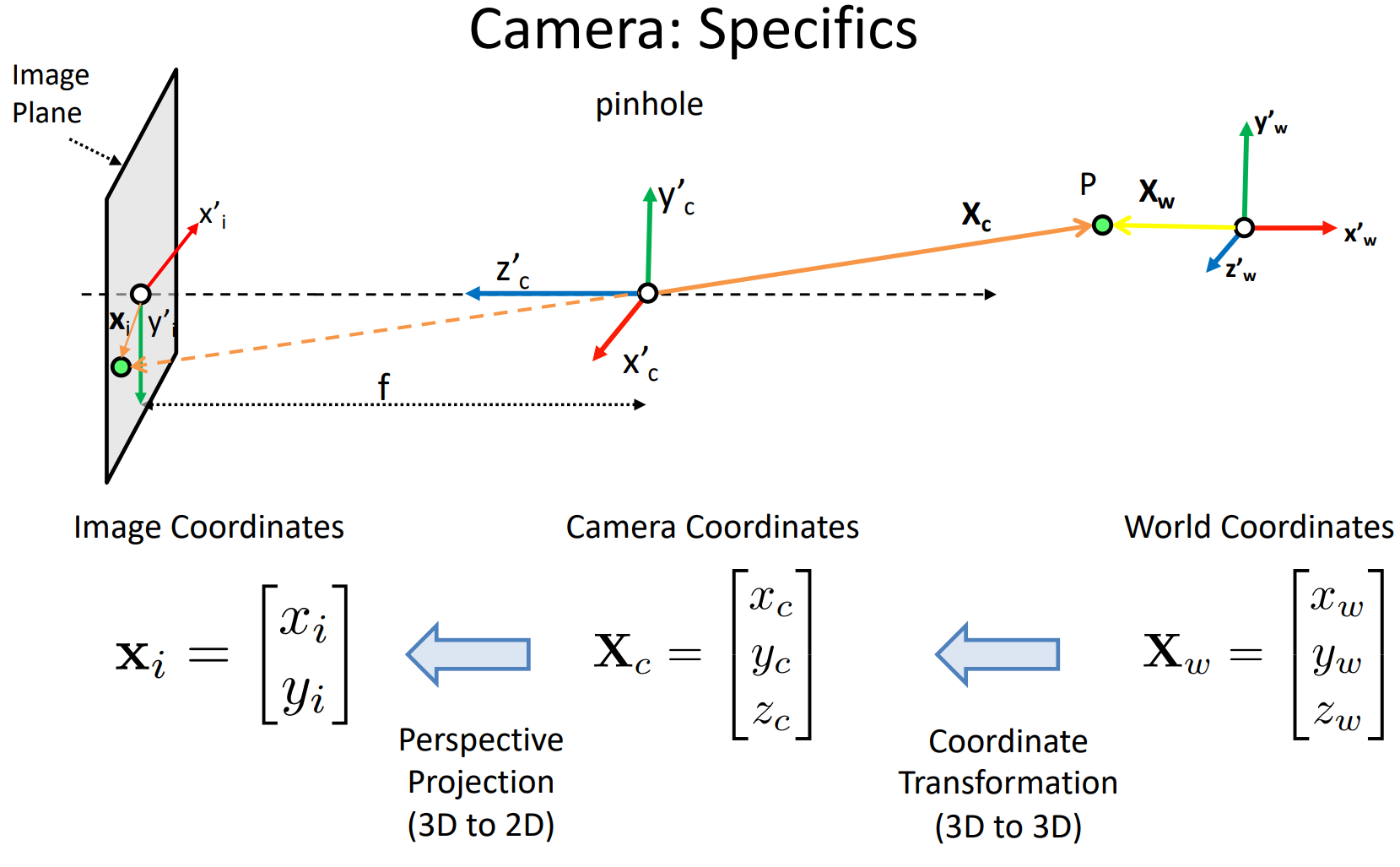
我们有世界坐标 X w = [ x w y w z w ] \boldsymbol{X}_w=\begin{bmatrix}x_w\\y_w\\z_w\\\end{bmatrix} Xw= xwywzw ,相机坐标 X c = [ x c y c z c ] \boldsymbol{X}_c=\begin{bmatrix}x_c\\y_c\\z_c\\\end{bmatrix} Xc= xcyczc (原点在光圈处),以及图像坐标 x i = [ x i y i ] \boldsymbol{x}_i=\begin{bmatrix}x_i\\y_i\end{bmatrix} xi=[xiyi]。从 X w \boldsymbol{X}_w Xw到 X c \boldsymbol{X}_c Xc的转换是3D到3D的坐标变换,从 X c \boldsymbol{X}_c Xc到 x i \boldsymbol{x}_i xi的转换是3D到2D的投影。
X w \boldsymbol{X}_w Xw到 X c \boldsymbol{X}_c Xc的转换
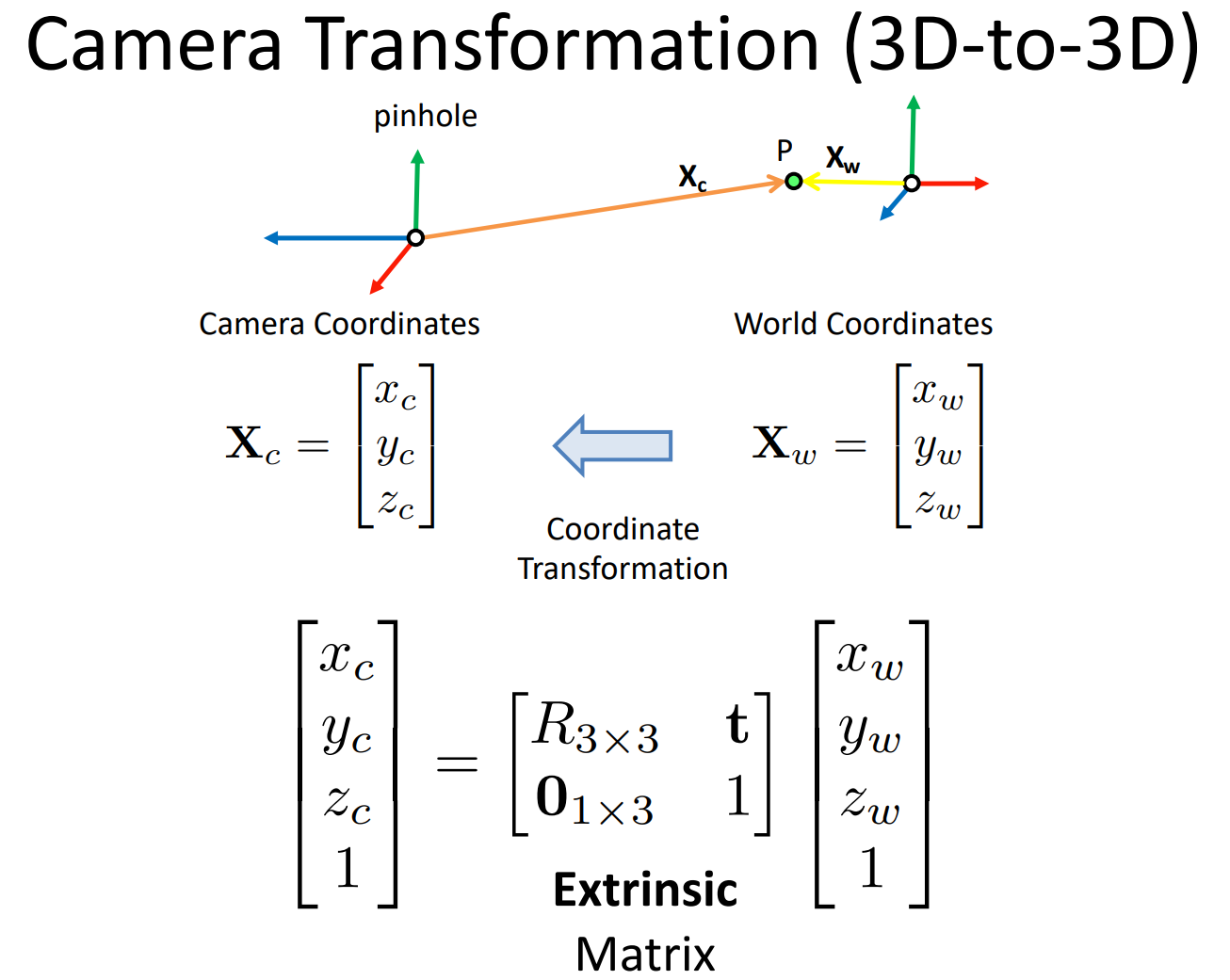
X w \boldsymbol{X}_w Xw到 X c \boldsymbol{X}_c Xc的转换是3D坐标到3D坐标的平移+旋转。一旦涉及平移,就必须使用齐次坐标(homogeneous coordinates)了——需要加一维。平移矩阵是一个 3 × 3 3\times 3 3×3的正交矩阵,向量 t \boldsymbol{t} t是一个3维的平移向量。图中的Extrinsic Matrix是两个操作的结合,它被称为相机的外参。外参共有6个自由度:3个平移自由度+3个旋转自由度(围绕各轴分别旋转)。
记Extrinsic Matrix为 T w 2 c T_{w2c} Tw2c。已知 X w \boldsymbol{X}_w Xw,可以通过 X c = T w 2 c X w \boldsymbol{X}_c=T_{w2c}\boldsymbol{X}_w Xc=Tw2cXw即 [ x c w c z c ] = R [ x w y w z w ] + t \begin{bmatrix}x_c\\w_c\\z_c\end{bmatrix}=R\begin{bmatrix}x_w\\y_w\\z_w\end{bmatrix}+\boldsymbol{t} xcwczc =R xwywzw +t来计算 X c \boldsymbol{X}_c Xc。已知 X c \boldsymbol{X}_c Xc,也可以通过 X w = T w 2 c − 1 X c \boldsymbol{X}_w=T_{w2c}^{-1}\boldsymbol{X}_c Xw=Tw2c−1Xc即 [ x w y w z w ] = R − 1 ( [ x c w c z c ] − t ) \begin{bmatrix}x_w\\y_w\\z_w\end{bmatrix}=R^{-1}\left(\begin{bmatrix}x_c\\w_c\\z_c\end{bmatrix}-\boldsymbol{t}\right) xwywzw =R−1 xcwczc −t 来计算 X c \boldsymbol{X}_c Xc。
X c \boldsymbol{X}_c Xc到 x i \boldsymbol{x}_i xi的转换
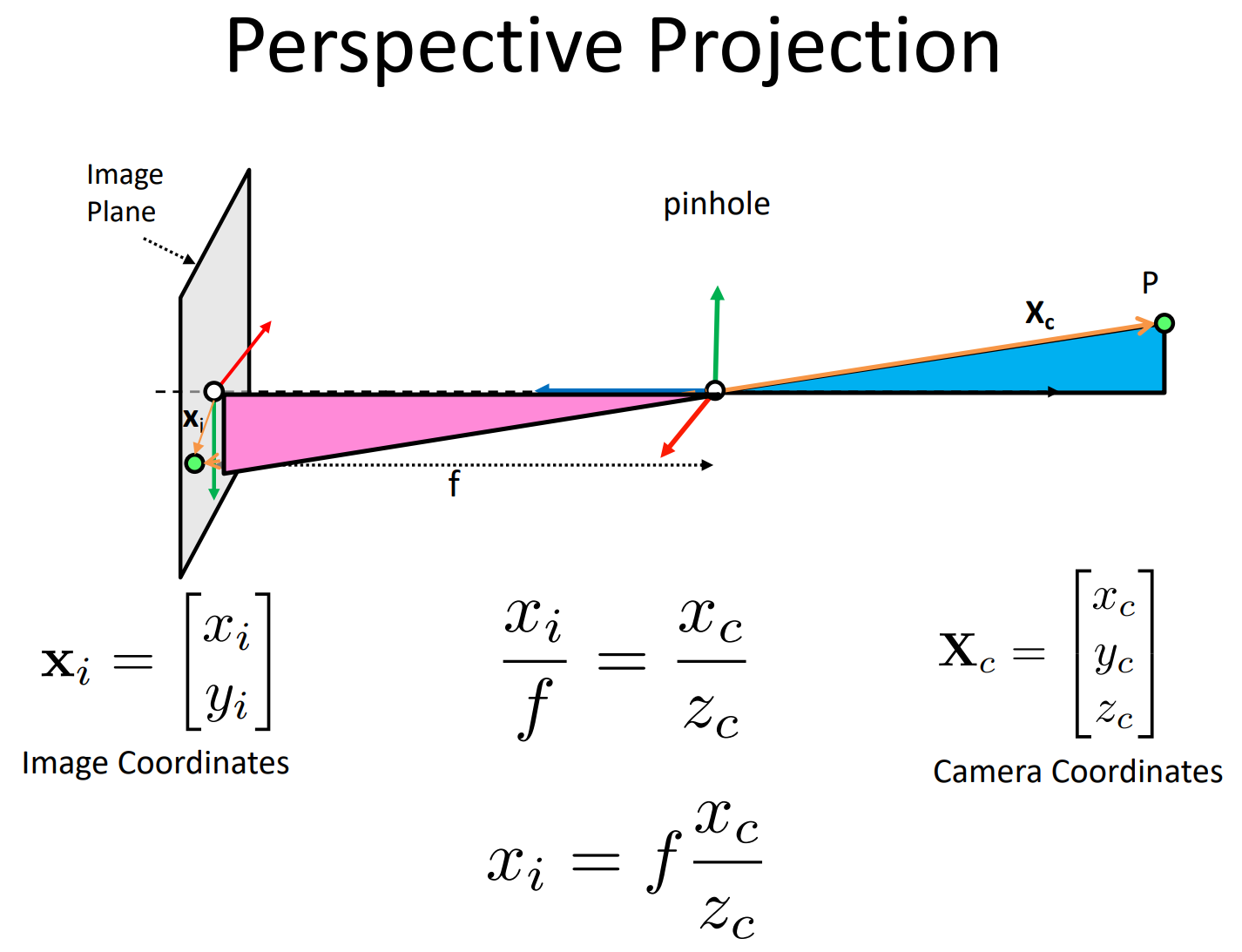
这里的情况稍复杂一些,不仅涉及相机坐标到像平面坐标的投影,还涉及到像平面坐标和最终图像坐标的对应关系。
对于相机坐标到像平面坐标的投影,我们在上一篇文章讲针孔相机的时候已经推过一个式子,这里我们就不必考虑负号了,直接写出 x i = f x c z c y i = f y c z c x_i=f\cfrac{x_c}{z_c}\\ y_i=f\cfrac{y_c}{z_c} xi=fzcxcyi=fzcyc这里假设相机坐标系的 z z z轴和像平面垂直。
此外还有像平面到图像传感器(即图像本身)的对应关系。假设像平面的度量单位是毫米,图像的度量单位是像素,那么就存在这两种单位之间的转化关系;有时水平和竖直方向上像素密度还不一样(横纵比不是1:1),所以需要两个值 m x , m y m_x,m_y mx,my来描述这种密度。像平面的原点往往对应图像的中心,即 ( 0 , 0 ) (0,0) (0,0)不一定对应 ( 0 , 0 ) (0,0) (0,0),所以还需要有一个平移 ( o x , o y ) (o_x,o_y) (ox,oy)。设图像的坐标(单位:像素)为 [ u i v i ] \begin{bmatrix}u_i\\v_i\end{bmatrix} [uivi],则 u i = m x x i + o x = f x x c z c + o x v i = m y y i + o y = f y y c z c + o y u_i=m_x x_i+o_x=f_x \frac{x_c}{z_c}+o_x\\ v_i=m_y y_i+o_y=f_y \frac{y_c}{z_c}+o_y ui=mxxi+ox=fxzcxc+oxvi=myyi+oy=fyzcyc+oy其中 f x = m x f f_x=m_x f fx=mxf, f y = m y f f_y=m_y f fy=myf。我们想要把这个关系表示成矩阵乘法,但是矩阵乘法无法描述除法,所以又要用到齐次坐标。我们知道,齐次坐标 ( x , y , w ) T (x,y,w)^T (x,y,w)T等价于二维坐标 ( x w , y w ) T \left(\cfrac xw, \cfrac yw\right)^T (wx,wy)T,所以我们可以用齐次坐标解决除法的问题。设 ( u i , v i ) T ≡ ( u ~ i , v ~ i , w ~ i ) T (u_i,v_i)^T\equiv (\tilde u_i, \tilde v_i, \tilde w_i)^T (ui,vi)T≡(u~i,v~i,w~i)T( ≡ \equiv ≡代表等价关系),我们只需把 w ~ i \tilde w_i w~i设置成 z c z_c zc, u ~ i \tilde u_i u~i设置成 f x x c + o x z c f_x x_c+o_x z_c fxxc+oxzc, v ~ i \tilde v_i v~i设置成 f y y c + o y z c f_y y_c+o_y z_c fyyc+oyzc即可。这样我们就得到了以下矩阵: [ u i v i ] ≡ [ u ~ i v ~ i w ~ i ] = [ f x 0 o x 0 0 f y o y 0 0 0 1 0 ] [ x c y c z c 1 ] \begin{bmatrix}u_i\\v_i\end{bmatrix}\equiv\begin{bmatrix}\tilde u_i\\\tilde v_i\\\tilde w_i\end{bmatrix}=\begin{bmatrix}f_x&0&o_x&0\\0&f_y&o_y&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix} [uivi]≡ u~iv~iw~i = fx000fy0oxoy1000 xcyczc1 如果像素不是正方形而是平行四边形,还得加一个倾斜变换(skew) s s s: K = [ f x s o x 0 0 f y o y 0 0 0 1 0 ] K=\begin{bmatrix}f_x&s&o_x&0\\0&f_y&o_y&0\\0&0&1&0\end{bmatrix} K= fx00sfy0oxoy1000 这里的 K K K就是Intrinsic Matrix,他被称为相机的内参。这样,内参 K K K就有5个自由度: f x , f y , o x , o y , s f_x,f_y,o_x,o_y,s fx,fy,ox,oy,s。
投影矩阵
把各种变换汇总在一起,就形成了投影矩阵(projection matrix)。 [ u i v i ] ≡ [ u ~ i v ~ i w ~ i ] = [ f x 0 o x 0 0 f y o y 0 0 0 1 0 ] [ R 3 × 3 t 3 × 1 0 1 × 3 1 ] ⏟ 3 × 4 投影矩阵 [ x w y w z w 1 ] \begin{bmatrix}u_i\\v_i\end{bmatrix}\equiv\begin{bmatrix}\tilde u_i\\\tilde v_i\\\tilde w_i\end{bmatrix}=\underset{3\times 4\text{投影矩阵}}{\underbrace{\begin{bmatrix}f_x&0&o_x&0\\0&f_y&o_y&0\\0&0&1&0\end{bmatrix}\begin{bmatrix}R_{3\times 3}&\boldsymbol{t}_{3\times 1}\\\boldsymbol{0}_{1\times 3}&1\end{bmatrix}}}\begin{bmatrix}x_w\\y_w\\z_w\\1\end{bmatrix} [uivi]≡ u~iv~iw~i =3×4投影矩阵 fx000fy0oxoy1000 [R3×301×3t3×11] xwywzw1 投影矩阵共有5+6=11个自由度。
尺度模糊问题
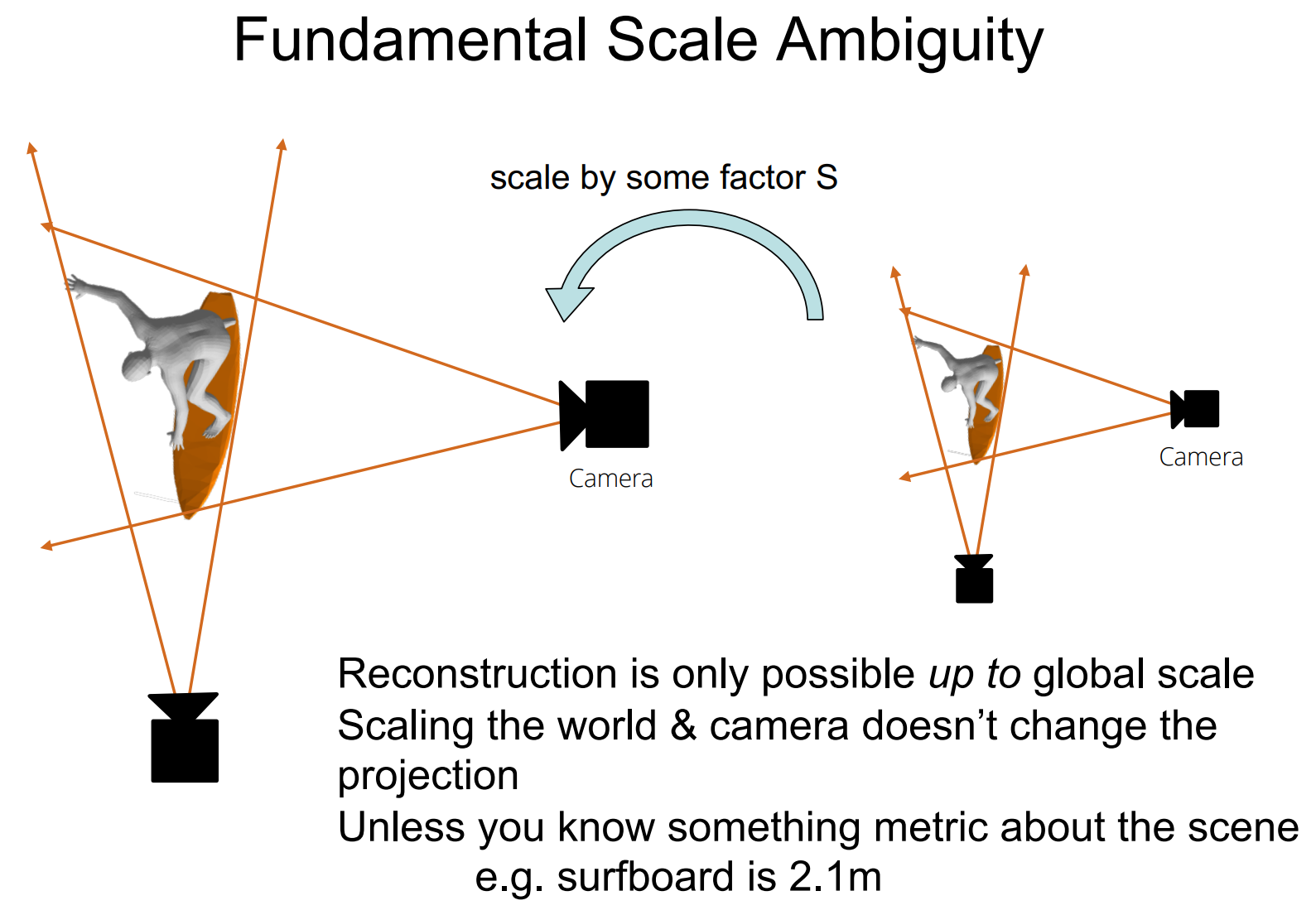
还有一个问题:如果我们把整个世界(包括相机)都放大很多倍,那么拍出来的照片仍然是一模一样的。想要从照片重建世界并且要有精确的尺度,就必须知道世界中某个物体的大小(例如图中的冲浪板是2.1m)。这也就解释了为什么投影矩阵有12个元素但是只有11个自由度。
三、相机标定
那我们如何求得相机的内外参呢?这时候就需要用到相机标定(camera calibration)。基本思路是知道世界中一些物体的3D坐标以及它们在图片上的坐标,通过线性回归(最小二乘法)拟合出投影矩阵。

虽然是拟合矩阵,但也可以转化为一般的多元线性回归问题:
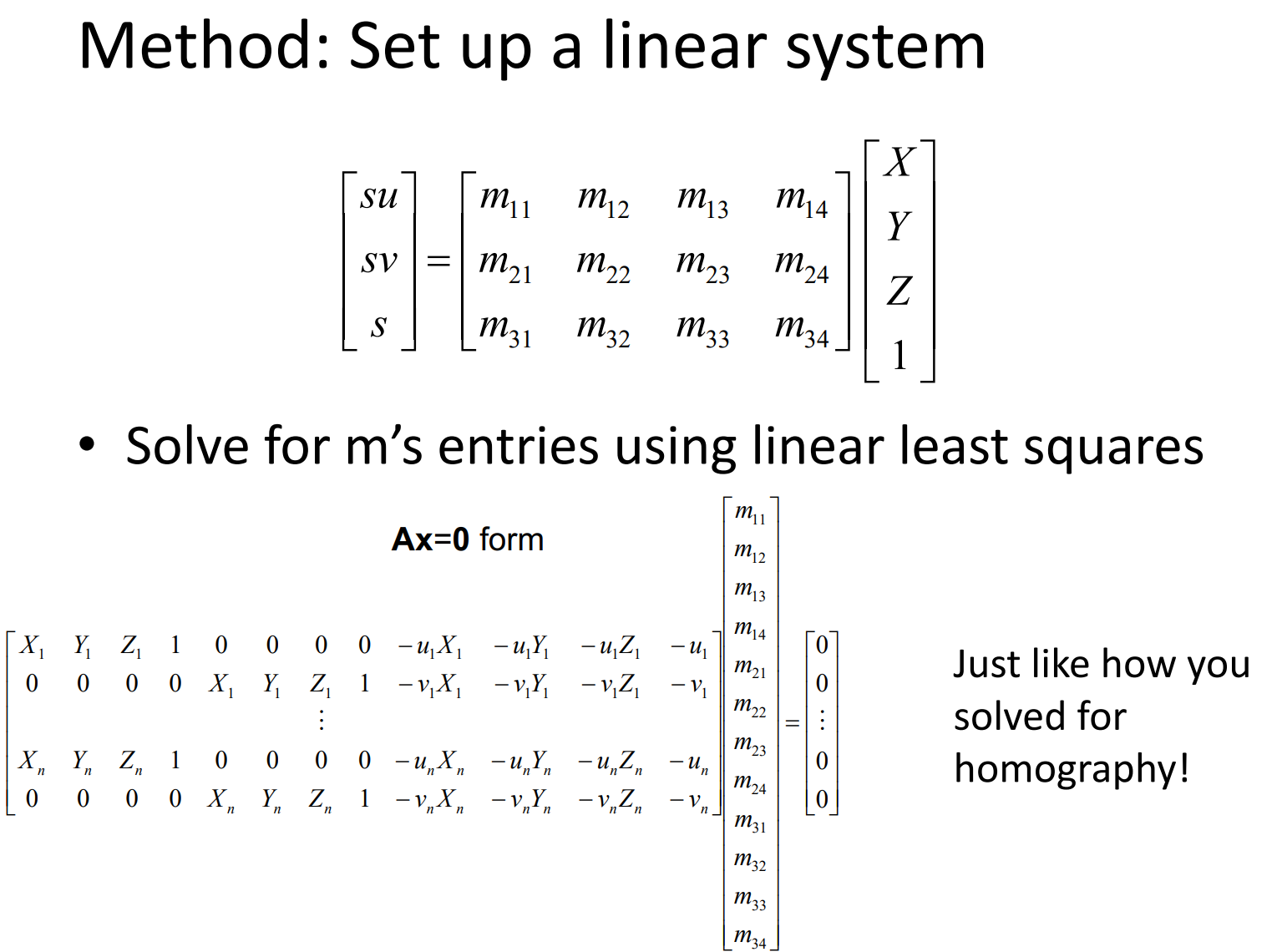
用最小二乘法就可以求出投影矩阵了。知道了投影矩阵,能不能分别求出内外参呢?答案是可以的。注意到内参 K K K只有前三列有非零元,所以令前三列为 U U U,将 K K K分块为 K = [ U 3 × 3 ∣ 0 3 × 1 ] K=[U_{3\times 3}|\boldsymbol{0}_{3\times 1}] K=[U3×3∣03×1]。这样再和外参 [ R 3 × 3 t 3 × 1 0 1 × 3 1 ] \begin{bmatrix}R_{3\times 3}&\boldsymbol{t}_{3\times 1}\\\boldsymbol{0}_{1\times 3}&1\end{bmatrix} [R3×301×3t3×11]相乘就得到了 U [ R ∣ t ] + 0 [ 0 ∣ 1 ] = U [ R ∣ t ] U[R|\boldsymbol{t}]+\boldsymbol{0}[\boldsymbol{0}|1]=U[R|\boldsymbol{t}] U[R∣t]+0[0∣1]=U[R∣t]。注意 R R R是一个正交矩阵, U U U是一个上三角矩阵,所以可以对投影矩阵的前三列进行QR分解(用格拉姆-施密特正交化方法就可以完成),从而求得 U U U和 R R R,再对投影矩阵的第四列左乘 U − 1 U^{-1} U−1即可得到 t \boldsymbol{t} t。
四、立体视觉
从 X c \boldsymbol{X}_c Xc到 x i \boldsymbol{x}_i xi,可以用内参矩阵 K K K乘以 X c \boldsymbol{X}_c Xc算出来。但是反着来呢?知道图像上的点,能不能知道它在相机坐标系对应哪个点呢?不能,因为只知道两个坐标( u i , v i u_i,v_i ui,vi),是不能求出三个坐标的。相机坐标系里一条直线上的所有点都对应像平面上的一个点。
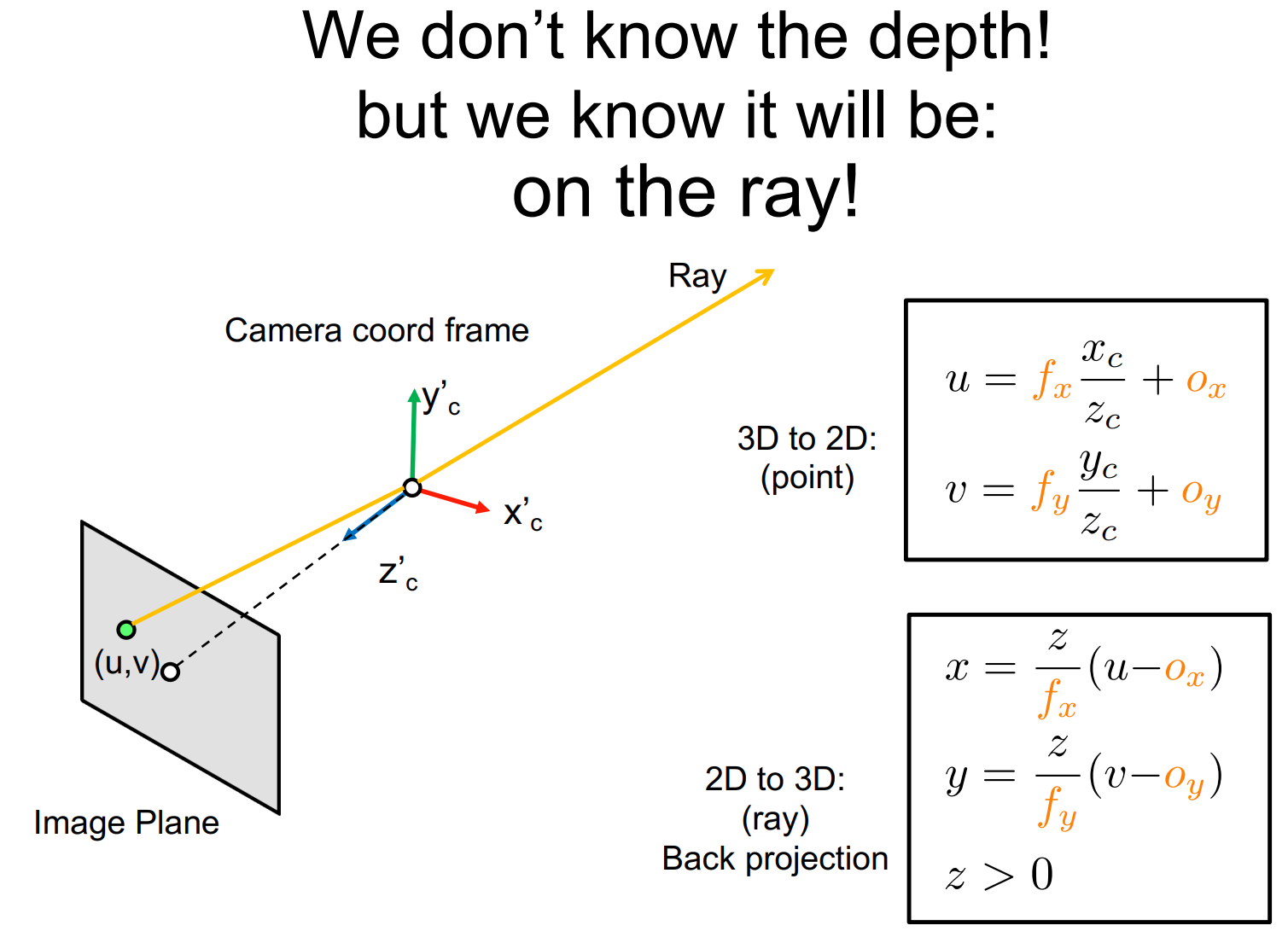
通过图中的公式可以看出,从2D到3D只能得到一条直线,该直线可以表达为关于 z z z的参数方程,但是 z z z可以取任意正数。
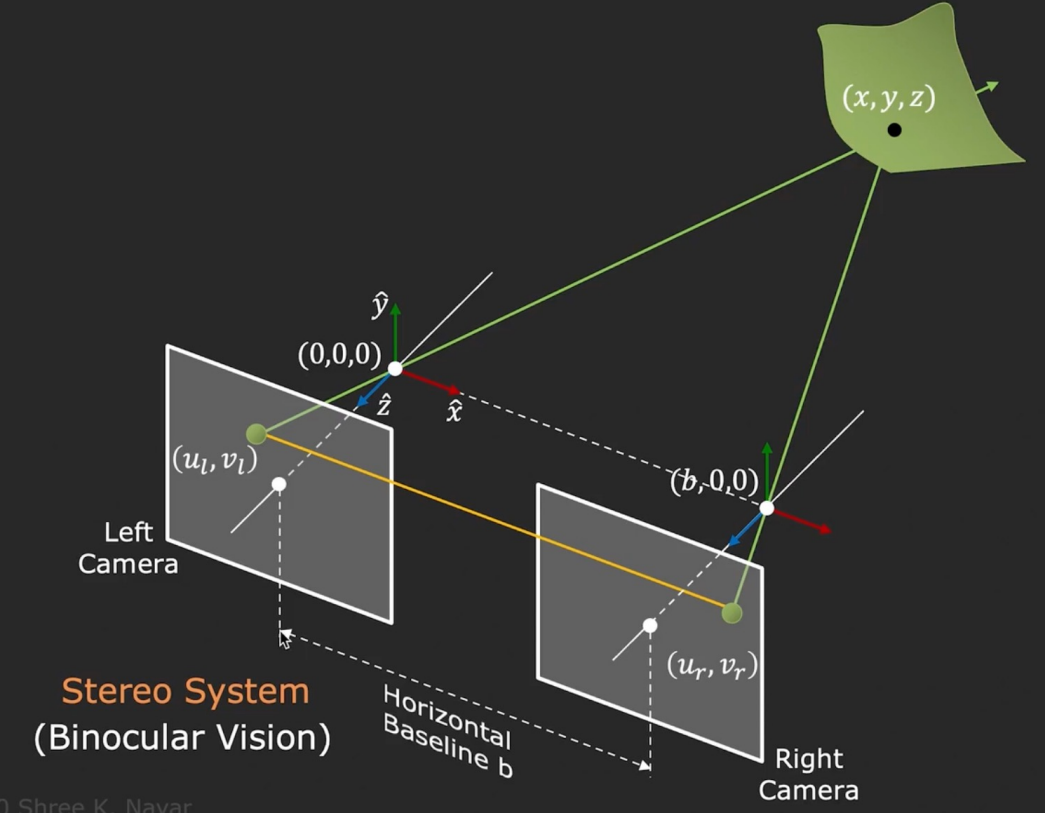
那么怎么得到深度 z z z的确切值呢?这时候就需要两张或以上的照片了。人眼的工作方式就是如此。我们先考虑最简单的情况:拍摄两张照片的两个相机光轴是平行的(相当于两个相机的像平面共面)。知道了相机之间的距离,相机的焦距,以及景物的同一个点分别对应在两张照片上的坐标,就可以用相似三角形求解出深度 z z z了:
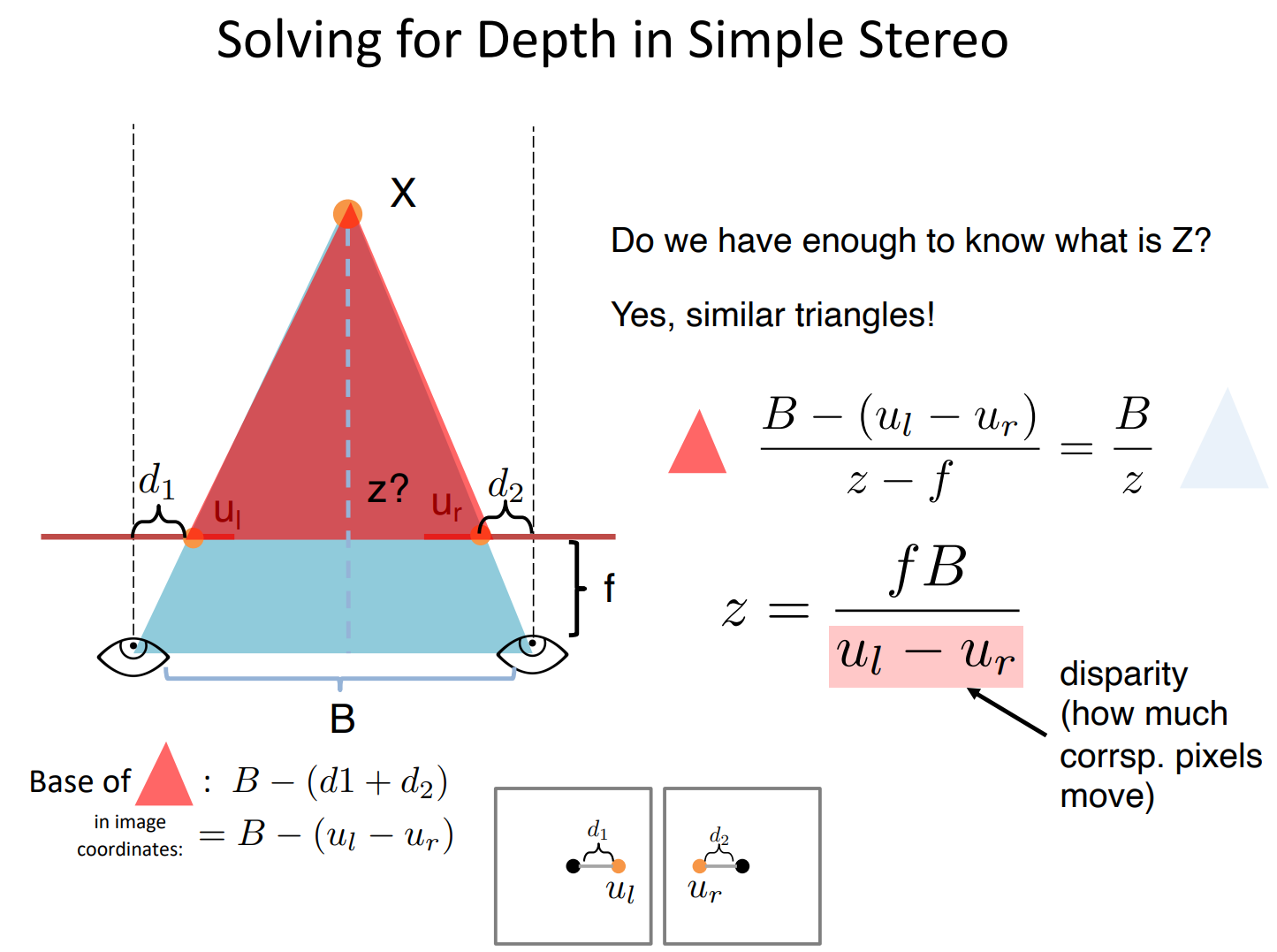
也就是说,相机移动一定距离的情况下景物在照片中移动距离的多少可以为景物的深度提供信息。移动的越多,说明景物离相机越近;反之越远。比如开车时看见路边的树在动,但是太阳却不动。深度与移动的距离成反比。
那么我们怎么自动求出景物在图片中移动的距离呢?也就是说,给定一张图片中的一点,如何求出它在另一张图片中对应哪个点呢?此时我们不知道景物的深度,但景物在第一张图片中的坐标使得我们能够确定景物在某一条直线上。景物在另一个相机(眼睛)的像平面上的坐标是由 该相机的投影中心到景物的射线 与 其像平面 的交点决定的。假设从第一个相机的投影中心到到景物的射线为 l 1 l_1 l1(左图中左边的黄线),第二个相机……的射线为 l 2 l_2 l2(左图中右边的黄线),两个相机/眼睛投影中心之间的直线为 l 3 l_3 l3,则 l 2 l_2 l2与 l 1 l_1 l1和 l 3 l_3 l3都有交点,说明 l 2 l_2 l2在由 l 1 l_1 l1和 l 3 l_3 l3确定的平面 P P P上。不论景物深度如何,从第二个相机到景物的射线(图中的多条蓝线)与第二个相机像平面的交点总是在平面 P P P上,也就是在平面 P P P和像平面的交线上。因此景物在第二张图片中可能出现的位置一定是一条水平的直线。
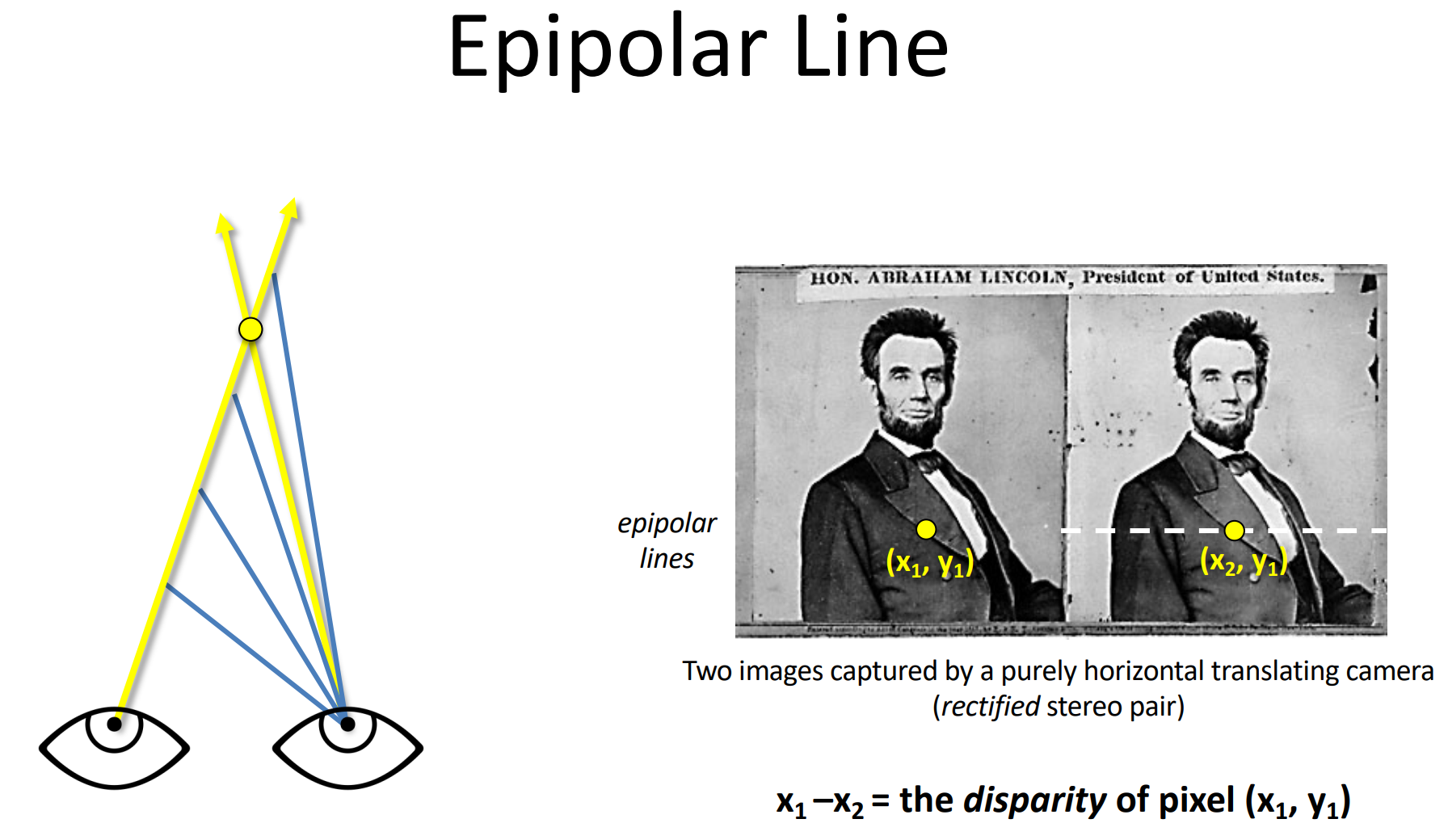
因此我们只需要在第二张图片的那一条水平线上搜索就可以了( y y y与第一张图片一致,只枚举 x x x)。我们可以考虑一个滑动的小窗口,其中心在那条水平线上,与第一张图片景物对应点周围的窗口匹配,匹配度用归一化互相关(Normalized Cross Correlationn, NCC)来计算。我们希望窗口足够大,使得亮度有明显的变化;我们也希望窗口足够小,使得窗口中尽量不包含多个深度的景物。不过,这种方法能够奏效,景物必须有不重复的纹理(白墙、花纹重复的地毯就是大坑);而且近大远小也是一种阻碍,在它的影响下窗口在第二张图片中会有所变形。


)




![[动态规划] (二) LeetCode 面试题 08.01.三步问题](http://pic.xiahunao.cn/[动态规划] (二) LeetCode 面试题 08.01.三步问题)






)



之basename)

