[动态规划] (二) LeetCode 面试题 08.01.三步问题

面试题 08.01. 三步问题

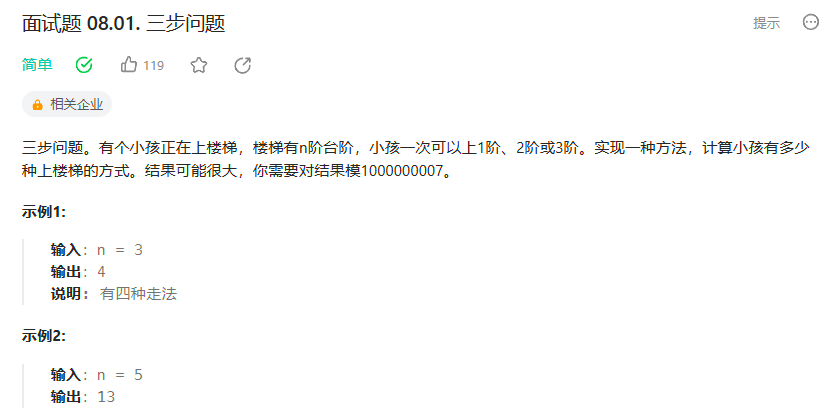
题意解析

(1) 小孩可以跳1-3阶台阶

(2) 结果很大，结果取模1000000007

解题思路

1.状态表示

dp[i]：跳到第i阶台阶有多少种方法。

2.状态转移方程

从第0阶到第1阶的方法有：1种

第0阶到第1阶(0-1)

从第0阶到第2阶的方法有：1+1 = 2种

第0阶到第一阶到第二阶(0-1-2) 和 第0阶到第2阶(0-2)

从第0阶到第3阶的方法有：1 + (1+1) + 1 = 4种

第一种分类：0-1-3

第二种分类：0-1-2-3 、 0-2-3 和 0-3

从第0阶到第4阶的方法有：1 + 2 + 4 = 7种

第一种分类：0-1-4

第二种分类： 0-1-2-4 和 0-2-4

以及第三种分类：0-1-3-4 、0-1-2-3-4、0-2-3-4 和 0-3-4

我们已经可以发现第n种就是对前3种方法的累加和。

…

从第0阶到第n阶的方法有：

(因为小孩仅能走1步、2步和3步，所以仅和n-1 、n-2 、n-3有关)

• dp[n-1] -> n：dp[n-1]种
• dp[n-2] -> n：dp[n-2]种
• dp[n-3] -> n： dp[n-3]种

即dp[n] = dp[n-1] + dp[n-2] + dp[n-3] 种

所得状态转移方程为：

dp[i] = dp[i-1] + dp[i-2] + dp[i-3]

3.初始化和填表顺序

初始化：

dp[1] = 1, dp[2] = 2, dp[3] = 4

填表顺序：

从左到右

4.返回值

题意：到第n位置的方法。

dp[i]：跳到第i阶台阶有多少种方法。

return dp[n];

请先尝试书写代码，再来看后面的内容。

---

代码实现

class Solution {
public:int waysToStep(int n) {//0 1 2 3; 1:0-1; 2:0-1-2, 0-2; 3:0-1-3 0-1-2-3 0-2-3 0-3;//处理边界情况if(n <= 2) return n;else if(n == 3) return 4;//创建dp表vector<long long> dp(n+1);//初始化dp数组dp[1] = 1, dp[2] = 2, dp[3] = 4;for(int i = 4; i <= n; i++){//填表dp[i] = (dp[i-1] + dp[i-2] + dp[i-3]) % 1000000007;}return dp[n];}
};

总结

细节1：处理边界情况。(很简单不多说)

细节2：遍历完整的n, i <= n。

细节3：题目要求对结果%1000000007，我们在相加后直接取模，防止数据太大。