1. 圆周率的介绍

1. 圆周率π自古就是人们计算的问题，π到底是什么，圆的周长与直径的比值或者是面积与半径的平方之比，或者是使sinx=0的最小正数x。所以每一种定义每一种理解都是对应着一种解法，每一种定义都是数学中不同门类对应着对π的理解，也就是各自门类的解法。
2. 常见的计算方法割圆术、无穷级数（拉马努金圆周率公式、BBP公式……）、其他级数（自然数倒数偶次方和、泰勒展开……）、微积分……（方法有很多我就不一一举例了，如果想要探索更多方法看这个博主写的文章就好了）

2. BBP公式计算圆周率

1. 公式
   
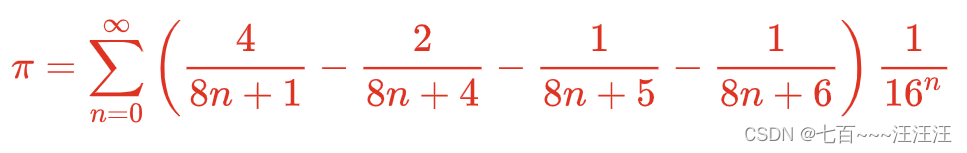
2. 证明：刚刚提到的文章（以后会更新）
3. 代码

   import mathdef  bbp_pi(digits):pi = 0for k in range(digits):term = (1 / 16**k) * ((4 / (8 * k + 1)) - (2 / (8 * k + 4)) - (1 / (8 * k + 5)) - (1 / (8 * k + 6)))pi += termreturn pi# 指定所需的小数位数
   decimal_places = 100
   calculated_pi = bbp_pi(decimal_places)print("计算得到的π值：", calculated_pi)

4. 运行结果

   计算得到的π值： 3.141592653589793
   请按任意键继续. . .
   

3. 蒙特卡洛方法计算π

1. 原理
   
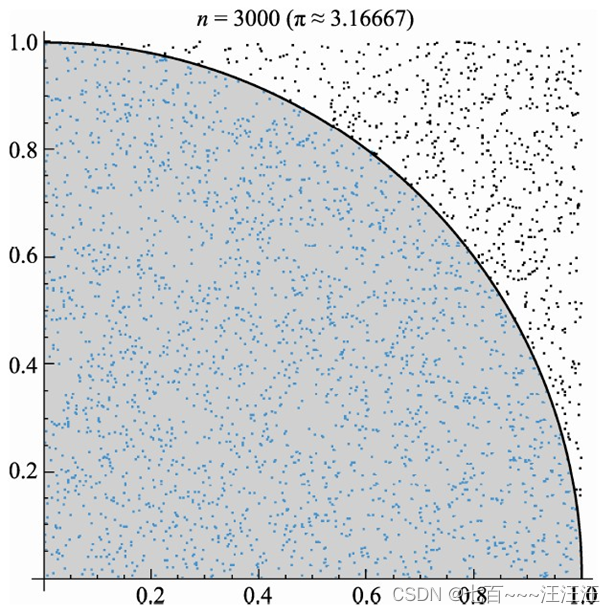
2. 代码

   from random import random
   from math import sqrt
   from time import clock
   DARTS = 1000# 一共投掷的点数
   hits = 0.0# 范围内的点数
   clock()计时
   for i in range(1, DARTS+1):x, y = random(), random()dist = sqrt(x ** 2 + y ** 2)# 计算点到圆心的距离先求横纵坐标的平方和再求算数平方根if dist <= 1.0:hits = hits + 1
   pi = 4 * (hits/DARTS)
   print("Pi值是{}.".format(pi))
   print("运行时间是: {:5.5}s".format(clock()))
   

3. 运行结果

   Pi值是3.144.
   请按任意键继续. . .