0. 内容

1. 时间戳同步问题及意义
时间戳同步的原因:如果不同步,由于IMU频率高,可能由于时间戳不同步而导致在两帧camera之间的时间内用多了或者用少了IMU的数据,且时间不同步会导致我们首尾camera和IMU数据时间不同,会使估计存在误差,使我们的系统精度下降甚至出现错误的预测。如果以IMU时间为准确的,同步之后,我们可以用时间戳偏移对系统估计的 T w b T_{wb} Twb进行补偿(思路1),或者能够得到与首尾IMU时间相同的时间对应的两帧camera的观测(思路2),提升系统精度。
时间戳同步有两种方式:硬同步和软同步。
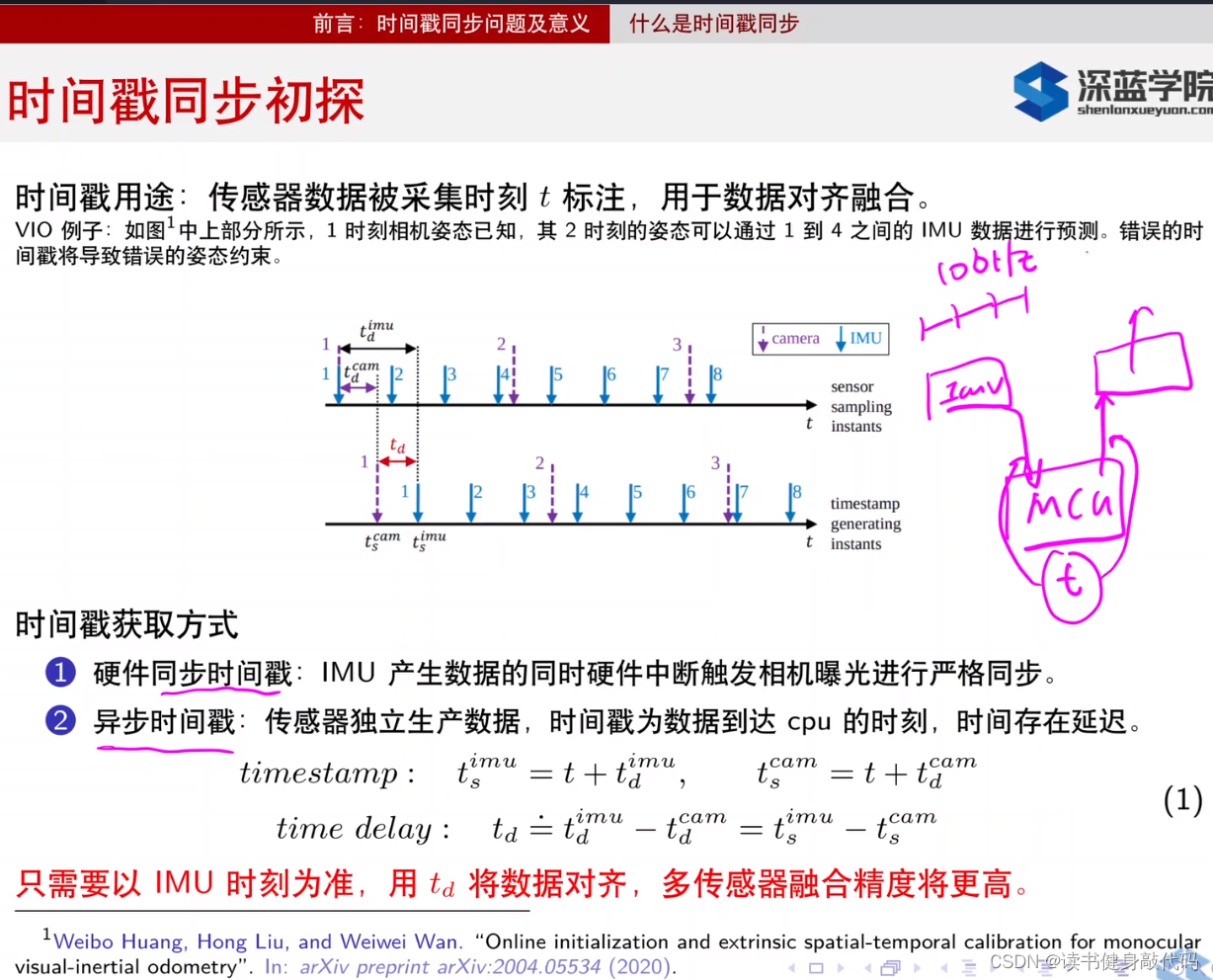
- 硬同步即硬件同步:即IMU(或其他传感器)产生数据的同时给一个信号,可用于出发MCU中断,然后触发camera曝光,使camera输出图像的时间戳本身就和IMU同步,从而实现硬件同步。
- 软同步即软件同步:在软件上对收到的IMU和camera数据进行运算,解算出时间戳。具体来说,camera和IMU从产生到到达MCU是需要时间的,这段时间分别叫 t d c a m t_d^{cam} tdcam和 t d i m u t_d^{imu} tdimu,产生时间分别加上这个时延就的到了MCU采样的时间戳,二者相减就是真正的时间戳,这里我们只需要这个时间戳的相对量,所以我们可以假设IMU是准确的, t d i m u − t d c a m t_d^{imu}-t_d^{cam} tdimu−tdcam就是我们MCU所知的时间戳偏移 t d t_d td。
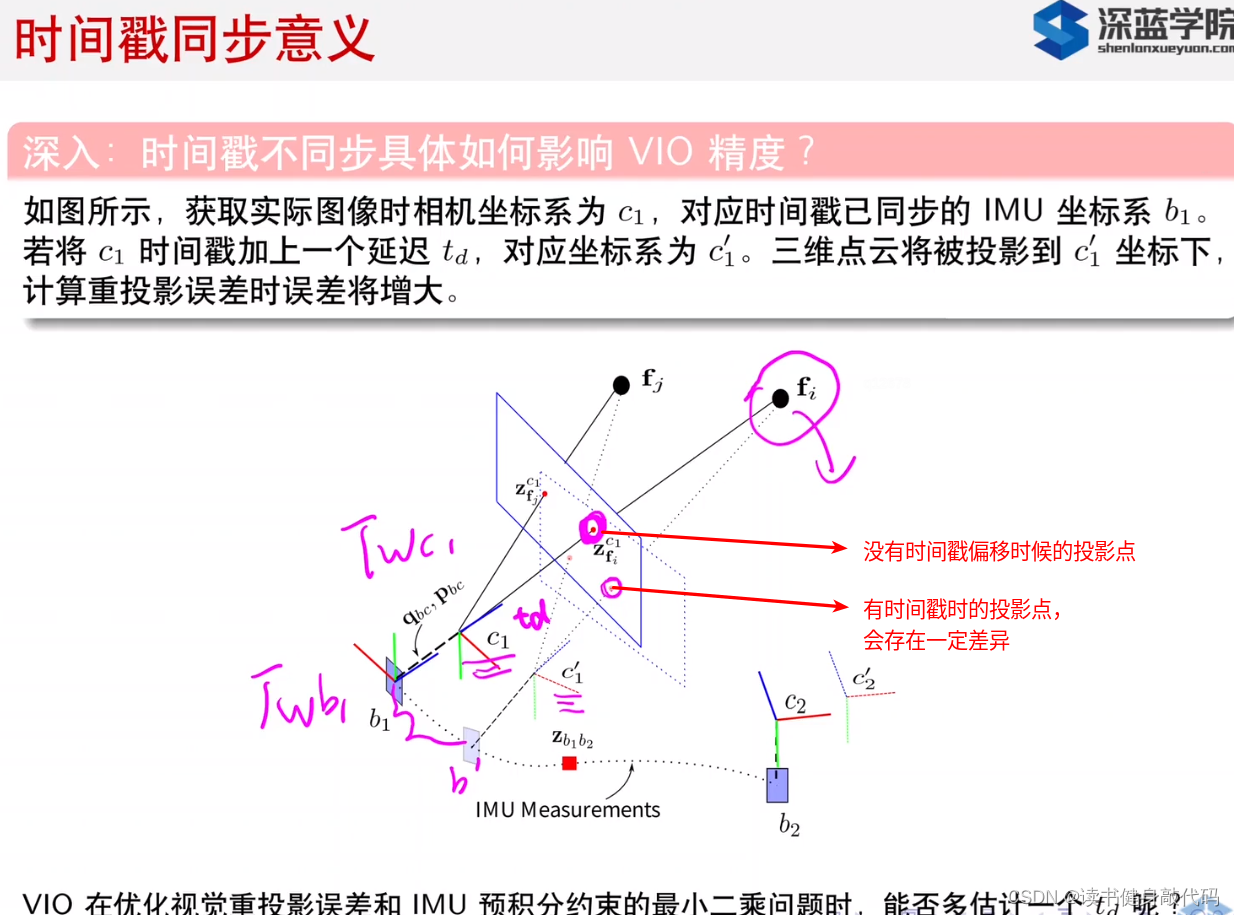
1.1 思路1:补偿camera pose的估计(轨迹匀速模型)
位姿补偿公式思路:假设相机在两帧间是匀速运动。VIO输出的是系统在world系下的pose,即 T w b T_{wb} Twb,我们需要补偿的是 T w c T_{wc} Twc,于是就结合VIO输出的角速度,速度反向推到cam时刻(补偿了 t d t_d td之后的时刻),然后再用外参 T b c T_{bc} Tbc转到cam系下即可:

在VIO残差中进行补偿:
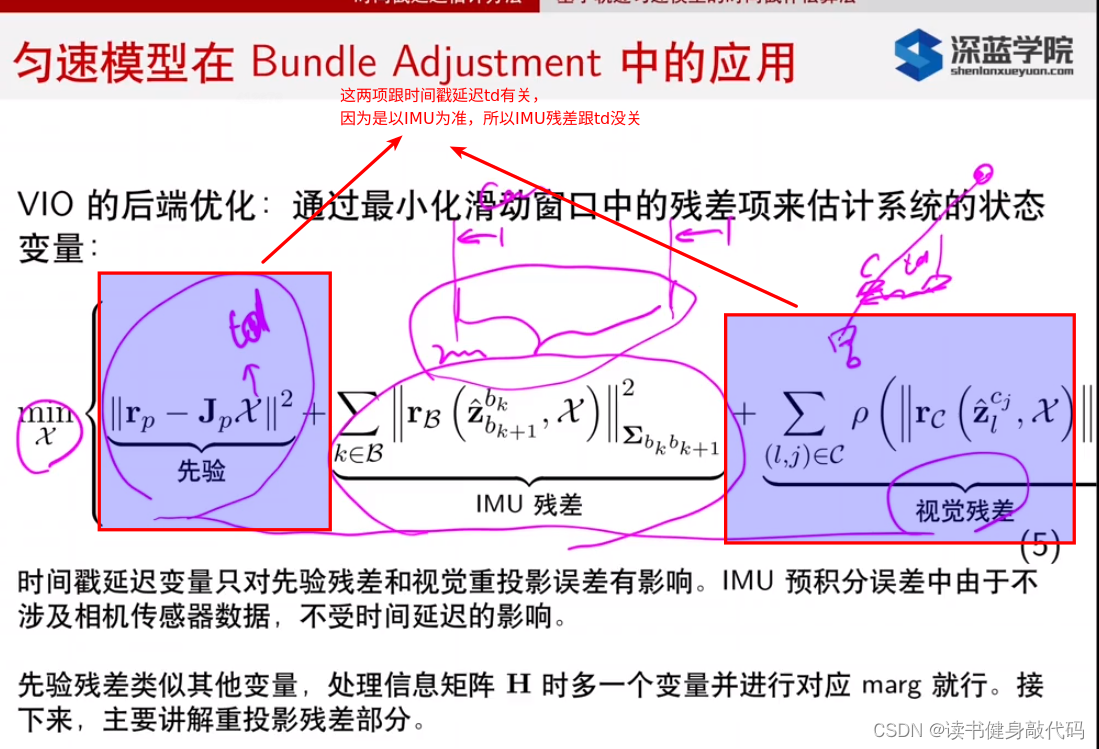

- 同样,我们VIO输出的是 T w b T_{wb} Twb所以我们要先将landmark转换到body,再转换到camera系:
- 这里实际上是在归一化平面,并没在像素平面(重投影误差的uv实际上是归一化平面的坐标,通过特征提取或者光流匹配而得),忽略了相机内参。
将式(3)带入可的式(8)
重投影误差对时间戳延时 t d t_d td的Javobian:

式(9)推导,只看中间最复杂的部分, e x p ( ω b i t d + ω b i δ t d ) exp(\omega_{b_i}t_d+\omega_{b_i}\delta t_d) exp(ωbitd+ωbiδtd),这里好理解点的话实际上角速度 ω t \omega t ωt可以写成 ( ω t ) ∧ (\omega t)^{\wedge} (ωt)∧,因为 ω t \omega t ωt可以代表一个三维的旋转矩阵,按照旋转的表达方式是轴角表示,即 旋转角度*旋转轴,可以看之前的一篇知乎
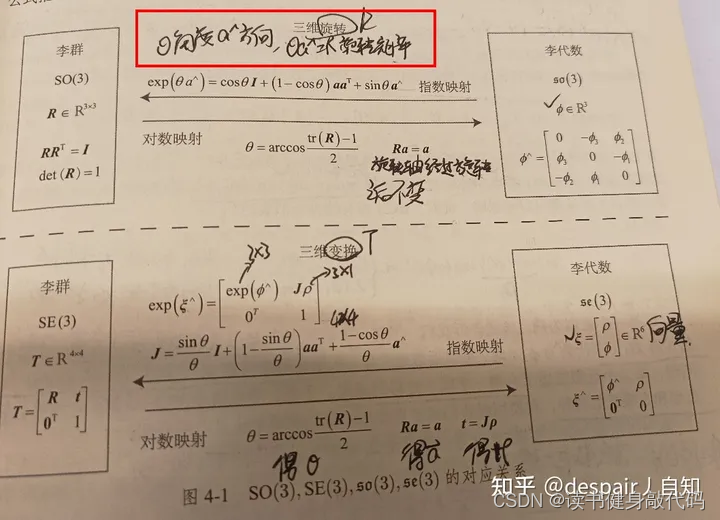
所以上述部分可以表示成 e x p [ ( ω b i t d + ω b i δ t d ) ∧ ] exp[(\omega_{b_i}t_d+\omega_{b_i}\delta t_d)^\wedge] exp[(ωbitd+ωbiδtd)∧],这只是便于理解,正常还是按照 ω t \omega t ωt表示,不加反对称符号。
所以,用到两个公式:
- 按照BCH公式的SO3版本:

- 还有 e x e^x ex的无穷级数展开(跟太了展开差个无穷小), e x = 1 + x + x 2 2 ! + x 3 3 ! + … e^x=1+x+\frac{x_2}{2!}+\frac{x_3}{3!}+\ldots ex=1+x+2!x2+3!x3+…,下面因为 ω b i δ t d \omega_{b_i}\delta t_d ωbiδtd较小,所以二阶以上直接忽略
所以
e x p ( ω b i t d + ω b i δ t d ) = e x p ( ω b i t d ) ∗ e x p { [ J r ( ω b i t d ) ω b i δ t d ] ∧ } = e x p ( ω b i t d ) ∗ { I + [ J r ( ω t d ) ω δ t d ] ∧ } \begin{align*}\ exp(\omega_{b_i}t_d+\omega_{b_i}\delta t_d) &=exp(\omega_{b_i}t_d) * exp\{[J_r(\omega_{b_i}t_d)\omega_{b_i}\delta t_d]^\wedge\}\\ &=exp(\omega_{b_i}t_d) * \{I + [J_r(\omega t_d)\omega \delta t_d]^\wedge \}\\ \end{align*} exp(ωbitd+ωbiδtd)=exp(ωbitd)∗exp{[Jr(ωbitd)ωbiδtd]∧}=exp(ωbitd)∗{I+[Jr(ωtd)ωδtd]∧}
将上式带入式(9)就得BCH近似后的结果,因为是求关于时间戳 t d t_d td的Jacobian,所以将与 δ t d \delta t_d δtd有关的都拎出来,剩下的直接扔掉,就得到完整的式(9)。
由于补偿camera pose的估计改变了姿态,所以Jacobian的求取有些复杂,QinTong(2018,在待读文献2中)有一个想法是直接补偿我们特征点的测量值,计算出补偿值,应用于真实观测值上得到一个虚拟的观测值。
1.2 思路2:补偿观测值坐标(特征匀速模型)
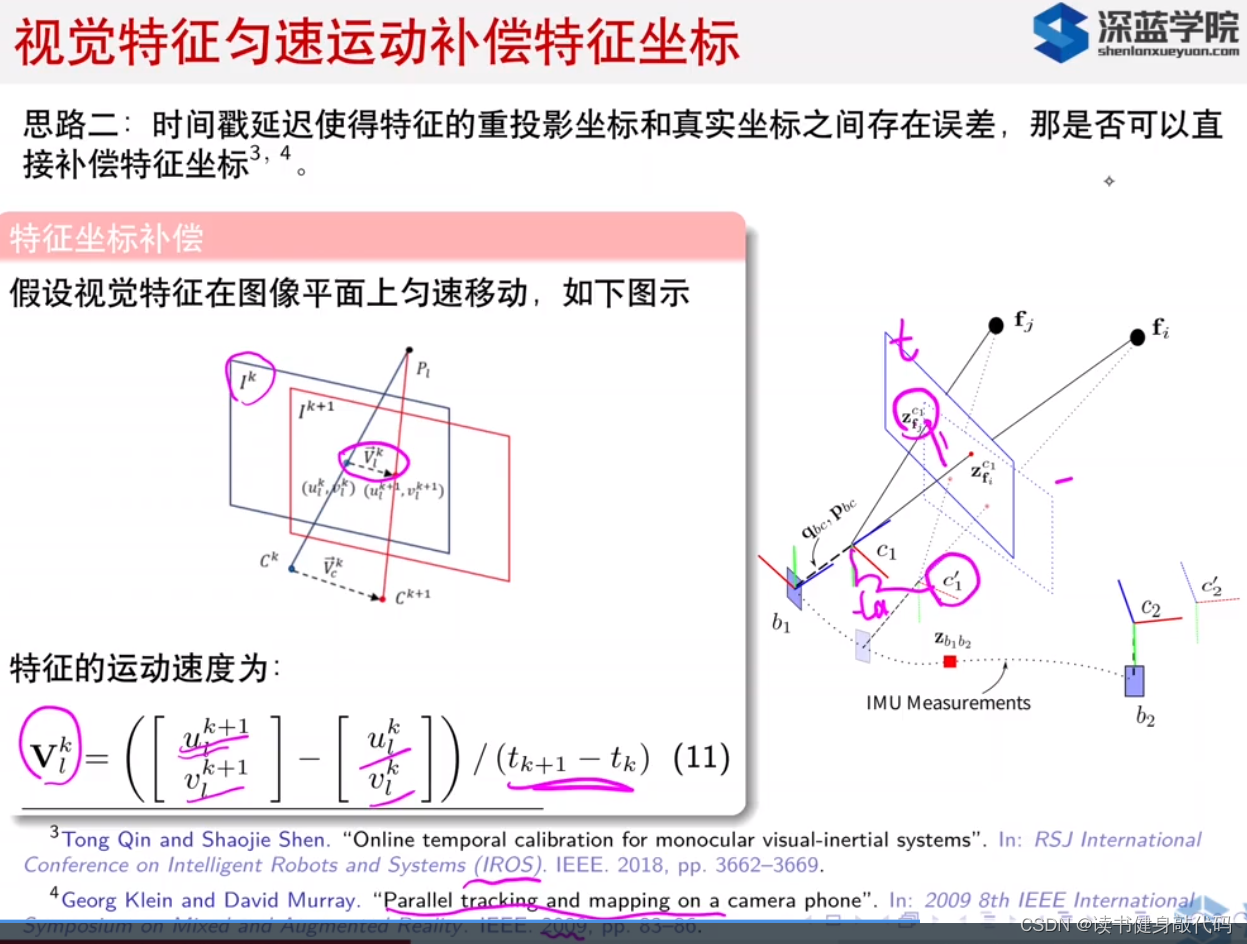
具体思路是:根据特征匹配可以知道特征点uv的变化量,假设特征点是匀速运动,可以算出特征点的速度,知道了时间戳偏移 t d t_d td之后即可求出补偿后的虚拟的观测值坐标。

补偿观测值坐标由于只改变了观测的坐标,所以求Jacobian较简单,看(13)中与 t d t_d td有关的只有 − u , − v -u,-v −u,−v,所以求导就是 − V -V −V
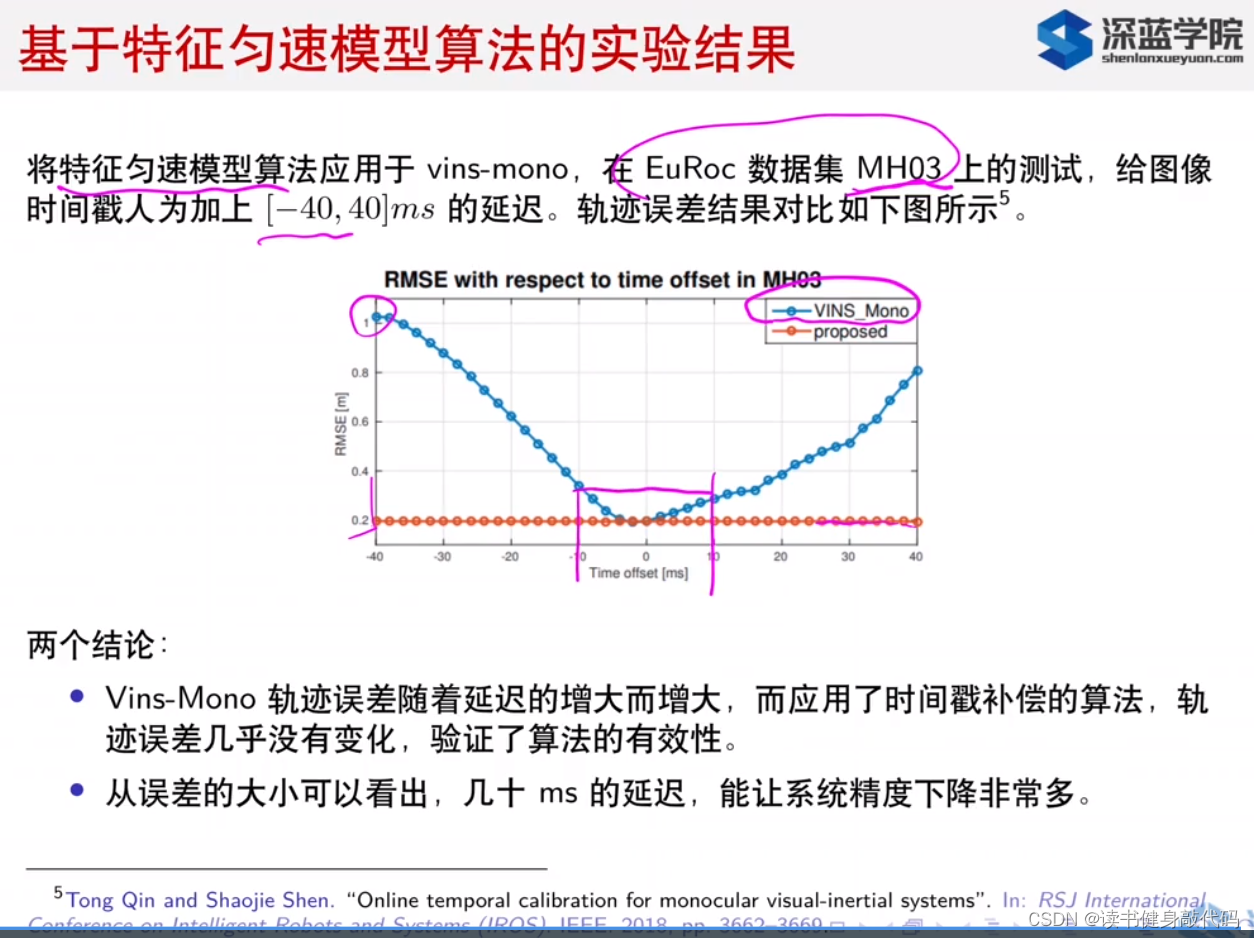
QinTong的paper论文实验结果和结论:
- 时间戳补偿算法有用;
- 时间戳延迟越大,系统精度下降越多。
1.3 两种方法对比
- 特征匀速模型的假设更强,是假设特征是匀速运动的,而实际上是非线性运动,并非匀速,且补偿方法也是线性的。
- 而轨迹匀速模型的假设更接近实际,假设两帧间camera是匀速运动,补偿方法也是非线性的,所以精度比前者高。
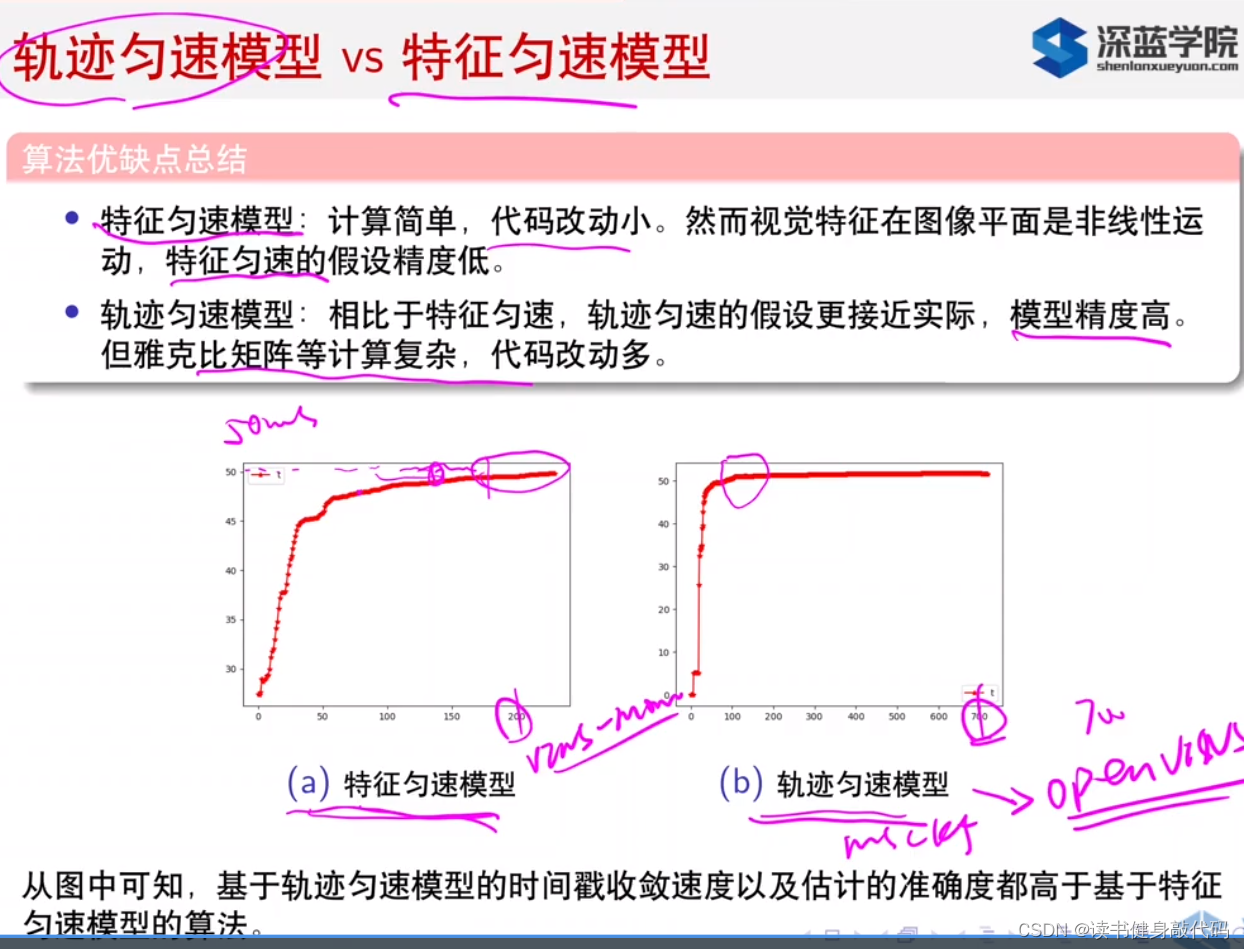
实际中对时间戳偏差估计的收敛速度,轨迹匀速法更快。
2. 疑惑
这个是先采集一段数据先标定出来IMU和Camera的时间戳,然后按照上面的任意一种方法补偿到系统中,还是说边估计边补偿?
看了些论文的标题,应该是先标定出来的,后面看了论文再来填这个坑。
3. 时间戳同步算法扩展

前面有系统初始化完成之后来估计 t d t_d td的,当系统初始化没有完成时 t d t_d td如何估计呢?
可以通过VO/SFM求出KF pose,利用 T b c T_{bc} Tbc外参转到body系下,求出i,j时刻的相对位姿,跟IMU预计分量对比构建误差,多时刻观测量可进行BA,优化出时间戳(也可优化出gyro bias,速度等,但是优化的量多了之后,优化精度可能会下降)

4. 总结
本章主要讨论了在VIO系统中对camera和IMU时间戳进行对齐的问题,着重讨论了将Camera对齐IMU的两种方法:轨迹匀速模型和特征匀速模型。并对其他的VI时间戳同步算法进行了扩展。
- 针对轨迹匀速模型和特征匀速模型:
- 前者假设两个KF间的camera之间是匀速运动,估计出时间戳延时 t d t_d td之后,将其补偿在估计的camera位姿上,该方法对VIO数据的pose进行了改动,对于系统Jacobian的改动较大,但假设相对后者较弱,精度比后者高。
- 后者假设两帧KF间的特征点是匀速运动,估计出 t d t_d td后,将其补偿在特征点的观测上,计算出补偿之后的观测,该方法对Jacobian改动较小,而且为线性改动,但缺点也较为明显,因为该方法假设较强(特征较难满足匀速运动),所以精度比前者低,时间戳收敛速度比前者慢,但代码改动小,计算速度简单。
- 另外对时间戳同步算法进行了扩展:
- 待读4改为对IMU进行时间戳补偿,精度更高;
- 待读5用camera的pose计算出traj,进而得出 ω , a \omega, a ω,a,与IMU的进行align得出 t d t_d td(这个不清楚,需要读原文)
- 待读6(提出Kalibr,行业标杆)使用标定板出一段camera pose,再使用B样条(B Spline)进行拟合,一阶,二阶导可以得出 ω , a \omega, a ω,a,和IMU数据进行align,优化出时间戳,不过使用的是autodiff 数值Jacobian。
- 待读7推导出6的解析李群Jacobian。
5. 作业

6. 待读文献
1. 北大的,提出轨迹匀速模型
Weibo Huang, Hong Liu, and Weiwei Wan. “Online initialization and extrinsic spatial-temporal calibration for monocular visual-inertial odometry”. In: arXiv preprint arXiv:2004.05534 (2020).
2. QinTong提出特征匀速模型
Tong Qin and Shaojie Shen. “Online temporal calibration for monocular visual-inertial systems”. In: RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE. 2018, pp. 3662–3669.
3. PTAM的特征匀速模型思路
Georg Klein and David Murray. “Parallel tracking and mapping on a camera phone”. In: 2009 8th IEEE International Symposium on Mixed and Augmented Reality. IEEE. 2009, pp. 83–86.
这篇是2009年的PTAM,里面的思想上面QinTong这篇一样。
4. 认为camera是准的,补偿IMU时间戳
Yonggen Ling et al. “Modeling varying camera-imu time offset in optimization-based visual-inertial odometry”. In: Proceedings of the European Conference on Computer Vision (ECCV). 2018, pp. 484–500.
这篇相对于第1节的算法,假设更弱,虽然轨迹匀速是假设camera见是匀速运动,但是如果是Slinding Window中的KF相隔时间久,可能存在较大时间差,匀速假设不易成立。
这篇改为补偿IMU,由于IMU频率高,数据之间的匀速假设更接近真实值,所以精度会更高,但是每次估计出新的时间戳都需要重新进行IMU预先积分,导致计算量增大。(没看过原文,IMU预积分不能找出来和时间戳的关系吗,这样就不用每次重新计算了)。
5. 用camera估出来的 ω , a \omega,a ω,a和IMU测量值进行align,得到时间戳偏移
Janne Mustaniemi et al. “Inertial-based scale estimation for structure from motion on mobile devices”. In: 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE. 2017, pp. 4394–4401.
6. ETH大组,Kalibr论文(行业标杆,必读)
Paul Furgale, Joern Rehder, and Roland Siegwart. “Unified temporal and spatial calibration for multi-sensor systems”. In: 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE. 2013, pp. 1280–1286.
Roland Siegwart好象是组的负责人。
使用标定板出一段camera pose,再使用B样条(B Spline)进行拟合,一阶,二阶导可以得出 ω , a \omega, a ω,a,和IMU数据进行align,优化出时间戳。但是解析解太复杂,这篇论文使用的autodiff数值Jacobian
7. 推导出解析Jacobian(DSO那个组,公式较多)
Christiane Sommer et al. “Efficient derivative computation for cumulative B-splines on Lie groups”. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020, pp. 11148–11156.
丹尼尔 crimse这个组






)


--lvgl - LVGL图像库)

)







