目录
遍历方式
示例
原理
前序遍历示例
二叉树的节点个数
原理
层序遍历
原理
这样做的目的是
判断完全二叉树
例题
编辑
思路
代码
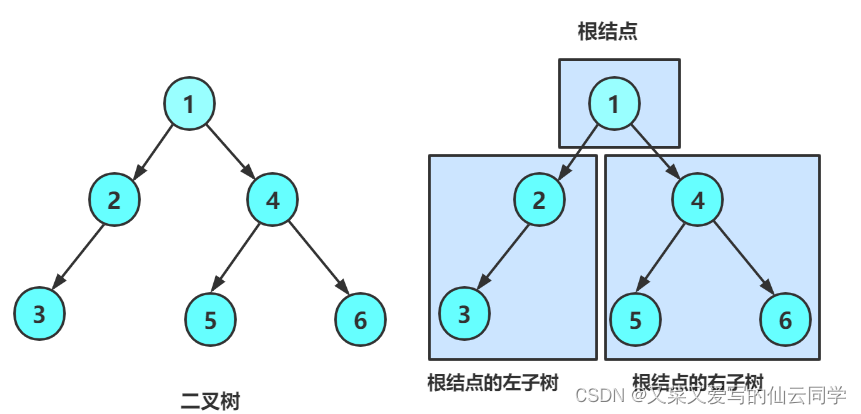
遍历方式
二叉树的遍历方式可分为:
前序遍历:先访问根,访问左子树,在访问右子树
中序遍历:先访问左子树,在访问根,最后访问右子树
后序遍历:先访问左子树,再访问右子树,最后访问根
示例
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi) {if (*pi >= n || a[*pi] == '#') {(*pi)++;return NULL;}BTNode* mn = (BTNode*)malloc(sizeof(BTNode));mn->_data = a[*pi];(*pi)++;mn->_left = BinaryTreeCreate(a, n, pi);mn->_right = BinaryTreeCreate(a, n, pi);;return mn;
}原理
首先判断当前节点是否为空,如果为空则return NULL
如果不为空
判断当前遍历方式
我们以前序遍历为例
先创建一个节点,将值赋给当前节点完成赋值给根的操作
然后在设置该节点的左子树与右子树
最后返回当前节点的指针实现递归操作
前序遍历示例
void BinaryTreePrevOrder(BTNode* root) {if (root == NULL)return;printf("%c", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}如果当前为空则返回,输出当前结点的值,访问左子树,访问右子树
二叉树的节点个数
int BinaryTreeSize(BTNode* root) {if (root == NULL)return 0;return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right)+1;
}原理
同样先设置终止条件:
当前节点为空返回0
如果当前节点不为空,则返回左子树的节点个数与右子树的节点个数加上当前节点本身的1即可实现递归操作
层序遍历
按从左往右,从上到下的顺序访问每个节点
void BinaryTreeLevelOrder(BTNode* root) {Queue mn;QueueInit(&mn);BTNode* now = root;QueuePush(&mn, now);while (!(QueueEmpty(&mn))) {printf("%c", QueueFront(&mn)->_data);now = QueueFront(&mn);if(now->_left)QueuePush(&mn, now->_left);if (now->_right)QueuePush(&mn, now->_right);QueuePop(&mn);}QueueDestroy(&mn);
}原理
先创建队列
将根节点放入队列
然后进入循环开始拆分
如果当前节点的左右子树不为空则将左右子树进入队列
每次循环都要先将队首元素输出同时删去队首元素
这样接下来的节点便会被一个一个访问到
这样做的目的是
节点被拆分的顺序是从上到下,先拆根,再拆根的左子树,再拆根的右子树
我们可以发现
这样便是从上到下,从左到右的顺序访问每一个节点
判断完全二叉树
int BinaryTreeComplete(BTNode* root) {Queue mn;QueueInit(&mn);BTNode* now = root;QueuePush(&mn, now);int tag = 0;while (!(QueueEmpty(&mn))) {printf("%c", QueueFront(&mn)->_data);now = QueueFront(&mn);if (tag && (now->_left || now->_right))return 0;if (now->_right && !now->_left)return 0;if (now->_left)QueuePush(&mn, now->_left);if (now->_right)QueuePush(&mn, now->_right);elsetag = 1;QueuePop(&mn);}QueueDestroy(&mn);return 1;
}与层序遍历是同样的操作,但是不同的是多了很多判断条件
但是最核心的内容始终是
如果没有左节点就存在右节点那么该树就不是完全二叉树
例题
链接:. - 力扣(LeetCode)

思路
我们可以先写一个函数用来判断两棵树是否相同,然后与原函数进行递归调用即可
代码
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if (q == NULL && p == NULL)return true;if (p == NULL || q == NULL)return false;if (q->val != p->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root==NULL)return false;if(isSameTree(root,subRoot))return true;return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}判断两棵树是否相同只需先判断当前节点是否相同,相同的话递归调用左右子树,只要左右子树也相同那么两棵树就相同
判断是否为子树只要采取一种遍历方式,只要当前节点不为空那么就判断当前节点开始的树是否与目标树相同,不同的话就拿左右子树进行判断,只要左右子树中存在与目标树相同的子树那么目标树即为原树的子树















可对接医保 采用云端SaaS模式部署)



)
