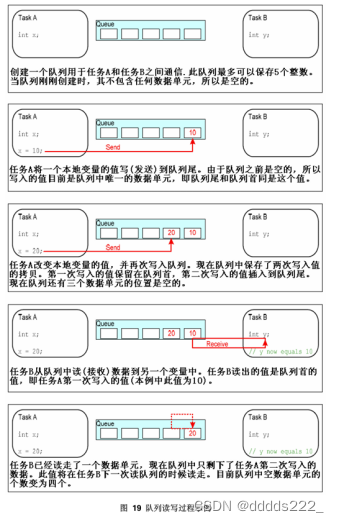
前提：

图：就是结点和边组成的数据结构

有向无环图：就是每一个边都有方向，且无法构成一个环，只有没有环的图才能进行拓扑排序，所以拓扑排序也能用来证明该图有没有环

在有向无环图中有两个概念：

入度：有多少条边指向该节点

出度：有多少条边从该节点出发

AOV网：对于DAG图的实际性应用，对其结点和边加了一些信息

例如：

BFS实现的拓扑排序的意义：

在AOV网中可以看出这些事情有的需要很多前提，而有的不需要前提就能直接做。

那么拓扑排序的意义就是，在AOV网中找到做事情的先后顺序

根据AOV网整理后得到的做事情的顺序为如图：

这个序列也就叫做拓扑序列

进行拓扑排序的步骤（结合题目）：

1.建图也就是建立AOV网或者说DAG图（如何建图在下文）

1.找到一个入度为0的点也就是不需要前提便可以直接做的事情，将其摘下来加入数组/或其他数据结构

2.然后删除该点其相连的边，也就是将其出度删除，那么其他点的入度便减少了

3.重复再找入度为零的点，直到图中没有点为止或者没有入度为0的点为止（图中有环）也就是可以判断图中是否有环

在bfs实现的拓扑排序中我们建图一般是通过邻接表来建立，结合该题目来看

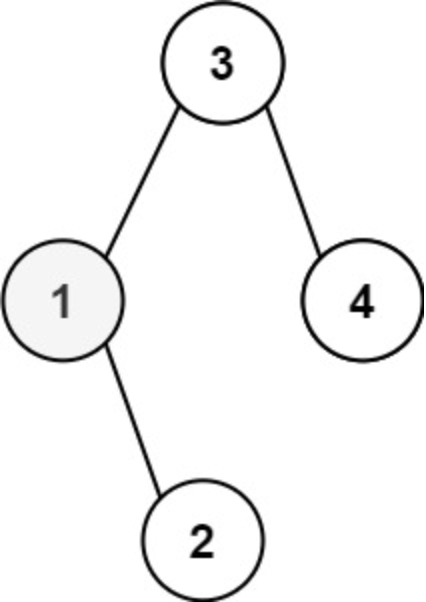
假设共有五个课程0，1，2，3，4，组成的DAG图为如图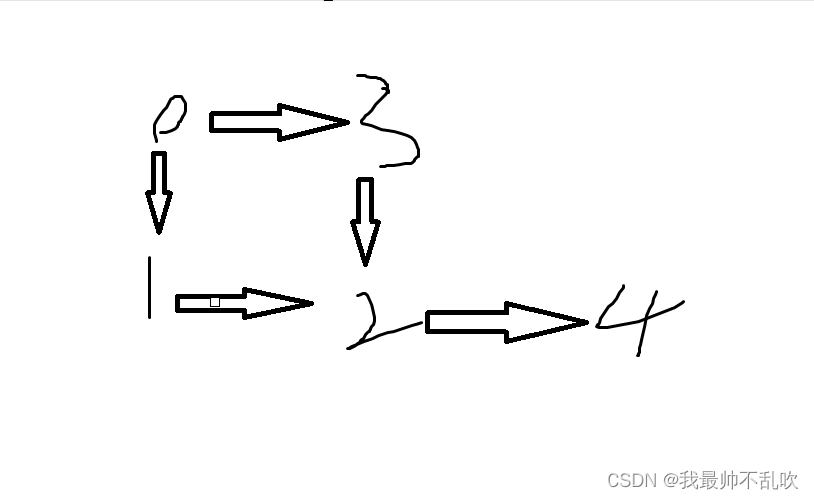

如上图为我们画出的邻接表，看第一个邻接表，0为头节点，箭头指向的是头节点的边指向的其他所有结点，因为形似链表且只隔边相接，所以叫做邻接表

所以邻接表就是DAG图中一个结点与其所有的出度指向的结点组成的一个结构

我们可以灵活使用c++提供的容器,我们可以使用二维数组，或者unordered_map来构建邻接表

vector<vector<int>>，可以用行的下标表示课程编号，用该行存储的数值表示指向的所有元素，但显然只能表示int类型的邻接表

unordered_map<Class=T,vector<T>>//前一个T，表示头节点的值，vector存储的是该头节点指向的所有元素，可以表示任何类型的邻接表

第二种方式更万能，更合适

2.再根据算法流程，灵活建图

再额外建立一个数组，用下标表示该结点的数字，存放的是该数字的入度。用来储存所有课程的入度

代码及其意义：

开始写代码：先把全部代码摆出来，接下来有具体模块代码的分析

class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {//readyunordered_map<int,vector<int>>AL;vector<int> intake(numCourses);//creat drawfor(auto i:prerequisites){int a=i[0],b=i[1];AL[b].push_back(a);intake[a]++;}//topo sortqueue<int>q;for(int i=0;i<intake.size();i++)//push in queue if node's num==0{if(intake[i]==0)q.push(i);}//bfswhile(q.size()){int top=q.front();q.pop();for(auto i :AL[top]){intake[i]--;if(intake[i]==0)q.push(i);}}//find thr retfor(auto i:intake)if(i!=0)return false;return true;}
};

如何联想到拓扑排序呢？该题中题目有提示性语句为在学习课程a前必须学习课程b，明显存在前提的条件，与AOV网各个结点需要入度为0才能进行相同，则可以联想到拓扑排序。

:构造一个邻接表。map<int,vector<int>>AL，前一个int表示课程的编号，后一个vector表示该课程出度指向的全部课程。然后又建立一个vectorintake，下标表示课程的编号，该位置的值表示该课程的入度。

 //readyunordered_map<int,vector<int>>AL;vector<int> intake(numCourses);

:确立了拓扑排序之后，则我们首先要开始建图。也就是初始化AL表和intake里所有课程的入度，那么遍历prerequistes的元素记为i。题目中表示i[1]=a为学习i[0]=b的前提，则我们将AL中a的邻接表中加入b，并在intake[b]++,因为检测到b的入度有一个a。

//creat drawfor(auto i:prerequisites){int a=i[0],b=i[1];AL[b].push_back(a);intake[a]++;}

:开始利用bfs进行拓扑排序。首先创立队列，然后将入度为0的课程加入到队列里面。对队列初始化。

  //topo sortqueue<int>q;for(int i=0;i<intake.size();i++)//push in queue if node's num==0{if(intake[i]==0)q.push(i);}

开始bfs搜索，取出队列中元素，遍历该元素为头节点的邻接表中全部指向的课程。因为已经取出了该头节点课程，所以头节点指向的课程的入度应该统统减一，然后别忘了判断如果入度减为0的话可以将其加入到队列中。

  //bfswhile(q.size()){int top=q.front();q.pop();for(auto i :AL[top]){intake[i]--;if(intake[i]==0)q.push(i);}}

广度优先搜索之后，就要返回结果了。我们可以通过遍历各个课程入度是否等于0来确定课程是否能够全部可以学（也就是判断DAG图中是否有环）如果全为0返回true，如果存在不为0的话返回false。

  //find thr retfor(auto i:intake)if(i!=0)return false;return true;