L2-001 紧急救援 最短路+路径打印

样例

输入1

4 5 0 3
20 30 40 10
0 1 1
1 3 2
0 3 3
0 2 2
2 3 2

输出1

2 60
0 1 3

分析

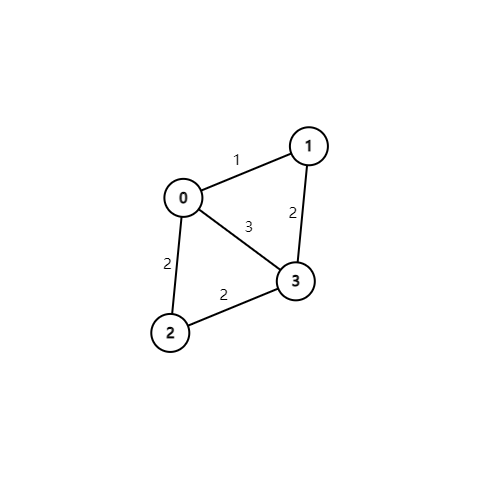
用一遍dijkstra算法。设立$num[i]$和$w[i]$表示从出发点到i结点拥有的路的条数，以及能够找到的救援队的数目

当判定$dis[u]+e[u][v]<dis[v]$的时候，不仅仅要更新$dis[v]$，还要更新$num[v]=num[u],w[v]=weight[v]+w[u]$；如果$dis[u]+e[u][v]==dis[v]$，还要更新$num[v]+=num[u]$，而且判断一下是否权重$w[v]$更小，如果更小了就更新$w[v]=weight[v]+w[u]$；

再设立一个$pre[i]$表示最短路径的前一个结点，在$dis[u]+e[u][v]<=dis[v]$的时候更新$pre[v]=u$，最后递归打印路径即可

代码

#include<stdio.h>
int n,m,s,d;
int num[550];//城市救援队数目 
int sf[550][550];//两座城市之间的距离 
int mins[550];//起始节点到其他节点的最短距离 
int flag[550];//标记是否作为过中间节点 
int max[100000];//从起始节点到其他节点召集救援队最大数目 
int cnt[100005];//存储从起始节点到其他节点的最短路径数目
int way[100005];//存储最短路径每个节点的前面一个节点 
const int INF=1e9+7;void dijistra();
void Print(int t);
int main()
{scanf("%d %d %d %d",&n,&m,&s,&d);for(int i=0;i<n;i++){scanf("%d",&num[i]);}for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(i==j){sf[i][j]=0;}else{sf[i][j]=INF;}}}int a,b,c;for(int i=0;i<m;i++){scanf("%d %d %d",&a,&b,&c);sf[a][b]=c;sf[b][a]=c;}dijistra();printf("%d %d\n",cnt[d],max[d]);Print(d);return 0;
} 
void dijistra()
{mins[s]=0;max[s]=num[s];cnt[s]=1;way[s]=s;for(int i=0;i<n;i++){mins[i]=sf[s][i];}while(1){int min_dist=INF;int mid=-1;for(int i=0;i<n;i++){if(flag[i]==0&&min_dist>mins[i]){min_dist=mins[i];mid=i;}}if(mid==-1){break;};flag[mid]=1;for(int i=0;i<n;i++){if(flag[i]==0){	if(mins[i]>mins[mid]+sf[mid][i]){mins[i]=mins[mid]+sf[mid][i];cnt[i]=cnt[mid];max[i]=max[mid]+num[i];way[i]=mid;}else{if(mins[i]==mins[mid]+sf[mid][i]){cnt[i]+=cnt[mid];if(max[i]<max[mid]+num[i]){max[i]=max[mid]+num[i];way[i]=mid;}}}}}}
}
void Print(int t)
{if(t==s){printf("%d",t);return;}Print(way[t]);printf(" %d",t);
}

L2-002 链表去重 模拟链表

样例

输入

00100 5
99999 -7 87654
23854 -15 00000
87654 15 -1
00000 -15 99999
00100 21 23854

输出

00100 21 23854
23854 -15 99999
99999 -7 -1
00000 -15 87654
87654 15 -1

分析：

数据量不大，可以直接用数组模拟链表，地址当做数组下标，考察基本的删除操作和尾插法。

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;struct node{ // 定义节点int id,val,next,absval; // 编号,键值,下一节点编号,绝对值
}LNode[N];
bool cmp(node a,node b){ // 按编号排序 以便二分查找return a.id<b.id;
}
pair<int,pair<int,int> > p;
vector<pair<int,pair<int,int> > > com,del;
int f[N];int main(){int ID,N,i; cin>>ID>>N; // 第一个结点的地址 和 结点总数for(i = 0 ; i < N ; i++){cin>>LNode[i].id>>LNode[i].val>>LNode[i].next; // 地址 键值 下一个结点LNode[i].absval=fabs(LNode[i].val); // 绝对值f[LNode[i].absval]=0; // 初始化每个绝对值的出现次数}sort(LNode,LNode+N,cmp); // 按编号排序while(ID!=-1){int l=0,r=N-1;	//二分查找下一节点 while(l<r){int mid=(l+r)/2;if(LNode[mid].id<ID) l=mid+1;else r=mid;}// p 的结构 <编号, <键值, 下一节点编号> >p.first=LNode[l].id;p.second.first=LNode[l].val;p.second.second=LNode[l].next;if(f[LNode[l].absval]==0){ // 当前绝对值还未出现过f[LNode[l].absval]=1; // 标记绝对值出现过com.push_back(p); // 当前节点加入保留队列}else del.push_back(p); // 当前绝对值出现过 ID=LNode[l].next; // 当前节点加入删除队列}for(i=0;i<com.size();i++){ // 输出保留节点队列if(i<com.size()-1)printf("%05d %d %05d\n",com[i].first,com[i].second.first,com[i+1].first);elseprintf("%05d %d -1\n",com[i].first,com[i].second.first);}for(i=0;i<del.size();i++){ // 输出删除节点队列if(i<del.size()-1)printf("%05d %d %05d\n",del[i].first,del[i].second.first,del[i+1].first);elseprintf("%5d %d -1\n",del[i].first,del[i].second.first);}return 0;
}

L2-003 月饼 贪心

样例：

输入

3 20
18 15 10
75 72 45

输出：

94.50

分析：

按照单价排序，优先选择单价最高的。库存量和总售价不一定为整数

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;struct node{ // 定义月饼结构体double num,price,dj; // 库存量,总售价,单价
}Mooncake[N];
bool cmp(node a,node b){ // 按月饼单价排序return a.dj>b.dj;
}
int main(){int n,m,k=0,i; cin>>n>>m; // 月饼的种类数n , 市场最大需求量m for(i=0;i<n;i++) cin>>Mooncake[i].num; // 每种月饼的库存量for(i=0;i<n;i++) cin>>Mooncake[i].price; // 每种月饼的总售价for(i=0;i<n;i++) Mooncake[i].dj=Mooncake[i].price/Mooncake[i].num; // 每种月饼的单价sort(Mooncake,Mooncake+n,cmp); // 按月饼单价排序double ans=0;for(int k = 0 ;  k < n ; k ++){ if(Mooncake[k].num <= m){ // 第 k 种月饼能全部卖出m-=Mooncake[k].num; ans+=Mooncake[k].price;}else{ // 第 k 种月饼不能全部卖出ans+=Mooncake[k].dj*m;break;}}printf("%.2lf\n",ans);return 0;
}

L2-004 这是二叉搜索树吗？ 数据结构

样例

输入样例 1：

7
8 6 5 7 10 8 11

输出样例 1：

YES
5 7 6 8 11 10 8

输入样例 2：

7
8 10 11 8 6 7 5

输出样例 2：

YES
11 8 10 7 5 6 8

输入样例 3：

7
8 6 8 5 10 9 11

输出样例 3：

NO

分析：

因为前序遍历是根左右，所以在插入某个孩子节点时，它的父节点肯定已经被插入了，又由于搜索树的限制关系（小的左边，大的右边），所以可以确定一棵唯一的二叉搜索树，然后对其进行两种不同的前序遍历，再分别与题目所给的序列比较即可。

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;struct node{ // 二叉树结点定义node *l,*r; // 左儿子结点, 右儿子结点int data; // 当前结点值
};
typedef node* Tree; // 定义二叉树
vector<int> s1,s2,s,ans; //s1为正常前序遍历，s2为左右儿子颠倒的前序遍历，s为输入序列
int n,cnt,x;
// 建立二叉树
Tree build(Tree root,int x){ if (root == NULL) { //到达最底部，创建新节点，并赋值root = new(node);root->l = root->r = NULL;root->data = x;}else if (x < root->data) // x小于当前节点，说明x在root的左半边，向左递归root->l = build(root->l, x);else // x不小于当前节点，说明x在root的右半边，向右递归root->r = build(root->r, x);return root;
}
//正常前序遍历
void pre1(Tree root) {if (root == NULL) return;s1.push_back(root->data);pre1(root->l);pre1(root->r);
}
//左右颠倒的前序
void pre2(Tree root) {if (root == NULL) return;s2.push_back(root->data);pre2(root->r);pre2(root->l);
}
//正常后序
void post1(Tree root) {if (root == NULL) return;post1(root->l);post1(root->r);ans.push_back(root->data);
}
//左右颠倒的后序
void post2(Tree root) {if (root == NULL) return;post2(root->r);post2(root->l);ans.push_back(root->data);
}
//比较两个序列是否完全相同
bool judge(vector<int> a) {for (int i = 0; i < a.size(); i++) if (a[i] != s[i]) return false;return true;
}
int main(){cin >> n; // N 个整数键值for (int i = 0; i < n; i++) cin >> x,s.push_back(x); // 加入队列 准备建树Tree root=NULL; // 创建树的根节点for (int i = 0; i < n; i++) root = build(root, s[i]); // 建树pre1(root); // 正常前序遍历pre2(root); // 左右颠倒的前序if (judge(s1)) {// 说明所给序列是二叉搜索树的前序遍历post1(root); // 正常后序puts("YES");for (int i = 0; i < n; i++) // 后序遍历的结果printf("%d%c", ans[i], i == n - 1 ? '\n' : ' ');}else if (judge(s2)) {//是镜像的前序遍历puts("YES");post2(root); // 左右颠倒的后序for (int i = 0; i < n; i++) // 后序遍历的结果printf("%d%c", ans[i], i == n - 1 ? '\n' : ' ');}else puts("NO"); // 不是二叉搜索树return 0;
}

L2-005 集合相似度 STL

样例

输入样例：

3
3 99 87 101
4 87 101 5 87
7 99 101 18 5 135 18 99
2
1 2
1 3

输出样例：

50.00%
33.33%

分析：

最多50个集合，预处理出全部的组合，C50 2=49∗25, 用set存放所有的集合，然后预处理的时候遍历两个set中较小的那个，在较大的中查找是否存在，将集合i和集合j共同拥有的数量存在both[i][j]中。Nc就是both[i][j]，Nt就是两个集合size加起来再减掉both[i][j]。时间复杂度：$25\ast 49\ast 10000\ast log(10000)=49000000$。

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;set<int> s[55]; // 用set存集合 避免出现重复数字int main(){int n; cin>>n; // 集合的个数int i,j,m,x;for(i = 0 ; i < n ; i ++){cin>>m; // 集合中元素的个数for(j = 0 ; j < m ; j ++){cin>>x; // 集合中的元素s[i].insert(x); // s[i] 存第i个集合}}int q;	cin>>q; // 查询次数while(q--){int x,y; cin>>x>>y; // 一对需要计算相似度的集合的编号x--,y--; // 存储编号从0开始, 但查询集合编号从1开始int num1=0, num2=s[x].size()+s[y].size();for(set<int>::iterator i=s[x].begin();i!=s[x].end();i++) // 遍历集合xif(s[y].count(*i)!=0) num1++;	//计算两个集合都有的不相等整数的个数 注意指针运算符printf("%.2lf%\n",num1*100.0/(num2-num1));}return 0;
}

L2-006 树的遍历 数据结构

样例

输入样例：

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例：

4 1 6 3 5 7 2

分析：

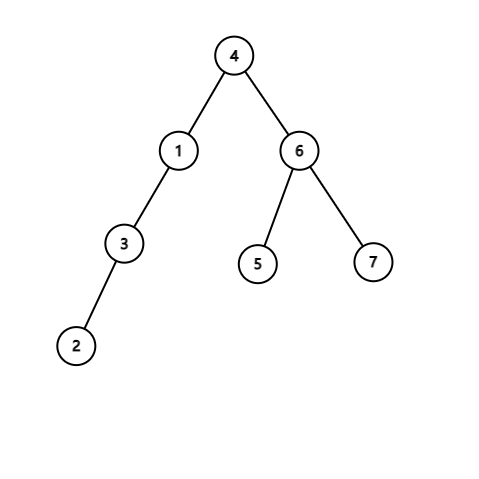
知道中序+后序或者前序，就能确定一棵唯一的二叉树。所以此题知道后序+中序，可以建立二叉树后层序遍历。由于后序是左右根，所以最后面的节点就是根，然后在中序中找到这个根的位置，左边就是左子树的范围，右边就是右子树的范围，递归处理即可。

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;
struct node{node *lson,*rson;int val;
};
typedef node* Tree;
vector<int> Mid_order, Post_order;
int n,x,i,now;	
Tree build(int l,int r){	//中序和后序建树 if(l>r) return NULL;Tree root = new(node);root -> val = Post_order[now];int mid = l;while(Post_order[now] != Mid_order[mid])mid++;now--;root -> rson = build(mid+1,r);root -> lson = build(l,mid-1);return root;
}void print(Tree root){	//层序遍历输出 queue<Tree> q;q.push(root);int tot = 0;while(!q.empty()){Tree t = q.front();if(t->lson != NULL)q.push(t->lson);if(t->rson != NULL)q.push(t->rson);printf("%d",t->val);q.pop();tot++;if(tot<n)cout<<' ';else cout<<endl;}
}int main(){cin>>n;for(i = 0 ; i < n ; i ++)cin>>x,Post_order.push_back(x);for(i = 0 ; i < n ; i ++)cin>>x,Mid_order.push_back(x);now = n - 1;print(build(0,n-1));return 0;
}

L2-007 家庭房产 并查集

样例

输入样例：

10
6666 5551 5552 1 7777 1 100
1234 5678 9012 1 0002 2 300
8888 -1 -1 0 1 1000
2468 0001 0004 1 2222 1 500
7777 6666 -1 0 2 300
3721 -1 -1 1 2333 2 150
9012 -1 -1 3 1236 1235 1234 1 100
1235 5678 9012 0 1 50
2222 1236 2468 2 6661 6662 1 300
2333 -1 3721 3 6661 6662 6663 1 100

输出样例：

3
8888 1 1.000 1000.000
0001 15 0.600 100.000
5551 4 0.750 100.000

分析：

用并查集维护集合关系，由于要输出最小编号，合并时将较大的合并给较小的点，由于编号一共最多到9999，记录每个编号是否出现过，然后遍历一遍，将每个编号所拥有的房产等信息贡献给父节点。之后按照题目要求排序输出即可。
坑：编号可能会有0000

代码：

#include<bits/stdc++.h>
using namespace std;
#define PII pair<int,int>
const int N = 1e4+10;struct node{ // 父节点int id, kou, fang, mian; // 编号，人口，房产数量，房产面积double x1, x2; // 人均房产套数，人均房产面积const bool operator < (const node &t) const { if(t.x2 == x2) return id < t.id; // 若有并列，则按成员编号的升序return x2 > t.x2; // 先按人均面积降序}
}p[N];int n;
int fa[N],vis[N],num[N],s[N];void init(int n) { for ( int i = 0 ; i < n ; i++ ) fa[i] = i; }	//初始化 
int find(int x) { return fa[x] == x ? x : fa[x] = find( fa[x] ); }	//查找 路径压缩 
void merge(int a,int b){ a = find(a), b = find(b); fa[max(a,b)] = min(a,b);}	//家族最小值作为祖先 int main(){cin>>n; // n个人的房产init(N); //初始化 while(n--){int id,fid,mid,k,ID; cin>>id>>fid>>mid>>k; // 编号，父编号，母编号，孩子数量vis[id] = 1;// 活人编号大于0if(fid >= 0) merge(id,fid), vis[fid]=1;if(mid >= 0) merge(id,mid), vis[mid]=1;while(k--){int cid; cin>>cid; // 孩子编号vis[cid] = 1;merge(id,cid);}cin>>num[id]>>s[id]; // 房产套数 总面积}for(int i = 0 ; i < N ; i ++) { // 遍历所有编号if(vis[i]) { // 寻找活着的人int x = find(i); // 查找当前编号的家庭祖先p[x].kou ++; // 家庭人口 p[x].fang += num[i]; // 家庭房产数量p[x].mian += s[i]; // // 家庭房产面积}}vector<node> ans;for(int i = 0; i < N; i++) { // 遍历所有编号 if(vis[i] && find(i) == i) { // 寻找家庭p[i].id = i; // 家庭编号p[i].x1 = p[i].fang * 1.0 / p[i].kou; // 家庭人均房产套数p[i].x2 = p[i].mian * 1.0 / p[i].kou; // 家庭人均房产面积ans.push_back(p[i]);}}sort(ans.begin(), ans.end()); // 按人均面积降序输出，若有并列，则按成员编号的升序输出cout << ans.size() << endl;for(int i = 0; i < ans.size(); i++) printf("%04d %d %.3lf %.3lf\n",ans[i].id,ans[i].kou,ans[i].x1,ans[i].x2); return 0;
}

L2-008 最长对称子串 字符串

样例

输入样例：

Is PAT&TAP symmetric?

输出样例：

11

分析：

回文串问题，manacher模板题

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;string s,s_new;
int p[N*2];void init(){	//初始化s_new+='$';s_new+='#';for(int i=0;i<s.size();i++){s_new+=s[i];s_new+='#';}s_new+='\0';
}
void Manacher(){init();int mx=0,di,ans=0;for(int i=0;i<s_new.size();i++){p[i] = mx > i ? min(p[2 * di - i], mx - i) : 1;while(s_new[i-p[i]] == s_new[i+p[i]]) p[i]++;if(i+p[i] > mx){mx = i+p[i];di = i;ans = max(ans,p[i]);}}printf("%d\n",ans-1);
}
int main(){getline(cin,s);Manacher();return 0;
}

L2-009 抢红包 排序

样例

输入样例：

10
3 2 22 10 58 8 125
5 1 345 3 211 5 233 7 13 8 101
1 7 8800
2 1 1000 2 1000
2 4 250 10 320
6 5 11 9 22 8 33 7 44 10 55 4 2
1 3 8800
2 1 23 2 123
1 8 250
4 2 121 4 516 7 112 9 10

输出样例：

1 11.63
2 3.63
8 3.63
3 2.11
7 1.69
6 -1.67
9 -2.18
10 -3.26
5 -3.26
4 -12.32

分析：

就是细节题，题目让你干什么就干什么。结构体中自定义排序规则

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;struct node{ //定义每个人的结构体int id,money,num; // 编号,抢到的红包金额,抢到的红包数量
}peo[N];
bool cmp(node a,node b){if(a.money==b.money) return a.num>b.num; // 收入金额有并列，则按抢到红包的个数递减return a.money>b.money; // 按照收入金额从高到低的递减
}
int main(){int n;	cin>>n; // 参与发红包和抢红包的总人数for(int i = 1 ; i <= n ; i ++) peo[i].id = i;for(int i = 1 ; i <= n ; i ++){int k,sum=0;	cin>>k; // 发出去的红包个数for(int j = 0 ; j < k ; j++){int x,m;	cin>>x>>m; // 抢到红包的人的编号,其抢到的红包金额peo[x].money += m;sum += m;peo[x].num ++;}peo[i].money -= sum;}sort(peo+1,peo+1+n,cmp);for(int i = 1 ; i <= n ; i ++)printf("%d %.2lf\n", peo[i].id, peo[i].money*1.0/100);return 0;
}

L2-010 排座位 dfs

样例

输入样例：

7 8 4
5 6 1
2 7 -1
1 3 1
3 4 1
6 7 -1
1 2 1
1 4 1
2 3 -1
3 4
5 7
2 3
7 2

输出样例：

No problem
OK
OK but...
No way

分析：

N≤100，说明可以直接建图后进行dfs遍历，只遍历边权为1的点，如果可以从a走到b，说明有共同朋友，再判断mp[a][b]是否为-1即可。其他情况类似。

代码：

#include <bits/stdc++.h>
#define LL long long
using namespace std;
int n, m, k, a, b, c;
int mp[111][111],vis[111];bool dfs(int now,int end) {if(now==end) return true;for(int i=1;i<=n;i++){if(mp[now][i]==1&&vis[i]==0){vis[now]=1;if(dfs(i,end)) return true;vis[now]=0;}}return false;
}int main() {cin >> n >> m >> k; // 宾客总人数n, 关系数m, 查询的条数k, for (int i = 0; i < m; i++) { // 输入 并 建双向图cin >> a >> b >> c; // 宾客1 宾客2 关系mp[a][b] =  mp[b][a] = c;}while (k--) {cin >> a >> b; // 一对需要查询的宾客编号for(int i=1;i<=n;i++) vis[i]=0;vis[a]=1;bool flag=dfs(a,b);if(flag && mp[a][b]!=-1) cout<<"No problem"<<endl; // 两位宾客之间是朋友，且没有敌对关系if(flag && mp[a][b]==-1) cout<<"OK but..."<<endl; // 两位宾客之间并不是朋友，但也不敌对if(!flag && mp[a][b]!=-1) cout<<"OK"<<endl; // 两位宾客之间有敌对，然而也有共同的朋友if(!flag && mp[a][b]==-1) cout<<"No way"<<endl; // 两位宾客之间只有敌对关系}return 0;
}

L2-011 玩转二叉树 数据结构

样例

输入样例：

7
1 2 3 4 5 6 7
4 1 3 2 6 5 7

输出样例：

4 6 1 7 5 3 2

分析：

就是两种遍历方式求另外一种，PTA好喜欢这种题，镜面翻转其实就是在求层序的时候反着放入队列就行。

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;struct node{node *l,*r;int data;
}; 
typedef node* Tree;
int i,n,x,now=0;
vector<int> pre_order,mid_order;
Tree build(int l,int r){if(l>r) return NULL;Tree root=new(node);root->data=pre_order[now];int mid=l;while(pre_order[now] != mid_order[mid]) mid++;now++;root->l = build(l, mid - 1);root->r = build(mid + 1, r);return root;
}
void printf(Tree root){queue<Tree> q;q.push(root);int tot=0;while(q.size()){Tree t=q.front();tot++;printf("%d%c",t->data,tot==n ? '\n' : ' ');q.pop();if(t->r!=NULL) q.push(t->r);if(t->l!=NULL) q.push(t->l); }
}
int main(){cin>>n; // 二叉树中结点的个数for(i = 1 ; i <= n ; i++) cin>>x,mid_order.push_back(x); // 中序遍历序列for(i = 1 ; i <= n ; i++) cin>>x,pre_order.push_back(x); // 前序遍历序列printf(build(0,n-1)); // 建树 并 输出层序遍历的序列return 0;
}

L2-012 关于堆的判断

样例

输入样例：

5 4
46 23 26 24 10
24 is the root
26 and 23 are siblings
46 is the parent of 23
23 is a child of 10

输出样例：

F
T
F
T

代码

#include <bits/stdc++.h> 
#include <unordered_map> 
using namespace std; 
#define LL long long 
const int maxn = 1e3+10; 
const int inf = 0x3f3f3f3f; 
const double PI = acos(-1.0); 
typedef pair<int,int> PII; int heap[maxn], n, cnt, m; // 定义小顶堆数组、元素个数、计数器、判断的命题数
unordered_map<int,int> f; // 定义哈希映射，用于存储元素值及其对应的下标void up(int x) { // 实现堆的向上调整操作if(x >> 1 >= 1 && heap[x] < heap[x>>1]) { // 如果当前节点不是根节点且小于其父节点swap(heap[x],heap[x>>1]); // 交换当前节点和其父节点的值up(x>>1); // 继续向上调整}
}int main() { // 主函数cin >> n >> m; // 输入元素个数和命题数for(int i = 0; i < n; i++) { // 循环读入要被插入小顶堆的整数cin >> heap[++cnt]; // 读入一个元素并更新计数器up(cnt); // 对新插入的元素进行向上调整操作}for(int i = 1; i <= n; i++) f[heap[i]] = i; // 构建元素值和下标的映射关系while(m--) { // 循环处理每个命题int x, y; // 定义变量用于存储命题中的数字string s; // 定义字符串变量用于存储命题中的字符串cin >> x >>s; // 读入数字和字符串x = f[x]; // 将数字转换为在堆中的下标if(s == "and") { // 如果命题为 "and"cin >> y >> s >>s; // 读入数字和字符串y = f[y]; // 将数字转换为在堆中的下标if((x >> 1) == (y >> 1)) puts("T"); // 判断两个数字的父节点是否相同并输出结果else puts("F"); // 若父节点不同则输出 "F"} else { // 若命题不为 "and"cin >> s >> s; // 读入字符串if(s == "root") { // 如果命题为 "root"if(x == 1) puts("T"); // 判断当前节点是否为根节点并输出结果else puts("F"); // 若不为根节点则输出 "F"} else if(s == "parent") { // 若命题为 "parent"cin >> s >> y; // 读入字符串和数字y = f[y]; // 将数字转换为在堆中的下标if((y >> 1) == x) puts("T"); // 判断当前节点是否为指定节点的父节点并输出结果else puts("F"); // 若不是指定节点的父节点则输出 "F"} else if(s == "child") { // 若命题为 "child"cin >> s >> y; // 读入字符串和数字y = f[y]; // 将数字转换为在堆中的下标if((x >> 1) == y) puts("T"); // 判断当前节点是否为指定节点的孩子节点并输出结果else puts("F"); // 若不是指定节点的孩子节点则输出 "F"}}}return 0; // 程序正常结束
}
/*
input
5 4
46 23 26 24 10
24 is the root
26 and 23 are siblings
46 is the parent of 23
23 is a child of 10
output
F
T
F
T
*/

L2-013 红色警报 并查集

样例

输入样例：

5 4
0 1
1 3
3 0
0 4
5
1 2 0 4 3

输出样例：

City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.

分析：

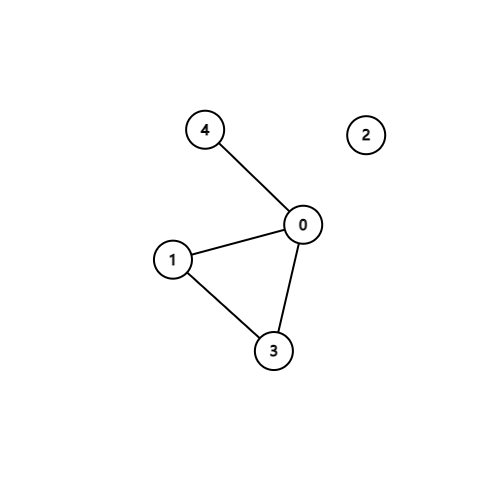
每次删去一个点，可以用一个数组记录标记被删去的点，每删去一个点，对所有不包含被删去点的边求一次并查集，检查有几个集合，如果比之前多则说明有国家被分裂了，注意已经被消灭的城市不会算入一个集合。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N=505;int n,m,k,x,y;
int fa[N],vis[N];
vector<PII> v;void init(int n) { for ( int i = 0 ; i < n ; i++ ) fa[i] = i; }	//初始化 
int find(int x) { return fa[x] == x ? x : fa[x] = find( fa[x] ); }	//查找 路径压缩 
void merge(int a, int b) { a = find(a), b = find(b), fa[b] = a; }	//合并 int fun(int x){init(n);vis[x]=0;	//x城市被攻占for(int i=0;i<v.size();i++)if(vis[v[i].first]+vis[v[i].second]==2)merge(v[i].first,v[i].second);int res=0;for(int i=0;i<n;i++)if(vis[i]==1&&fa[i]==i)res++;return res;
}int main(){cin>>n>>m;//城市个数n, 通路条数mfor(int i = 1 ; i <= m ; i++){cin>>x>>y; // 连接的两个城市的编号v.push_back({x,y}); // 建立单向边}cin>>k; // K个被攻占的城市的编号for(int i = 0 ; i < n ; i++) vis[i]=1;int num=fun(n);while(k--){cin>>x; // 攻占的城市的编号int t=fun(x);if(t>num) printf("Red Alert: City %d is lost!\n",x); // 改变整个国家的连通性else printf("City %d is lost.\n",x);if(t==0) printf("Game Over.\n"); // 失去了最后一个城市num=t;}
}

L2-014 列车调度 STL

样例

输入样例：

9
8 4 2 5 3 9 1 6 7

输出样例：

4

分析：

可以这样调度：先查看当前所有轨道的最左边火车编号是否小于当前编号，插入到最小的比当前火车编号大的火车后，如果不存在则开辟新轨道。可知，轨道的最左端火车编号一定是随轨道下标而递增的，可以用二分查找快速找到那条轨道。当然，可以用set更为方便。

代码：

#include<iostream>
#include<set>
using namespace std;
int main()
{int n; scanf("%d",&n); // N条平行的轨道set<int>sc;for(int i=0;i<n;i++){int k; scanf("%d",&k);set<int>::iterator it=sc.lower_bound(k);if(it!=sc.end()){sc.erase(it);sc.insert(k);}elsesc.insert(k);}cout<<sc.size();
}

L2-015 互评成绩 排序

样例

输入样例：

6 5 3
88 90 85 99 60
67 60 80 76 70
90 93 96 99 99
78 65 77 70 72
88 88 88 88 88
55 55 55 55 55

输出样例：

87.667 88.000 96.000

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;int n,k,m,i,j,x;
vector<int> vi;
vector<double> vd;int main(){cin>>n>>k>>m; // 学生总数n, 每份作业的评审数k, 需要输出的学生数mfor(i = 1 ; i <= n ; i++){vi.clear();for(j=0;j<k;j++) cin>>x,vi.push_back(x); // 评审成绩sort(vi.begin(),vi.end());vi.erase(vi.begin()); // 去掉一个最高分vi.erase(vi.end()-1); // 去掉一个最低分int sum=0;for(j=0;j<vi.size();j++) sum+=vi[j]; // 剩下的分数求和vd.push_back(sum*1.0/(k-2)); // 取平均}sort(vd.begin(),vd.end()); // 按非递减顺序输出最高的M个成绩for(i=vd.size()-m;i<vd.size();i++)printf("%.3lf%c",vd[i],i==vd.size()-1?'\n':' ');return 0;
}

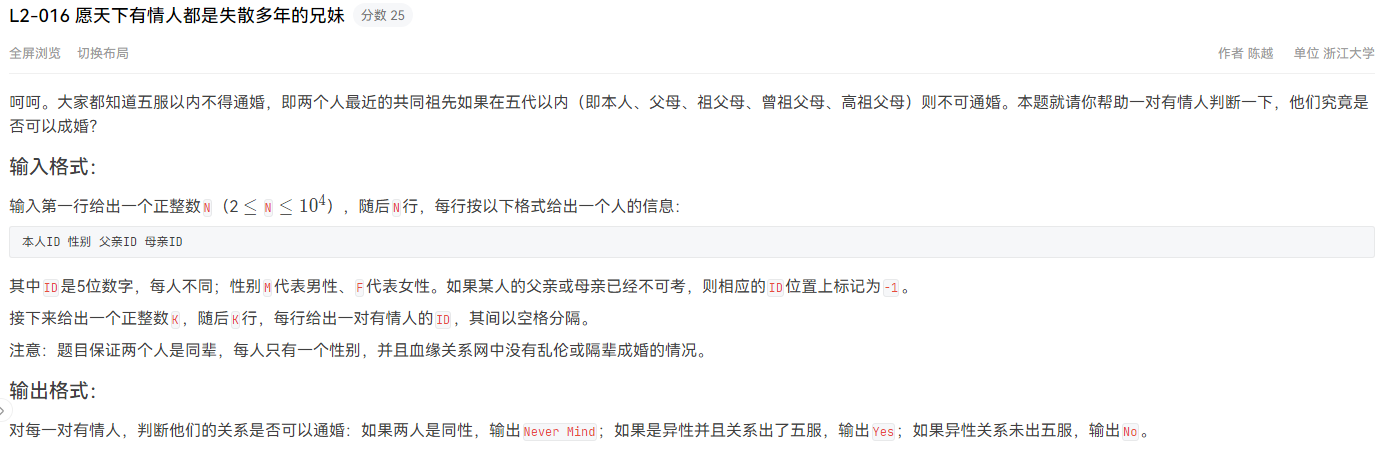
L2-016 愿天下有情人都是失散多年的兄妹 dfs

样例

输入样例：

24
00001 M 01111 -1
00002 F 02222 03333
00003 M 02222 03333
00004 F 04444 03333
00005 M 04444 05555
00006 F 04444 05555
00007 F 06666 07777
00008 M 06666 07777
00009 M 00001 00002
00010 M 00003 00006
00011 F 00005 00007
00012 F 00008 08888
00013 F 00009 00011
00014 M 00010 09999
00015 M 00010 09999
00016 M 10000 00012
00017 F -1 00012
00018 F 11000 00013
00019 F 11100 00018
00020 F 00015 11110
00021 M 11100 00020
00022 M 00016 -1
00023 M 10012 00017
00024 M 00022 10013
9
00021 00024
00019 00024
00011 00012
00022 00018
00001 00004
00013 00016
00017 00015
00019 00021
00010 00011

输出样例：

Never Mind
Yes
Never Mind
No
Yes
No
Yes
No
No

分析

先跑一遍dfs标记第一个人的所有五代内的长辈，然后再dfs一遍第二个人的所有五代内的长辈，检查是否有重复。有个坑点就是：父母的性别都是已知的，但是可能不会告诉你父母的祖辈情况，所以要同时记录父母的性别，否则父母性别默认初始值都是相同的了。还有个我自己的问题，直接在结构体内赋值的方式进行初始化，这样是不可行的，正确方法是要么循环遍历初始化，要么写一个构造函数。

代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5+10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int,int> PII;
struct node
{int fa, ma, sex , flag;node() {flag = 0;fa = ma = -1;}
}peo[maxn];
int f;
int vis[maxn];
void dfs(int x, int ceng) {if(x == -1 || ceng > 5) return;vis[x] = 1;if (peo[x].flag == 0) return;dfs(peo[x].ma, ceng + 1);dfs(peo[x].fa,ceng+1);
}
void dfs2(int x, int ceng) {if(x == -1 || ceng > 5 || f == 1) return;if(vis[x] == 1) {f = 1;return;}if (peo[x].flag == 0) return;dfs2(peo[x].ma,ceng+1);dfs2(peo[x].fa,ceng+1);
}int main(int argc, char const *argv[]) {int n;cin >> n;for(int i = 1; i <= n; i++) {string s;int id;cin >> id >> s;cin >> peo[id].fa >> peo[id].ma;peo[id].flag = 1;if(s[0] == 'M') peo[id].sex = 1;else peo[id].sex = 0;if(peo[id].fa != -1)peo[peo[id].fa].sex = 1;if(peo[id].ma != -1)peo[peo[id].ma].sex = 0;}int k;cin >> k;while(k--) {memset(vis, 0 ,sizeof vis);int x, y;cin >> x >> y;if(peo[x].sex == peo[y].sex) puts("Never Mind");else {f = 0;dfs(x,1);dfs2(y,1);if(f==0) puts("Yes");else puts("No");}}return 0;
}

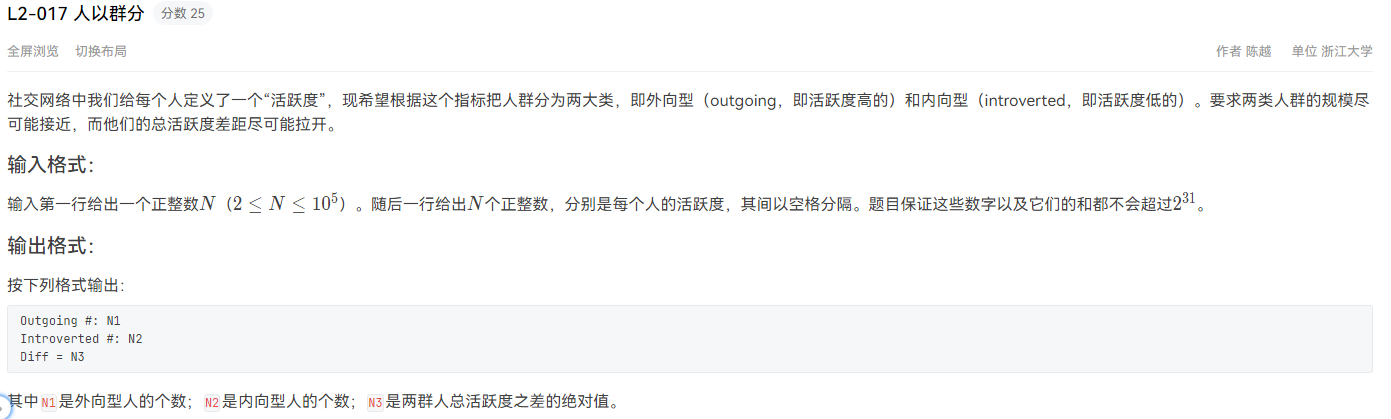
L2-017 人以群分 水题

样例

输入样例1：

10
23 8 10 99 46 2333 46 1 666 555

输出样例1：

Outgoing #: 5
Introverted #: 5
Diff = 3611

输入样例2：

13
110 79 218 69 3721 100 29 135 2 6 13 5188 85

输出样例2：

Outgoing #: 7
Introverted #: 6
Diff = 9359

分析：

要先保证人数平均再保证差值尽量大，那么就排序后平均分成两份的差值会最大，如果人数为奇数，中间值分给外向的人群可以使得差值最大。

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;vector<int> v;
int n,x,i,sum1,sum2;int main(){cin>>n;sum1=sum2=0;while(n--){cin>>x;v.push_back(x);}sort(v.begin(),v.end());for(i=0;i<v.size()/2;i++) sum1+=v[i];for(i=v.size()/2;i<v.size();i++) sum2+=v[i];printf("Outgoing #: %d\n",v.size()-v.size()/2);printf("Introverted #: %d\n",v.size()/2);printf("Diff = %d\n",sum2-sum1);return 0;
}

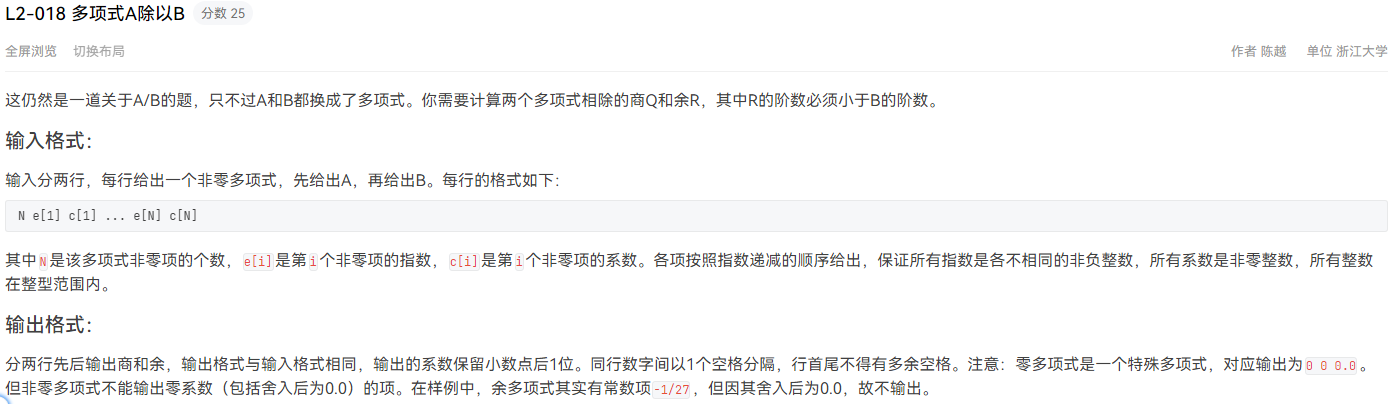
L2-018 多项式A除以B 模拟

样例

输入样例：

4 4 1 2 -3 1 -1 0 -1
3 2 3 1 -2 0 1

输出样例：

3 2 0.3 1 0.2 0 -1.0
1 1 -3.1

分析：

模拟手算多项式除法即可，注意细节

代码：

#include<bits/stdc++.h>
using namespace std;const int maxn=3e3+10;
double c1[maxn],c2[maxn],c3[maxn];int nonNegativeNum(double c[],int st)//统计非负项个数 
{int cnt=0;for(int i=st;i>=0;--i)if(abs(c[i])+0.05>=0.1)cnt++;return cnt;
}
void printPoly(double c[],int st)
{printf("%d",nonNegativeNum(c,st));if(nonNegativeNum(c,st)==0)printf(" 0 0.0");for(int i=st;i>=0;--i)if(abs(c[i])+0.05>=0.1)printf(" %d %.1lf",i,c[i]);
}
int main() 
{int max1=-1,max2=-1;int m;scanf("%d",&m);for(int i=0;i<m;++i){int t;scanf("%d",&t);max1=max(max1,t);scanf("%lf",&c1[t]);}int n;scanf("%d",&n);for(int i=0;i<n;++i){int t;scanf("%d",&t);max2=max(max2,t);scanf("%lf",&c2[t]);}int t1=max1,t2=max2;while(t1>=t2){double x=c1[t1]/c2[t2];//最高次幂的商的系数 c3[t1-t2]=x;for(int i=t1,j=t2;j>=0;--j,--i)c1[i]-=c2[j]*x; while(abs(c1[t1])<1e-6)t1--;//如果该项是0，那么最高次幂降1； }printPoly(c3,max1-max2);puts("");printPoly(c1,t1);return 0;
}

L2-019 悄悄关注 STL

样例

输入样例1：

10 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao
8
Magi 50
Pota 30
LLao 3
Ammy 48
Dave 15
GAO3 31
Zoro 1
Cath 60

输出样例1：

Ammy
Cath
Pota

输入样例2：

11 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao Pota
7
Magi 50
Pota 30
LLao 48
Ammy 3
Dave 15
GAO3 31
Zoro 29

输出样例2：

Bing Mei You

分析：

map记录一下哪些名字出现过，再用一个map记录点赞情况并求出平均值，遍历记录点赞记录的map，将满足条件的名字放入vector，排序输出。

代码：

#include<bits/stdc++.h>
using namespace std;const int N=1e5+5;
typedef long long ll;
typedef pair<string,int> Psi;Psi p;
set<string> s;
vector<Psi> v1;
vector<string> v2;
string str;
int n,i,m,num,sum;int main(){cin>>n;getchar();for(i=0;i<n;i++){cin>>str;s.insert(str);}cin>>m;getchar();sum=0;for(i=0;i<m;i++){cin>>str>>num;sum+=num;p.first=str,p.second=num;v1.push_back(p);}sum/=m;for(i=0;i<v1.size();i++)if(s.count(v1[i].first)==0&&v1[i].second>sum)v2.push_back(v1[i].first);sort(v2.begin(),v2.end());if(v2.size()){for(i=0;i<v2.size();i++)cout<<v2[i]<<endl;}else cout<<"Bing Mei You"<<endl;return 0;
}

L2-020 功夫传人 dfs

样例

输入样例：

10 18.0 1.00
3 2 3 5
1 9
1 4
1 7
0 7
2 6 1
1 8
0 9
0 4
0 3

输出样例：

404

分析：

由于每个徒弟严格只会跟一个高一辈的师傅，直接保存每个人的徒弟，然后dfs一遍就行，标记一下超级徒弟dfs的时候判断一下就行，超级徒弟就是叶子节点。

代码：

#include<bits/stdc++.h>
using namespace std;
#define PII pair<int,int>const int INF = 0x3f3f3f3f;
const int N = 1e5+10;int n;
int vis[N];
double z,r,sum; 
vector<int> v[N];void dfs(int x,double power){if(vis[x]){sum+=power*v[x][0];return ;}for(int i=0;i<v[x].size();i++)dfs(v[x][i],power*r);
}int main(){cin>>n>>z>>r;r=(100.0-r)/100.0;for(int i=0;i<n;i++){int k,x; cin>>k;if(k==0) {cin>>x;vis[i]=1;v[i].push_back(x);}while(k--){cin>>x;v[i].push_back(x);}}dfs(0,z);cout<<(int)sum<<endl;return 0;
}

L2-021 点赞狂魔 排序

样例

输入样例：

5
bob 11 101 102 103 104 105 106 107 108 108 107 107
peter 8 1 2 3 4 3 2 5 1
chris 12 1 2 3 4 5 6 7 8 9 1 2 3
john 10 8 7 6 5 4 3 2 1 7 5
jack 9 6 7 8 9 10 11 12 13 14

输出样例：

jack chris john

分析：

简单的结构体排序，利用结构体存数据，排序后输出前3位即可

坑：标签出现次数平均值就是k

代码：

#include<bits/stdc++.h>
using namespace std;
#define PII pair<int,int>const int INF = 0x3f3f3f3f;
const int N = 1e3+10;struct node{	//存 名字 不同标签的数量 标签出现次数平均值 char name[10];int num,k;const bool operator < (const node &t) const {if(t.num==num) return t.k>k;return t.num<num;}
}peo[N]; int main(){int n; scanf("%d",&n);for (int i = 0 ; i < n ; i++ ) {scanf("%s",peo[i].name);int k; scanf("%d",&k);peo[i].k = k;set<int> s;while ( k-- ){int x; scanf("%d",&x);s.insert(x);}peo[i].num = s.size();}sort(peo,peo+n);if(n>0)	printf("%s ", peo[0].name);else printf("- ");if(n>1) printf("%s ", peo[1].name);else printf("- ");if(n>2) printf("%s\n", peo[2].name);else printf("-\n");return 0;
}

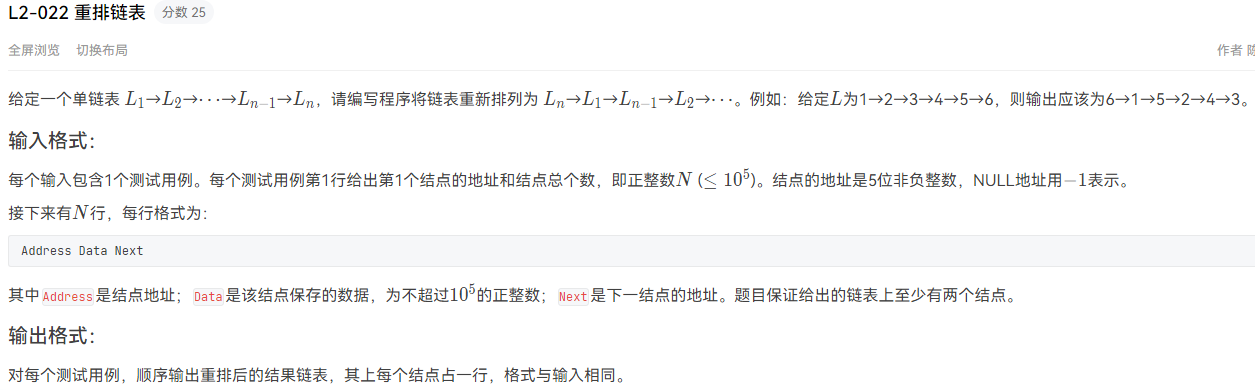
L2-022 重排链表 模拟链表

样例

输入样例：

00100 6
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218

输出样例：

68237 6 00100
00100 1 99999
99999 5 12309
12309 2 00000
00000 4 33218
33218 3 -1

分析：

用数组模拟链表，用一个指针即可实现重排输出。

坑：输入数据中可能不止一个点的下一地址为-1；

代码：

#include<bits/stdc++.h>
using namespace std;
#define PII pair<int,int>const int INF = 0x3f3f3f3f;
const int N = 1e6+10;struct node{	//存每个点的 地址 值 下一点地址 int add, data, next;
}Lnode[N];int main(){int add_s,n; scanf("%d %d", &add_s, &n);int sum=1;for( int i = 0 ; i < n ; i++ ){int a,b,c;scanf("%d %d %d", &a, &b, &c);Lnode[a].add=a;Lnode[a].data=b;Lnode[a].next=c;}vector<node> Array;	//存链表上的所有点 do{Array.push_back(Lnode[add_s]);add_s = Lnode[add_s].next;}while(add_s!=-1);int index = 0, length = Array.size() - 1;printf("%05d %d ", Array[length].add, Array[length].data);for ( int i = 0 ; i < length ; i++ ){int pos;	//pos指向当前要输出的点 if( i%2 == 0 ){pos = index;index ++;}elsepos = length-index;printf("%05d\n", Array[pos].add);printf("%05d %d ", Array[pos].add, Array[pos].data);}printf("-1\n");return 0;
}

L2-023 图着色问题 简单图

样例

输入样例：

6 8 3
2 1
1 3
4 6
2 5
2 4
5 4
5 6
3 6
4
1 2 3 3 1 2
4 5 6 6 4 5
1 2 3 4 5 6
2 3 4 2 3 4

输出样例：

Yes
Yes
No
No

分析：

简单题，存好边和点的颜色后，遍历所有边即可，用邻接表存更优。

坑：实际用的颜色和初始给出的颜色数目要一样

代码：

#include<bits/stdc++.h>
using namespace std;
#define PII pair<int,int>const int INF = 0x3f3f3f3f;
const int N = 1e3+10;vector<PII> vec;	//邻接表存边 
int col[N];			//存每个点的颜射 int main(){int v,e,k;scanf("%d%d%d", &v, &e, &k);for ( int i = 0 ; i < e ; i++ ){int x, y; scanf("%d%d", &x, &y);	vec.push_back({x,y});}int q; scanf("%d", &q);while ( q-- ){set<int> s;	//记录出现过的颜色 for ( int i = 1 ; i <= v ; i++ ){scanf("%d", &col[i]);s.insert(col[i]);}int flag = ( s.size() == k );	//统计用过的颜料 for ( int i = 0 ; i < vec.size() ; i++ )if(col[vec[i].first] == col[vec[i].second])flag = false;if ( flag ) cout<<"Yes\n";else cout<<"No\n";}return 0;
}

L2-024 部落 并查集

样例

输入样例：

4
3 10 1 2
2 3 4
4 1 5 7 8
3 9 6 4
2
10 5
3 7

输出样例：

10 2
Y
N

分析：

并查集简单题，将同一个部落的人合并和统计部落数，按要求查找并比较他们的祖先

代码：

#include<bits/stdc++.h>
using namespace std;
#define PII pair<int,int>const int INF = 0x3f3f3f3f;
const int N = 1e4+10;int fa[N];void init(int n) { for ( int i = 1 ; i <= n ; i++ ) fa[i] = i; }	//初始化 
int find(int x) { return fa[x] == x ? x : fa[x] = find( fa[x] ); }	//查找 路径压缩 
void merge(int a, int b) { a = find(a), b = find(b), fa[b] = a; }	//合并 int main(){int n; scanf("%d", &n);int m=0;	//记录编号最大的人 即 总人数 init(N);while ( n-- ) {int k, x, y ; scanf("%d%d", &k, &x);m = max(m, x);for ( int i = 1 ; i < k ; i++ ) {scanf("%d", &y);merge(x, y);	//合并 m = max(m, y);}}int ans = 0;	//计算部落数 for ( int i = 1 ; i <= m ; i++ ) if ( fa[i] == i ) ans++; printf("%d %d\n", m, ans);scanf("%d", &n);while ( n-- ){int x, y; scanf("%d %d",&x, &y);if ( find(x) == find(y) ) cout<<"Y\n";else cout<<"N\n";}return 0;
}