有序二叉树的增删改查（源代码讲解）

有序二叉树的相关实体类

TreeNode类

二叉树结点类，包含三个属性：value，leftChild，rightChild

有序二叉树类就包括这样一个根节点

剩下的getter和setter方法，有参无参构造，toString方法都是老生长谈，在这里略过不表

public class TreeNode {private int value;private TreeNode LeftChild;private TreeNode rightChild;public TreeNode(int value, TreeNode leftChild, TreeNode rightChild) {this.value = value;LeftChild = leftChild;this.rightChild = rightChild;}public TreeNode() {}public int getValue() {return value;}public void setValue(int value) {this.value = value;}@Overridepublic String toString() {return "TreeNode{" +"value=" + value +", LeftChild=" + LeftChild +", rightChild=" + rightChild +'}';}public TreeNode getLeftChild() {return LeftChild;}public void setLeftChild(TreeNode leftChild) {LeftChild = leftChild;}public TreeNode getRightChild() {return rightChild;}public void setRightChild(TreeNode rightChild) {this.rightChild = rightChild;}
}

有序二叉树类

有序二叉树只有一个属性：TreeNode root

public class BinarySearchTree {private TreeNode root;public TreeNode getRoot() {return root;}public void setRoot(TreeNode root) {this.root = root;}}

现在我们开始有序二叉树的CURD讲解

insert：有序二叉树的结点插入

比结点value值大，放右边；反之，放左边

注意结点的遍历，循环的终止条件

这个方法要放到BinarySearchTree实体类当中，作为成员方法

    // 插入public void insert(int value) {// 创建新结点TreeNode newNode = new TreeNode();newNode.setValue(value);// 若根节点为null，则新插入的结点就是根节点if (root == null) {root = newNode;return;}// 根节点不为null// index拷贝root，作为查询指针TreeNode index = root;// pre作为index的parent存在TreeNode pre = null;while (index != null) {if (value > index.getValue()) {pre = index;index = index.getRightChild();} else {pre = index;index = index.getLeftChild();}}// 此时pre指针指向的位置就是应该插入的位置，比较大小if (value > pre.getValue()) {pre.setRightChild(newNode);} else {pre.setLeftChild(newNode);}}

demo

public class TreeTest {public static void main(String[] args) {BinarySearchTree tree = new BinarySearchTree();tree.setRoot(new TreeNode(14, null, null));tree.insert(5);tree.insert(20);tree.insert(4);tree.insert(8);tree.insert(7);tree.insert(9);tree.insert(17);tree.insert(22);tree.insert(15);tree.insert(19);System.out.println(tree.getRoot());}
}

输出结果：
在这里插入图片描述

query：有序二叉树的查询

遍历查询

时间复杂度O(n)，其实就是全部结点都访问一遍来查询

二叉树的遍历

根据遍历方式优先级的不同，可以分为深度优先遍历（DFS）和广度优先遍历（BFS）

深度优先遍历

先序遍历（根左右，DLR），中序遍历（左根右，LDR）和后序遍历（左右根，LRD）

以上三种遍历，是深度优先遍历的三种形式，他们都是深度优先的

这里的D是data的意思，理解成父节点即可

这三种遍历基本都是使用递归完成，代码清晰而且很好理解，使用非递归的方式（循环+栈）也可以，在这里不做展示

先序遍历
    public void beforeSearch(TreeNode treeNode) { // DLR// 根左右// 先访问根节点，打印if (treeNode == null) {return;}// 打印根节点System.out.println(treeNode.getValue());// 再访问到最深的左结点，不打印beforeSearch(treeNode.getLeftChild());// 最后访问到最深的右结点，不打印beforeSearch(treeNode.getRightChild());}
demo
public class TreeTest {public static void main(String[] args) {BinarySearchTree tree = new BinarySearchTree();tree.setRoot(new TreeNode(14, null, null));tree.insert(5);tree.insert(20);tree.insert(4);tree.insert(8);tree.insert(7);tree.insert(9);tree.insert(17);tree.insert(22);tree.insert(15);tree.insert(19);System.out.println("=============");tree.beforeSearch(tree.getRoot());}
}

运行结果
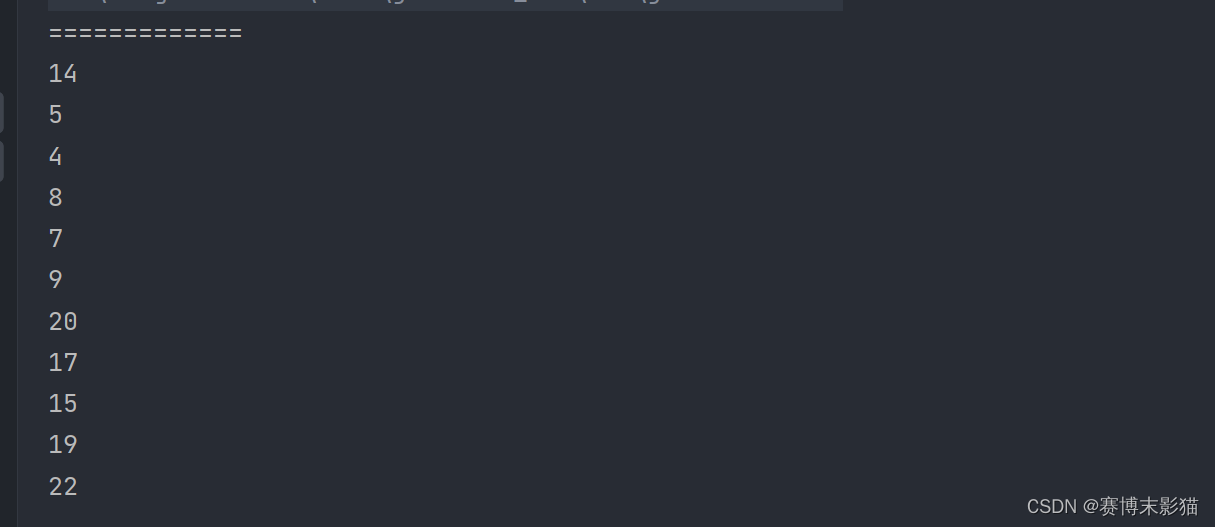
在这里插入图片描述

中序遍历
    public void middleSearch(TreeNode treeNode) {// LDR// 左根右if (treeNode == null) {return;}// 只有碰到左结点才会打印middleSearch(treeNode.getLeftChild());System.out.println(treeNode.getValue());middleSearch(treeNode.getRightChild());}
demo
public class TreeTest {public static void main(String[] args) {BinarySearchTree tree = new BinarySearchTree();tree.setRoot(new TreeNode(14, null, null));tree.insert(5);tree.insert(20);tree.insert(4);tree.insert(8);tree.insert(7);tree.insert(9);tree.insert(17);tree.insert(22);tree.insert(15);tree.insert(19);System.out.println("=============");tree.middleSearch(tree.getRoot());}
}

运行结果
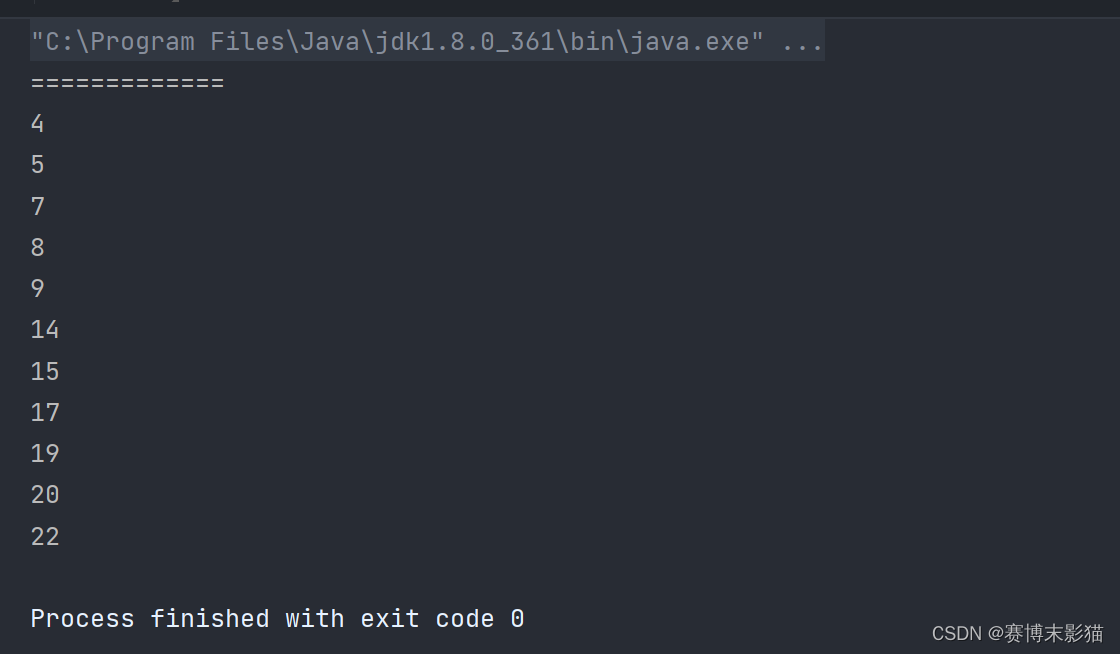
在这里插入图片描述
我们可以发现，有序二叉树中序遍历的结果，实际上就是有序二叉树从小到大排列的结果

后序遍历
    public void afterSearch(TreeNode treeNode) {// LRD//左右根if (treeNode == null) {return;}afterSearch(treeNode.getLeftChild());afterSearch(treeNode.getRightChild());System.out.println(treeNode.getValue());}
demo
public class TreeTest {public static void main(String[] args) {BinarySearchTree tree = new BinarySearchTree();tree.setRoot(new TreeNode(14, null, null));tree.insert(5);tree.insert(20);tree.insert(4);tree.insert(8);tree.insert(7);tree.insert(9);tree.insert(17);tree.insert(22);tree.insert(15);tree.insert(19);System.out.println("=============");tree.afterSearch(tree.getRoot());}
}

在这里插入图片描述

广度优秀遍历（BFS）

BFS，BreadthFirstSearch,广度优先遍历, 需要队列来辅助实现

队列的存取特点与栈相反，先进先出FIFO

public void bfs(TreeNode treeNode) {// 定义队列LinkedList<TreeNode> queue = new LinkedList<>();// 树为空直接返回if (treeNode == null) {return;}// 首先将根节点放入队列queue.add(treeNode);while (!queue.isEmpty()) {// 队列末尾节点出列treeNode = queue.pop();System.out.println(treeNode.getValue());// 左右结点放入队列if (treeNode.getLeftChild() != null) {queue.add(treeNode.getLeftChild());}if (treeNode.getRightChild() != null) {queue.add(treeNode.getRightChild());}}}

运行结果：
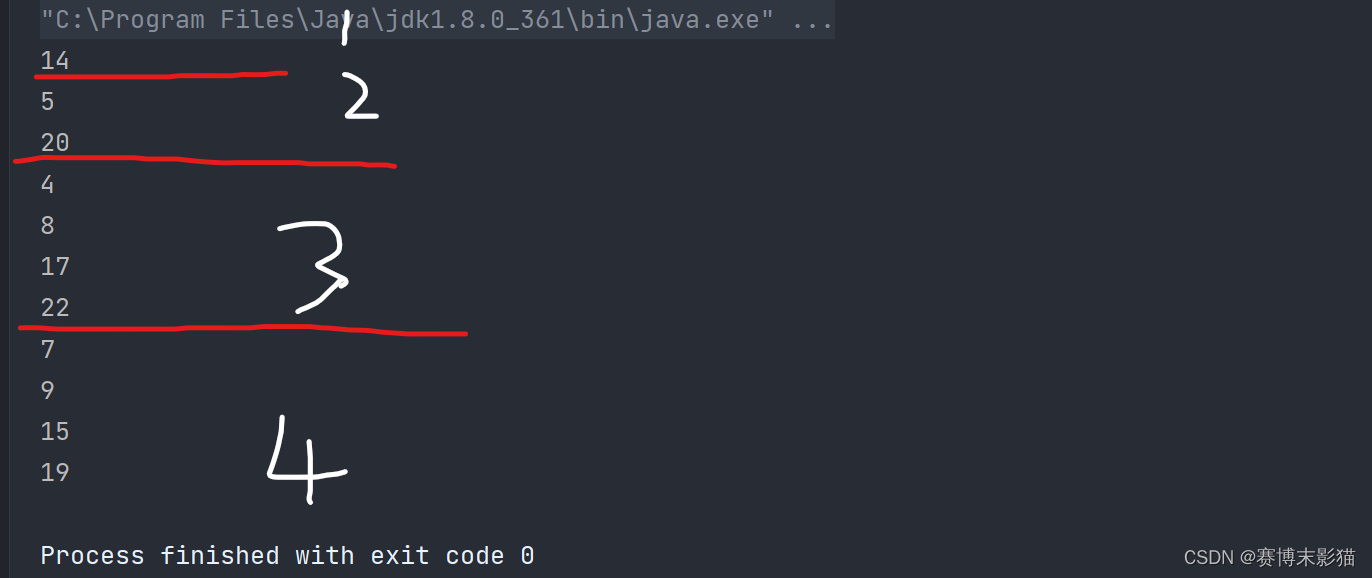
在这里插入图片描述

二分查询

时间复杂度最好O(logn)，前提是二叉树有序，而且相对平衡（否则会退化成单链表）

没什么可说的，比当前结点值大就向右遍历，反之则向左遍历

 // 二分查找public TreeNode binarySearch(TreeNode treeNode, int val) {// 复制根节点指针    		TreeNode index = treeNode;while (index != null) {if (val == index.getValue()) {System.out.println(val + "找到了");return index;	} else if (val > index.getValue()) {index = index.getRightChild();} else if (val < index.getValue()) {index = index.getLeftChild();}}return null;}

demo

public class TreeTest {public static void main(String[] args) {BinarySearchTree tree = new BinarySearchTree();tree.setRoot(new TreeNode(14, null, null));tree.insert(5);tree.insert(20);tree.insert(4);tree.insert(8);tree.insert(7);tree.insert(9);tree.insert(17);tree.insert(22);tree.insert(15);tree.insert(19);
//         二分查找System.out.println(tree.binarySearch(tree.getRoot(), 15));}
}

运行结果
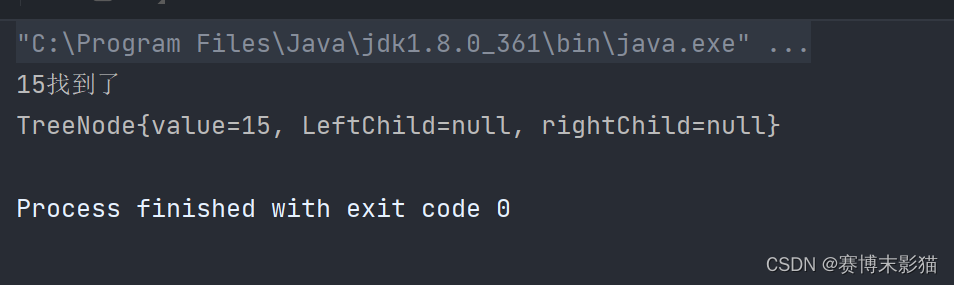
在这里插入图片描述

update：有序二叉树的编辑

有序二叉树无法直接编辑，因为编辑前后要保证有序二叉树的性质不变

所以编辑变成了删除+插入

delete：有序二叉树的删除

有序二叉树的删除操做很复杂，我们不是直接删除找到的结点，而是将其与叶子结点交换，然后删除交换后的叶子结点

如果是根节点，不允许删除；
如果是叶子结点，直接删除；
如果是中间的结点，就需要交换+删除；

这里的交换也是大有讲究

如图所示
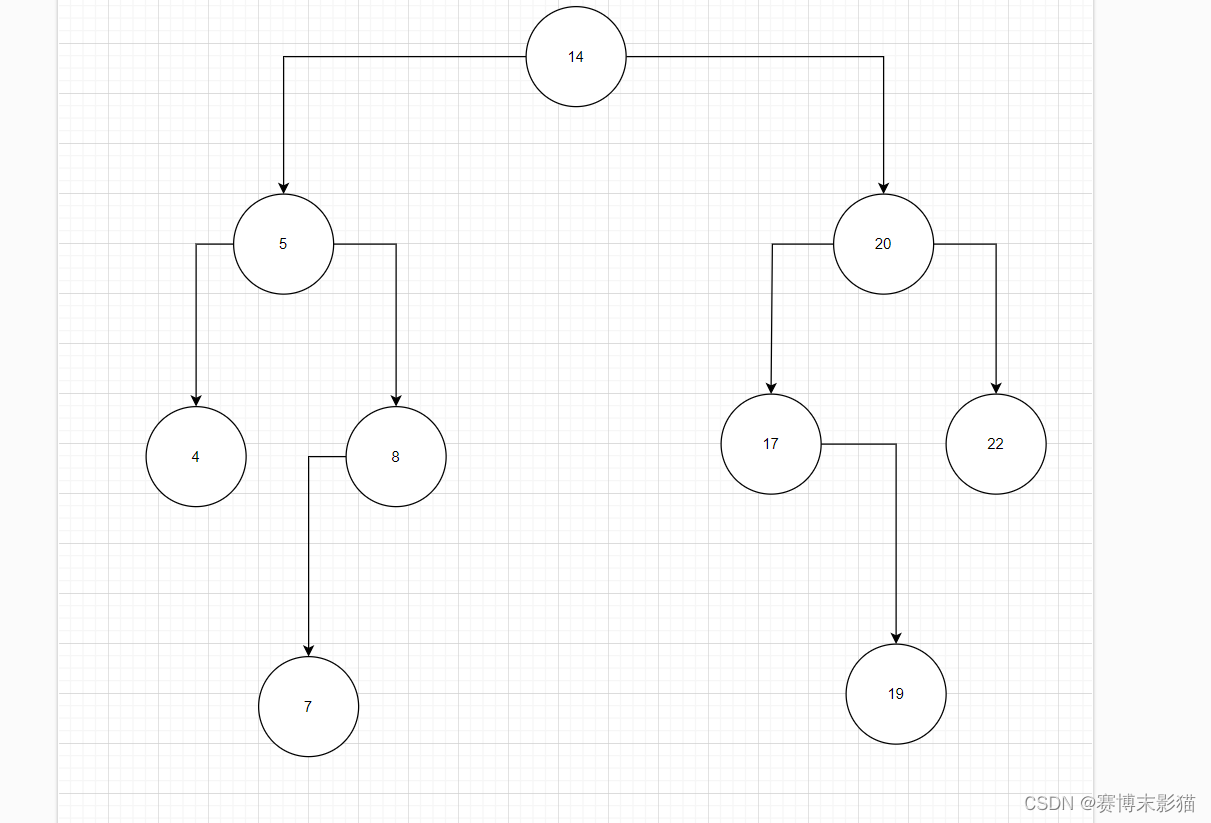
在这里插入图片描述

假设要删除结点8，我们需要找一个结点与结点8交换，然后将交换后的结点删除，要找哪个结点呢？

我们需要明白结点8的性质：比5大，比14小，我们需要重新找到一个这样的结点来替换结点8

比14小好说，只要从根节点的左子树部分找即可

比5大要怎么满足？

显然，要从结点8的右子树去寻找，右子树的每一个结点都比8大，所以肯定也比5大

但是具体是哪一个呢？

我们发现，这样的结点交换之后，依然需要满足有序二叉树的性质，如果交换的不是叶子结点，那么后续还需要新的交换

如果交换叶子节点，那么交换就会变得非常简单

结论

要删除的结点是父节点的左孩子时，就要去左孩子所在的左子树中寻找最右叶子结点去替换要删除结点；如果左子树不存在右孩子（比如只有左孩子），则直接将祖孙连接
要删除的结点是父节点的右孩子时，就要去右孩子所在的右子树中寻找最左叶子结点去替换要删除结点；如果右子树不存在左孩子（比如只有右孩子），则直接将祖孙连接

代码

// 删除: 根节点不是叶子结点的情况下不允许删除/删除叶子结点/其他结点的删除// 1. 先遍历找到结点位置，// 2. 然后判断是否存在父节点// 3. 确定要删除的结点是左子树还是右子树// 4. 根据第三步的情况删除（左子树则parent.setLeftChild(null);右子树则parent.setRightChild(null)）public void delete(TreeNode treeNode, int val) {// 为空直接返回if (treeNode == null) {return;}// 指针拷贝TreeNode index = treeNode;TreeNode parent = null;// 查询要删除的结点while (index != null) {if (val == index.getValue()) {System.out.println(val + "找到了");break;} else if (val > index.getValue()) {parent = index;index = index.getRightChild();} else if (val < index.getValue()) {parent = index;index = index.getLeftChild();}}// 找不到要删除的结点，直接返回if (index == null) {System.out.println("有序二叉树中无值为" + val + "的结点");return;}// 要删除的结点是根节点，直接返回if (parent == null) {System.out.println("根节点不允许删除");return;}// 如果index是parent的左子树，那么就去index子树当中搜索最右结点（最大结点）；若index是parent的右子树，就去找index子树中最左结点（最小结点）// 跳出循环后，index指向要删除的结点，parent指向删除结点的父节点// 分情况讨论// 情况1：index是叶子结点，直接删除if (index.getRightChild() == null && index.getLeftChild() == null) {parent.setLeftChild(null);return;}// 判断要删除结点的类型：左孩子还是右孩子        if (index.getValue() < parent.getValue()) {// 情况2：index不是叶子节点，但是右子树为空，祖孙连接if (index.getRightChild() == null) {parent.setLeftChild(index.getLeftChild());return;}// 情况3：index不是叶子节点,右子树不为空，遍历查询最右结点// 指针拷贝，标记叶子节点和叶子结点的父节点TreeNode query = index;TreeNode queryParent = parent;while (query.getRightChild() != null) {// 查询最右结点queryParent = query;query = query.getRightChild();}// 数值交换,删除叶子节点index.setValue(query.getValue());queryParent.setRightChild(null);} else {// 情况2：index不是叶子节点，但是左子树为空，祖孙连接if (index.getLeftChild() == null) {parent.setRightChild(index.getRightChild());}// 情况3：index不是叶子节点,且左子树不为空，遍历查询最左结点// 指针拷贝，标记叶子节点和叶子结点的父节点TreeNode query = index;TreeNode queryParent = parent;while (query.getLeftChild() != null) {// 查询最左结点queryParent = query;query = query.getLeftChild();}// 数值交换,删除叶子节点index.setValue(query.getValue());queryParent.setLeftChild(null);}}

demo

public class TreeTest {public static void main(String[] args) {BinarySearchTree tree = new BinarySearchTree();tree.setRoot(new TreeNode(14, null, null));tree.insert(5);tree.insert(20);tree.insert(4);tree.insert(8);tree.insert(7);tree.insert(9);tree.insert(17);tree.insert(22);tree.insert(15);tree.insert(19);tree.delete(tree.getRoot(), 14);tree.delete(tree.getRoot(), 100);tree.delete(tree.getRoot(), 5);System.out.println(tree.getRoot());}
}

运行结果：
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/814451.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

PySide6和PyQt5的show()不仅仅是展示这么简单

PySide6和PyQt5的show()不仅仅是展示这么简单

看一段代码&#xff1a; import sys from PySide6.QtWidgets import QApplication, QMainWindow, QFrameclass MainWindow(QMainWindow):def __init__(self):super().__init__()# 创建主窗口self.setWindowTitle("Main Window")self.setGeometry(100, 100, 800, 600…
阅读更多...
使用Java中的Condition+ ReentrantLock进行高效地协调线程

使用Java中的Condition+ ReentrantLock进行高效地协调线程

Condition 是 Java 中用于更细粒度的线程同步控制的一个接口&#xff0c;与传统的内置锁监视器方法&#xff08;wait(), notify(), notifyAll()&#xff09;相比&#xff0c;它提供了更高级的功能&#xff0c;允许更加灵活的线程管理。它通常与显式锁&#xff08;如 ReentrantL…
阅读更多...
使用simulink进行汽车软件建模的经验介绍

使用simulink进行汽车软件建模的经验介绍

使用Simulink进行汽车软件建模的经验介绍可以从多个方面进行阐述。首先，Simulink提供了一个强大的平台，支持车辆模型的搭建和仿真，包括但不限于商用车整车模型、自动驾驶仿真框架的构建。这表明Simulink能够满足不同自动驾驶开发任务的需求，通过选择不同的车辆、传感器模型…
阅读更多...
Redis入门到通关之Hash命令

Redis入门到通关之Hash命令

文章目录 ⛄介绍⛄命令⛄RedisTemplate API❄️❄️添加缓存❄️❄️设置过期时间(单独设置)❄️❄️添加一个Map集合❄️❄️提取所有的小key❄️❄️提取所有的value值❄️❄️根据key提取value值❄️❄️获取所有的键值对集合❄️❄️删除❄️❄️判断Hash中是否含有该值 ⛄…
阅读更多...
阐述嵌入式系统的基本组成：硬件层、驱动层、操作系统层和应用层

阐述嵌入式系统的基本组成：硬件层、驱动层、操作系统层和应用层

大家好&#xff0c;今天给大家介绍阐述嵌入式系统的基本组成&#xff1a;硬件层、驱动层、操作系统层和应用层&#xff0c;文章末尾附有分享大家一个资料包&#xff0c;差不多150多G。里面学习内容、面经、项目都比较新也比较全&#xff01;可进群免费领取。 嵌入式系统是一种能…
阅读更多...
Java集合（一）--Map（2）

Java集合（一）--Map（2）

ConcurrentHashMap与HashTable 底层实现 在JDK1.7时&#xff0c;底层采用的是分段数组&#xff0b;链表的形式&#xff0c;在JDK1.8之后&#xff0c;采用的是与HashMap相同的形式&#xff0c;数组链表/红黑树。而HashTable采用的是数组链表的形式。 如何实现线程安全 Concu…
阅读更多...
DeblurGANv2-master文件组成

DeblurGANv2-master文件组成

DeblurGANv2-master文件夹 **Config&#xff1a;**config.yaml是项目的配置文件&#xff1a;包括训练集的路径设置&#xff0c;验证集路径设置&#xff0c;对数据集内图片的处理&#xff0c;数据集增强等&#xff1b;backbone的选择&#xff0c;backbone冻结的轮数&#xff1b;…
阅读更多...
如何访问远程服务器？

如何访问远程服务器？

在现代技术时代&#xff0c;随着信息化的快速发展&#xff0c;远程访问服务器已经成为了不可或缺的一种需求。无论是企业还是个人用户&#xff0c;都需要通过远程访问来管理、传输和获取数据。本文将介绍一种名为【天联】的工具&#xff0c;它能够通过私有通道进行远程服务器访…
阅读更多...
vscode配置c\c++及美化

vscode配置c\c++及美化

文章目录 vscode配置c\c及美化1.安装vscode2.汉化3.安装c\c插件4.安装mingw5.配置mingw6. 运行c代码6.1 创建代码目录6.2 设置文件配置6.3 创建可执行任务&#xff1a;task.json6.4 编译执行6.5 再写其他代码6.6 运行多个c文件 7. 运行c文件8.调式代码8.1 创建launch.json8.2 修…
阅读更多...
【排序 贪心】3107. 使数组中位数等于 K 的最少操作数

【排序 贪心】3107. 使数组中位数等于 K 的最少操作数

算法可以发掘本质&#xff0c;如&#xff1a; 一&#xff0c;若干师傅和徒弟互有好感&#xff0c;有好感的师徒可以结对学习。师傅和徒弟都只能参加一个对子。如何让对子最多。 二&#xff0c;有无限多1X2和2X1的骨牌&#xff0c;某个棋盘若干格子坏了&#xff0c;如何在没有坏…
阅读更多...
Springboot+Vue项目-基于Java+MySQL的母婴商城系统(附源码+演示视频+LW)

Springboot+Vue项目-基于Java+MySQL的母婴商城系统(附源码+演示视频+LW)

大家好&#xff01;我是程序猿老A&#xff0c;感谢您阅读本文&#xff0c;欢迎一键三连哦。 &#x1f49e;当前专栏&#xff1a;Java毕业设计 精彩专栏推荐&#x1f447;&#x1f3fb;&#x1f447;&#x1f3fb;&#x1f447;&#x1f3fb; &#x1f380; Python毕业设计 &…
阅读更多...
TPS2041A 至 TPS2044A 、TPS2051A 至 TPS2054A

TPS2041A 至 TPS2044A 、TPS2051A 至 TPS2054A

这份文件是德州仪器&#xff08;Texas Instruments&#xff09;关于一系列电流限制型电源分配开关的数据手册&#xff0c;型号包括 TPS2041A 至 TPS2044A 和 TPS2051A 至 TPS2054A。这些开关适用于可能遇到重负载电容负载和短路的应用程序。以下是该数据手册的核心内容概要&…
阅读更多...
常用组合逻辑电路模块(5)：加法器

常用组合逻辑电路模块(5)：加法器

半加器和全加器 半加器 半加&#xff1a;只考虑两个加数本身&#xff0c;不考虑低位进位的加法运算。实现半加运算的逻辑电路称为半加器。 其对应真值表为&#xff1a; 由真值表可得逻辑表达式&#xff1a; 逻辑电路和框图如下&#xff1a; 其中&#xff0c;CO为进位输出端&…
阅读更多...
家庭网络防御系统搭建-siem之security onion 安装配置过程详解

家庭网络防御系统搭建-siem之security onion 安装配置过程详解

本文介绍一下security onion的安装流程&#xff0c;将使用该工具集中管理终端EDR和网络NDR sensor产生的日志。 充当SIEM的平台有很多&#xff0c;比如可以直接使用原生的elastic以及splunk等&#xff0c;security onion的优势在于该平台能够方便的集成网络侧&#xff08;比如…
阅读更多...
Linux 硬链接和软链接怎么区分使用？

Linux 硬链接和软链接怎么区分使用？

一、什么是硬链接和软链接 硬链接 在Linux操作系统中&#xff0c;硬链接相当于存储在硬盘驱动器中的文件&#xff0c;它实际上引用或指向硬盘驱动器上的某个点。硬链接是原始文件的镜像副本。 硬链接与软链接的区别在于&#xff0c;删除原始文件不会影响硬链接&#xff0c;但…
阅读更多...
网站如何一定程度上防止ddos和压力测试

网站如何一定程度上防止ddos和压力测试

1.通过nginx对并发数进行限制 防止压力测试的恶意攻击的思路&#xff1a;nginx限制同一个IP的并发最大为10&#xff0c;vi /usr/local/nginx/conf/nginx.conf在http{} 字段第一行添加&#xff1a;limit_conn_zone $binary_remote_addr zoneone:10m; 在对应的server{}里添加&a…
阅读更多...
AI图书推荐：如何在课堂上使用ChatGPT 进行教育

AI图书推荐：如何在课堂上使用ChatGPT 进行教育

ChatGPT是一款强大的新型人工智能&#xff0c;已向公众免费开放。现在&#xff0c;各级别的教师、教授和指导员都能利用这款革命性新技术的力量来提升教育体验。 本书提供了一个易于理解的ChatGPT解释&#xff0c;并且更重要的是&#xff0c;详述了如何在课堂上以多种不同方式…
阅读更多...
【攻防世界】supersqli（堆叠注入）

【攻防世界】supersqli（堆叠注入）

进入题目环境&#xff0c;有输入框与注入参数&#xff0c;推测类型为SQL注入&#xff1a; 测试--注入类型为数字型还是字符型&#xff0c;构造payload&#xff1a;?inject1 or 12 并提交&#xff1a; 发现页面依然正常&#xff0c;说明注入类型为字符型&#xff0c;则继续检查…
阅读更多...
ML在骨科手术术前、书中、术后方法应用综述【含数据集】

ML在骨科手术术前、书中、术后方法应用综述【含数据集】

达芬奇V手术机器人 近年来，人工智能(AI)彻底改变了人们的生活。人工智能早就在外科领域取得了突破性进展。然而，人工智能在骨科中的应用研究尚处于探索阶段。 本文综述了近年来深度学习和机器学习应用于骨科图像检测的最新成果，描述了其贡献、优势和不足。以及未来每项研究…
阅读更多...
Python数据库编程实战：sqlite3模块详解

Python数据库编程实战：sqlite3模块详解

Python数据库编程实战&#xff1a;sqlite3模块详解 在Python中&#xff0c;数据库编程是一项重要且实用的技能。通过数据库&#xff0c;我们可以高效地存储、检索和管理大量数据。Python提供了多种数据库编程接口&#xff0c;其中sqlite3模块是一个轻量级的关系型数据库引擎&a…
阅读更多...
最新文章

Copyright @ 2022~2023