Hello!这一篇主要是计算机网络中的ip地址子网划分的例题,这里例举了四个题型。保证即便从0也可以掌握!(前面是一些预备知识,不熟悉的小伙伴一定要看下学习下哦~)
这也是博主的学习过程,做题中仅仅我的理解哦。若文章中出现错误或者表述不正确或者不严谨的地方,欢迎指正呀!
最后祝愿我们每天都努力吃芝士!
预备知识
这里的预备知识是根据多为博主的博客整理而得。
ip地址
IP地址(Internet Protocol Address):互联网协议地址。IP地址是IP协议提供的一种统一的地址格式,它为互联网上的每一个网络和每一台主机分配一个逻辑地址,以此来屏蔽物理地址的差异。
通俗说,就是一个唯一标识,通信的时候需要用到。
我们为什么要使用ip地址?
在单个局域网网段中,计算机与计算机之间可以使用网络访问层提供的 MAC 地址进行通信。如果在路由式网络中,计算机之间进行通信就不能利用 MAC 地址实现数据传输了:因为 MAC 地址不能跨路由接口运行;即使强行实现跨越,使用 MAC 地址传输数据也是非常麻烦的。
这是由于内置在网卡里的固定 MAC 地址不能在地址空间上引入逻辑结构,使其无法具备真正的地址来表示国家、省、市、区、街道、路、号这类层次。因此,要进行数据传输,必须使用一种逻辑化、层次化的寻址方案对网络进行组织,这就是 IP 地址。
ip地址表示方式
IP地址采用点分十进制的表示方式
xxx.xxx.xxx.xxx
如192.168.1.1
ip地址分类
目前主要分为A、B、C、D、E五类,我们平时最常用到的是A、B、C三类
IP地址的第一位数字决定了它的类别。
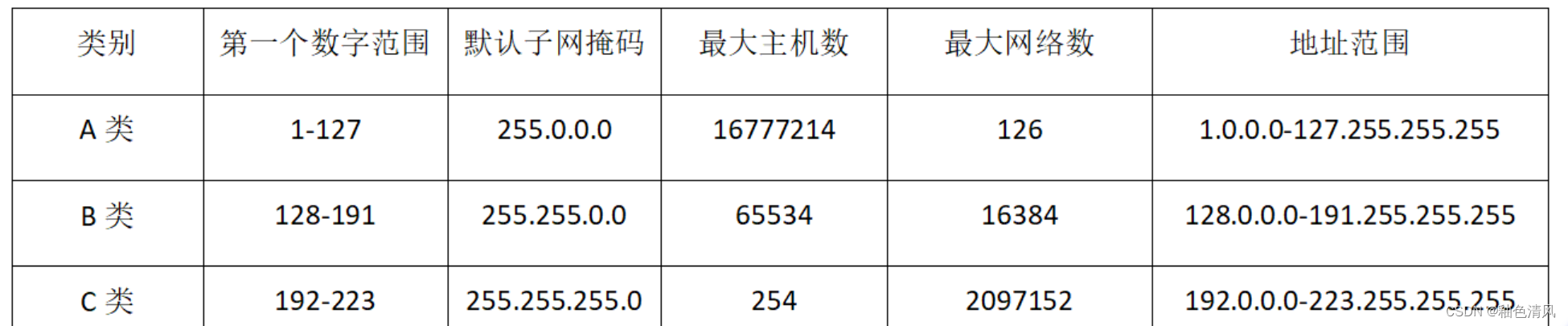

特殊的ip地址

关于子网和子网掩码

例题
在了解了上面的基础知识之后,我们接下来在运用已有知识,做几道例题。
例1
某主机IP地址为210.33.5.68,子网掩码为255.255.255.128,求其网络地址?
思路:
①我们首先要根据子网掩码得出新网络号的位数。
我们将子网掩码写成二进制形式,根据形式,很容易得出前24为都为1,128写成二进制为:10000000。
完整写成子网掩码的二进制形式为:11111111.11111111.11111111.10000000.(但是我们一般没必要全部写出来。)
②然后,我们可以根据子网掩码(网络号都为1,主机号都为0)得知,新的网络位为25。
③根据网络位即可得出这个主机的网络地址。我们知道了网络位,其实就是知道了主机位=32-25=7。(这个题不用算)
我们将这台主机的IP地址进行拆解,210、33、5不用进行拆解,它们本身就是处于网络位。只进行拆解68即可(因为这个68的二进制数字中既有网络位又有主机位)。68=64+4。故68的二进制可写为:01000100。这八位中第一位是处于网络位的,其他7位是主机位。即这个字节的第一位为网络位,是0。
④知道它的网络位后,将它的主机号,全部变为0,就可以得到它的网络地址。(将它的主机号全部变为1,就可以得到它的广播地址。)
所以这个网络地址即为:210.33.5.0。
例2
某A类网络20.0.0.0的子网掩码为255.224.0.0,请确定它可以划分子网的个数,写出每个子网的子网号。
思路:
①同样,我们将子网掩码进行拆解,得到新网络号的网络位。

我们可以根据题目可知这是一个A类网络,然后子网划分时,第二个字节的前三位变成了子网号。这样这三位和原来的第一个字节一起组成了新的网络号。
因为是三位,所以我们可以得出子网的个数为8。

下面我们分别列出这八个不同的子网,并写出其网络号,并写出其网络地址。

例3
将某 C类网200.161.30.0划分成4个子网,请计算出每个子网的有效的主机IP地址范围和对应的子网掩码。
思路:
首先,我们知道C类网的前三个字节为网络号,最后一个字节为主机号。在进行子网划分时,我们就是要选取主机号的某几位作为子网号,与原来的网络号一起组成新的网络号。
因为题目中给出了,划分成4个子网,所以最后一个字节中的前两位作为子网号。
题目让我们计算子网掩码即:

下面,我们一起来计算每个子网的有效IP地址。
首先,我们一依次列出这4个不同的子网,写出其子网号,并写出其网络地址。然后再子网号的基础上加上63(32+16+8+4+2+1)得出广播地址。
这样我们就得出了各个子网的的IP地址的边界值。

但是题目中让我们给出有效的主机IP地址的范围,需要去掉每个子网的网络地址和广播地址,从而得出范围,即:

例4
某公司申请到的网络地址为192.3.2.0,现要划分5个子公司,最大的子公司有28台计算机,每一个公司在一个子网中。
则:
(1)子网掩码应为多少?
(2)5个子公司的网络地址分别是多少?
思路:
首先,我们可以根据 28 、5 这两个数字看如何划分。
首先,我们可以假定划分子网数为8,那么主机位剩余8-3=5位,每个子网可分配的的子网号为32-2=30.
恰好符合题意。
然后,我们写出子网掩码:

第二问让我们写出五个子公司的网络地址。
我们的分配可以得到8个网络号,即8个子网。所以我们任意选取其中五个就好了,得出相应的网络地址。


)









)



)
![[C++][算法基础]n-皇后问题(DFS)](http://pic.xiahunao.cn/[C++][算法基础]n-皇后问题(DFS))


