题目
小明目前在做一份毕业旅行的规划。
打算从北京出发,分别去若干个城市,然后再回到北京,每个城市之间均乘坐高铁,且每个城市只去一次。
由于经费有限,小明希望能够通过合理的路线安排尽可能的省些路上的花销。
给定一组城市和每对城市之间的火车票的价钱,找到每个城市只访问一次并返回起点的最小车费花销。
注意:北京为 1号城市。
输入格式
第一行包含一个正整数 n,表示城市个数。
接下来输入一个 n 行 n列的矩阵,表示城市间的车票价钱。
输出格式
输出一个整数,表示最小车费花销。
数据范围
1<n≤20
包括北京
车票价格均不超过 1000元。
- 输入样例:
4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
- 输出样例:
13
说明
共 4个城市,城市 1和城市 1的车费为 0,城市 1和城市 2之间的车费为 2,城市 1和城市 3之间车费为 6,城市 1和城市 4之间的车费为 5,以此类推。
假设任意两个城市之间均有单程票可买,且价格均在 1000元以内,无需考虑极端情况。
题解
import java.util.Arrays;
import java.util.Scanner;/*** @author akuya* @create 2024-04-01-20:00*/
public class Main {static int N=20;static int M=1<<N;static int n;static int INF=0x3f3f3f3f;static int w[][]=new int[N][N];// f[i][j]:当前走过的城市状态为 i,且最后一个停留的城市是 j的最小花费static int f[][]=new int[M][N];
; public static void main(String[] args) {Scanner scanner =new Scanner(System.in);n=scanner.nextInt();for(int i=0;i<n;i++){for(int j=0;j<n;j++)w[i][j]=scanner.nextInt();}for(int i=0;i<M;i++){Arrays.fill(f[i],INF);}f[1][0]=0;// 开始在 0号点,状态集合是 000..001(最后一个点是0),合法状态for(int i=1;i<1<<n;i+=2){for(int j=0;j<n;j++){if((i>>j&1)==1){for(int k=0;k<n;k++){if((((i-(1<<j))>>k)&1)==1){//i去掉第 j位后还有第 k位// ..... -> k -> j 经过 k之后再经过 jf[i][j]=Math.min(f[i][j],f[i-(1<<j)][k]+w[k][j]);}}}}}int res=INF;for(int i=1;i<n;i++){// 最后一定是f[111...1111][?] ?是除了 0以外的点res=Math.min(res,f[(1<<n)-1][i]+w[i][0]);}System.out.println(res);}
}思路
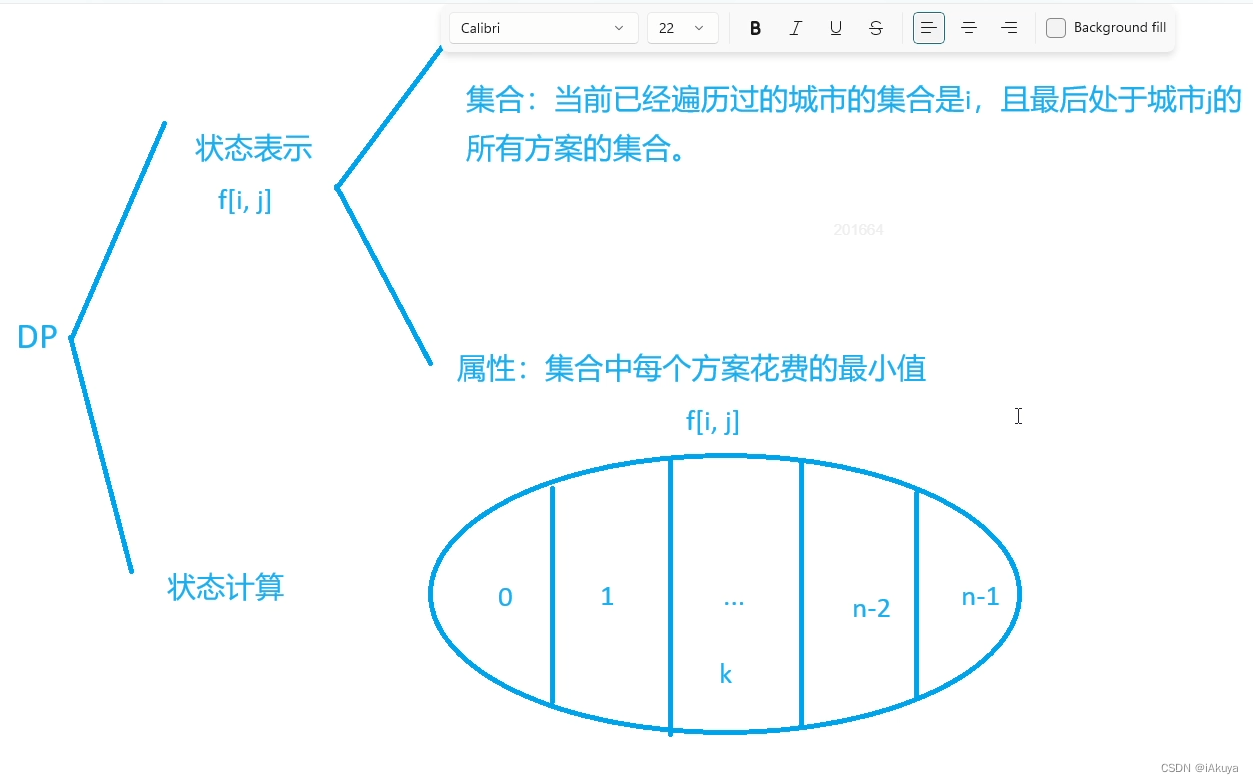
这道题是一道典型的动态规划问题,但如何设计状态数组是个问题,根据经验,没错根据经验,动态规划问题的状态数组的设计需要经验,这个靠刷题积累,这道题采用状态压缩来设计状态数组,具体如下图。i为当前已经走过的城市,j为目前所在的城市。


)



)




)







