2369. 检查数组是否存在有效划分

思路：

1.状态定义:f[i]代表考虑将[0,i]是否能被有效划分，有则为true，没有则为false

2.状态转移:f[i]的转移有3种可能：
1 由f[i-2]转移过来，且nums[i-1] == nums[i]
2 由f[i-3]转移过来，且nums[i-2] == nums[i-1] == nums[i]
3 由f[i-3]转移过来，且nums[i-1] == nums[i-2]+1;nums[i]==nums[i-1]+1

3.初始化:f[0]=false，f[1]=nums[0]== nums[1]，f[2]=nums[0] == nums[1]==nums[2]||递增

4.遍历顺序:正序遍历[3,n-1]

5.返回形式:返回f[n-1]

代码：

   public boolean validPartition(int[] nums) {int n = nums.length;boolean[] f = new boolean[n];f[0] = false;f[1] = nums[0] == nums[1];if (n == 2) return f[1];f[2] = (nums[0] == nums[1] && nums[1] == nums[2]) || (nums[1] == nums[0] + 1 && nums[2] == nums[1] + 1);for (int i = 3; i < n; i++) {boolean b1 = f[i - 2] && nums[i - 1] == nums[i];boolean b2 = f[i - 3] && nums[i - 2] == nums[i - 1] && nums[i - 1] == nums[i];boolean b3 = f[i - 3] && nums[i - 1] == nums[i - 2] + 1 && nums[i] == nums[i - 1] + 1 ;f[i] = b1 || b2 || b3;}return f[n - 1];}

1976. 到达目的地的方案数

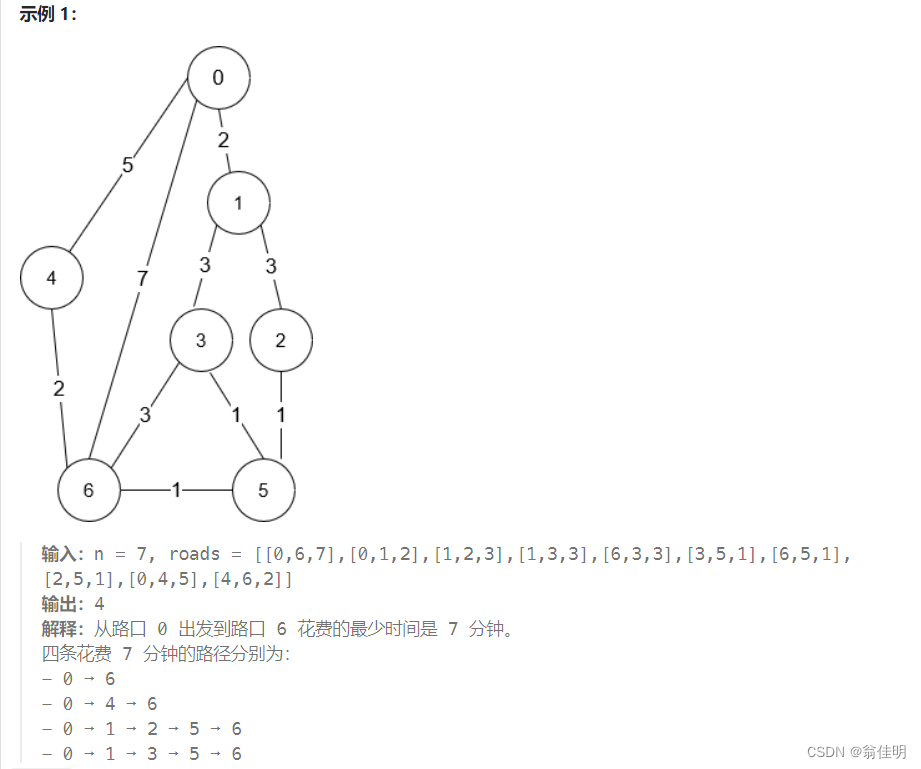
思路：

利用 Dijkstra 算法计算最短路径，并同时记录最短路径的数量，以解决从起点到终点的最短路径数量的问题

1. 使用邻接矩阵 g 存储节点之间的距离，其中 g[x][y] 表示节点 x 到节点 y 的距离，因为是无向图，所以 g[y][x] 也表示相同的距离。
2. 初始化距离数组 dis 和路径数量数组 f。dis 存储从起点到每个节点的最短距离，f 存储从起点到每个节点的最短路径数量。
3. 根据 Dijkstra 算法的思想，不断更新未确定最短路径长度的节点，直到找到从起点到终点的最短路径。
4. 在更新节点的过程中，根据新的距离和之前求得的最短距离的比较，更新最短路径长度和路径数量。如果发现新的最短路径或者相同长度的最短路径，就更新路径数量。
5. 当找到从起点到终点的最短路径时，返回终点的最短路径数量。

代码：

//1976. 到达目的地的方案数--Dijkstrapublic int countPaths(int n, int[][] roads) {long[][] g = new long[n][n]; // 邻接矩阵，用于存储节点之间的距离for (long[] row : g) {Arrays.fill(row, Long.MAX_VALUE / 2); // 初始化邻接矩阵，将所有距离设置为一个较大的值以防止溢出}for (int[] r : roads) {int x = r[0];int y = r[1];int d = r[2];g[x][y] = d; // 将节点x和节点y之间的距离设置为dg[y][x] = d; // 因为是无向图，所以节点x和节点y之间的距离相同}long[] dis = new long[n]; // 存储从起点到每个节点的最短距离Arrays.fill(dis, 1, n, Long.MAX_VALUE / 2); // 初始化dis数组，将除起点外的距离设置为一个较大的值以防止溢出int[] f = new int[n]; // 存储从起点到每个节点的最短路径数量f[0] = 1; // 起点到自身的最短路径数量为1boolean[] done = new boolean[n]; // 标记节点是否已经确定最短路径长度while (true) {int x = -1;for (int i = 0; i < n; i++) {if (!done[i] && (x < 0 || dis[i] < dis[x])) {x = i; // 找到未确定最短路径长度的节点中距离最小的节点}}if (x == n - 1) {// 如果最小距离的节点是终点，那么已经找到了从起点到终点的最短路径// 不可能找到比 dis[n-1] 更短，或者一样短的最短路了（注意本题边权都是正数）return f[n - 1]; // 返回起点到终点的最短路径数量}done[x] = true; // 最短路径长度已确定（无法变得更小）for (int y = 0; y < n; y++) { // 尝试更新节点x的邻居的最短路径long newDis = dis[x] + g[x][y]; // 计算从起点经过节点x到达节点y的距离if (newDis < dis[y]) {// 如果新的距离比之前求得的最短距离更小，说明发现了一条更新的最短路径dis[y] = newDis; // 更新节点y的最短路径长度f[y] = f[x]; // 节点y的最短路径数量等于节点x的最短路径数量} else if (newDis == dis[y]) {// 如果新的距离和之前求得的最短距离一样长，说明找到了一条相同长度的最短路径f[y] = (f[y] + f[x]) % 1_000_000_007; // 更新节点y的最短路径数量，累加节点x的最短路径数量}}}}

2917. 找出数组中的 K-or 值

思路：

1.因为0 <= nums[i] < 2 ^31，最多考虑 31 位

2.遍历每一位，统计当前位为1的元素个数

3.将x右移i位，如果当前位上的数为1，和1相与得1。为0，和1相与为0，用count1计数

4.如果当前位1的元素个数大于等于 k，则将该位设为1

5.将1左移位，再进行按位或运算，将ans的该位置设为1，最后直接返回ans

代码：

   // 2917. 找出数组中的 K-or 值public int findKOr(int[] nums, int k) {int ans = 0;for(int i = 0;i<31;i++){// 遍历每一位，最多考虑 31 位（int 型）int count1 = 0;// 统计当前位为1的元素个数for(int x:nums){count1 += x>>i&1;}// 如果当前位1的元素个数大于等于 k，则将该位设为1if(count1>=k){ans |= 1<<i;}}return ans;}

2575. 找出字符串的可整除数组

思路：

1.因为给出了范围：1 <= m <= 10^9,所以，在进行模运算的时候，要注意是否超出范围

2.在这里，要采用long来运算，超过10^9（十亿）开long, int的范围到2^31-1，差不多二十亿~

3.遍历字符串，取到的字符进行模运算

4.最后通过三目运算符来判断div各下标的值

代码：

    //2575. 找出字符串的可整除数组public int[] divisibilityArray(String word, int m) {long temp = 0;int[] div = new int[word.length()];for (int i = 0; i < word.length(); i++) {temp = (temp * 10 + word.charAt(i) - '0') % m;div[i] = temp == 0 ? 1 : 0;}return div;}

2834. 找出美丽数组的最小和

思路：

1.n 是数组的长度。k 是题目中的target。m 的值是通过取k / 2和n的较小值来计算的，这是因为当选取的数字超过k / 2时，可能会存在两个数加起来等于k的情况。

2.计算从1加到m的和，即m * (m + 1) / 2。在这个范围内的任意两个数相加都不会等于k

3.计算剩余部分的和(n - m - 1 + k * 2) * (n - m) / 2

4.最后，对结果取模1_000_000_007

代码：

public int minimumPossibleSum(int n, int k) {long m = Math.min(k / 2, n);return (int) ((m * (m + 1) + (n - m - 1 + k * 2) * (n - m)) / 2 % 1_000_000_007);
}

299. 猜数字游戏

思路：

1. 遍历两个字符串 secret 和 guess，若字符既在相同位置上又相等，则位置和数字都正确，对应的 a 值加一。
2. 若字符在不同位置但相等，则统计每个数字出现的次数，分别存储在 cntS 和 cntG 数组中。
3. 最后再遍历 0 到 9 的所有数字，取 cntS[i] 和 cntG[i] 中较小的一个，累加起来就是数字正确但位置不对的个数，即 b 值。
4. 最终返回 a + "A" + b + "B"，表示猜中的数字个数和位置都正确的数量以及数字正确但位置不对的数量。

代码：

// 猜数字游戏
public String getHint(String secret, String guess) {int a = 0; // 位置和数字都正确的个数int[] cntS = new int[10]; // 存储secret中各个数字出现的次数int[] cntG = new int[10]; // 存储guess中各个数字出现的次数for (int i = 0; i < secret.length(); i++) {if (secret.charAt(i) == guess.charAt(i)) {a++; // 若位置和数字都正确，则a加1} else {cntS[secret.charAt(i) - '0']++; // 统计secret中各个数字出现的次数cntG[guess.charAt(i) - '0']++; // 统计guess中各个数字出现的次数}}int b = 0; // 数字正确但位置不对的个数for (int i = 0; i < 10; i++) {b += Math.min(cntS[i], cntG[i]); // 统计数字正确但位置不对的个数}return a + "A" + b + "B"; // 返回结果字符串
}

2129. 将标题首字母大写

思路：

1.先根据空格，将每个单词切割，依次遍历

2.用StringBuilder来对结构进行拼接

3.如果StringBuilder不是空的，最后面直接添加一个空格（还原空格）

4.如果该单词大于2，将该单词的首字母分割下来转为大写。将剩余部分覆盖

5.将剩余部分转化为小写，最后返回一个字符串

代码：

//2129. 将标题首字母大写public String capitalizeTitle(String title) {StringBuilder ans = new StringBuilder();for (String s:title.split(" ")) {if (ans.length()!=0){ans.append(' ');}if (s.length()>2){ans.append(s.substring(0,1).toUpperCase());s= s.substring(1);}ans.append(s.toLowerCase());}return ans.toString();}

1261. 在受污染的二叉树中查找元素

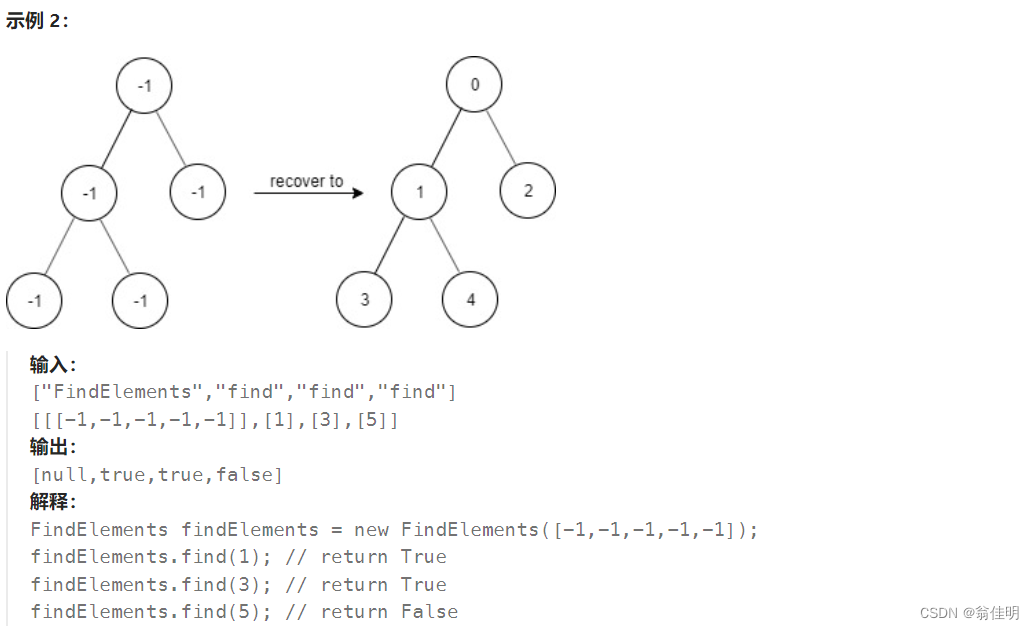
思路：

1.在dfs中传入结点和对应的值，对根节点的左树和右树依次遍历

2.在递归的过程中，通过传进的参数进行运算，修改val，并存入Hash表中

3.最终在哈希表中查看是否存在target

代码：

    //1261. 在受污染的二叉树中查找元素private  final Set<Integer>set = new HashSet<>();public  FindElements(TreeNode root) {dfs(root,0);}public boolean find(int target) {return set.contains(target);}private void dfs(TreeNode node,int val){if (node==null){return;}set.add(val);dfs(node.left,val*2+1);dfs(node.right,val*2+2);}

2864. 最大二进制奇数

思路：

1.拼贴字符串。

2.遍历字符串s,统计1的个数。

3.如果只有一个1，将1放在末尾，保证这个二进制数是奇数

4.如果有多个1，将一个1放在末尾，将剩余的1尽可能的放在开头

5.用StringBuilder来拼接字符，最后返回一个字符串的形式

代码1：

    public String maximumOddBinaryNumber(String s) {int count = 0;StringBuilder sb = new StringBuilder();for (int i = 0; i < s.length(); i++) {count += s.charAt(i)-'0';}if (count == 0) {for (int i = 0; i < s.length() - 1; i++) {sb.append(0);}sb.append(1);} else {for (int i = 0; i < count - 1; i++) {sb.append(1);}for (int i = 0; i < s.length() - count; i++) {sb.append(0);}sb.append(1);}return sb.toString();}

2789. 合并后数组中的最大元素

思虑：

1.因为要合并的条件之一是，num[i]<=num[i+1].所以将最后一个元素当做初始的值

2.从倒数第二个元素开始遍历，不断进行合并后面的元素

3.直到发现num[i]的元素，要大于后面所有合并的值，将合并的最大值更新为此时的num[i]

4.重新开始遍历合并。

代码：

    public long maxArrayValue(int[] nums) {int n = nums.length;long sum = nums[n - 1];for (int i = n - 2; i >= 0; i--) {if (nums[i] <= sum) {sum += nums[i];}else {sum = nums[i];}}return (long) sum;}

2312. 卖木头块

思路1:用DFS进行记忆化搜索

1.要用DFS深度优先遍历每一种情况。在递归的同时，不断更新得到的最大值，作为该方案的答案。保存在f中

2.因为在深度优先遍历的时候会重复，所以递归的结束的条件为，f有记录，返回该几率。如果为空，进行答案的计算

3.首先要根据给出的初始模板的宽和高，确定存储价格的d数组，和存储方法价格的f数组的大小

4.遍历prices数组，将得到的价格存储到d中。

5.进行DFS记忆化搜索。不仅要跟新从高切割的各种可能性，还要更新从款切割的可能性。

代码：

    private int[][] d;private Long[][] f;public long sellingWood(int m, int n, int[][] prices) {d = new int[m + 1][n + 1];//d存的是对应的价格f = new Long[m + 1][n + 1];//f存答案//设置二维数组的大小for (int[] var : prices) {d[var[0]][var[1]] = var[2];}//遍历price数组，将每一块宽和高所对应的价格存进d中//return dfs(m, n);//进行深度优先遍历，计算钱数}private long dfs(int h, int w) {if (f[h][w] != null) {return f[h][w];}//如果高和宽已经被计算过了，直接返回long ans = d[h][w];for (int i = 1; i < h / 2 + 1; i++) {ans = Math.max(ans, dfs(i, w) + dfs(h - i, w));}for (int i = 1; i < w / 2 + 1; i++) {ans = Math.max(ans, dfs(h, i) + dfs(h, w - i));}return f[h][w] = ans;}

思路2:动态规划

代码：

    public long sellingWood(int m, int n, int[][] prices) {int[][] d = new int[m + 1][n + 1];long[][] f = new long[m + 1][n + 1];for (int[] var : prices) {d[var[0]][var[1]] = var[2];}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {f[i][j] = d[i][j];for (int k = 1; k < i; k++) {f[i][j] = Math.max(f[i][j], f[k][j] + f[i - k][j]);}for (int k = 1; k < j; k++) {f[i][j] = Math.max(f[i][j], f[i][k] + f[i][j - k]);}}}return f[m][n];}

2684. 矩阵中移动的最大次数

思虑：

1.将第一列的所有行坐标，用IntStream 来生成一个范围 [0, m) 内的整数流，用boxed方法进行装箱，并收集到Set集合中

2.从第一列开始，逐列进行遍历。

3.每一列，将集合中的所有行坐标取出，对每一个行坐标x,找出下一列可能满足的行坐标x，并且下一步要大

4.将符合的行坐标加入集合t,如果不能移动，返回当前列数

5.否则将t赋值給q,继续下一次的遍历

6.最后如果都遍历完了，说明走到最后一列,返回n-1

代码：

    public int maxMoves(int[][] grid) {int m = grid.length;int n = grid[0].length;Set<Integer> q = IntStream.range(0, m).boxed().collect(Collectors.toSet());//使用 Java 8 中的 IntStream 来生成一个范围在// [0, m) 内的整数流，然后通过 boxed() 方法将 IntStream 装箱为// Stream<Integer>，最后通过collect(Collectors.toSet()) 方法// 将整数流中的元素收集到一个 Set 集合中。for (int j = 0; j < n - 1; j++) {Set<Integer> t = new HashSet<>();for (int x : q) {for (int i = x - 1; i <= x + 1; i++) {if (i >= 0 && i < m && grid[x][j] < grid[i][j]) {t.add(i);}}}if (t.isEmpty()){return j;}q = t;}return n-1;//最后如果都遍历完了，说明走到最后一列,返回n-1}

310. 最小高度树

思路：拓扑排序

1. 首先判断节点数量n，如果只有一个节点，则直接返回该节点作为最小高度树的根节点。
2. 构建邻接表g和度数数组degree：
   • 使用邻接表g存储每个节点的相邻节点。
   • 使用度数数组degree存储每个节点的度数（即相邻节点的数量）。
3. 遍历边数组edges，构建邻接表g和更新度数数组degree：
   • 对于每条边[e[0], e[1]]，将节点e[0]与节点e[1]互相添加到各自的邻接表中，同时更新它们的度数。
4. 初始化队列q，并将所有叶子节点（度数为1的节点）加入队列：
   • 遍历所有节点，将度数为1的节点加入队列q。
5. 使用BFS遍历叶子节点层级，不断更新度数并将新的叶子节点加入队列：
   • 从队列中取出当前层级的叶子节点，更新其相邻节点的度数。
   • 若相邻节点的度数更新为1，则将其加入队列q。
6. 最终队列中剩下的节点即为最小高度树的根节点列表，将其返回作为结果。

代码：

class Solution {public List<Integer> findMinHeightTrees(int n, int[][] edges) {// 如果只有一个节点，直接返回该节点if (n == 1) {return List.of(0);}// 构建邻接表List<Integer>[] g = new List[n];Arrays.setAll(g, k -> new ArrayList<>());int[] degree = new int[n]; // 存储每个节点的度数for (int[] e : edges) {int a = e[0], b = e[1];g[a].add(b);g[b].add(a);++degree[a];++degree[b];}Deque<Integer> q = new ArrayDeque<>();// 将所有叶子节点（度数为1）加入队列for (int i = 0; i < n; ++i) {if (degree[i] == 1) {q.offer(i);}}List<Integer> ans = new ArrayList<>();while (!q.isEmpty()) {ans.clear(); // 清空结果列表// 遍历当前层的节点for (int i = q.size(); i > 0; --i) {int a = q.poll();ans.add(a); // 将当前节点加入结果列表// 更新与当前节点相邻的节点的度数for (int b : g[a]) {if (--degree[b] == 1) {q.offer(b); // 若更新后度数为1，则加入队列}}}}return ans; // 返回最终结果列表}
}

303. 区域和检索 - 数组不可变

思路：前缀和

1.因为要根据给出的两个索引，来返回索引区间的和

2.创建一个n+1大小的新数组

3.遍历原本的数组，计算每个位置的前缀和

4.再通过给出的索引下标，在新数组中，找到两个索引的前缀和

5.返回两者的差值

6.left位置的前缀和，不包含left。right位置的前缀和，不包含right。所以要right+1

代码：

public  NumArray(int[] nums) {int n = nums.length;sum = new int[n + 1];for (int i = 0; i < n; i++) {sum[i + 1] = sum[i] + nums[i];}}public int sumRange(int left, int right) {return sum[right + 1] - sum[left];}

1793. 好子数组的最大分数

思路：单调栈

1遍历数组，用单调栈来找到该位置左边比该位置小的数，存储进数组left中

2.清空栈，再找该位置右边比该位置小的数，存储进数组right中

3 遍历每个位置，计算以当前位置元素为中心时的得分，并找出最大得分。

代码：

class Solution {public int maximumScore(int[] nums, int k) {// 单调栈int n = nums.length;int[] left = new int[n];Deque<Integer> stack = new ArrayDeque<>();// 构建左边第一个比当前元素小的索引for (int i = 0; i < n; i++) {int x = nums[i];while (!stack.isEmpty() && x <= nums[stack.peek()]) {stack.pop();}left[i] = stack.isEmpty() ? -1 : stack.peek();stack.push(i);}stack.clear();int[] right = new int[n];// 构建右边第一个比当前元素小的索引for (int i = n - 1; i >= 0; i--) {int x = nums[i];while (!stack.isEmpty() && x <= nums[stack.peek()]) {stack.pop();}right[i] = stack.isEmpty() ? n : stack.peek();stack.push(i);}int ans = 0;// 计算每个位置得分并找出最大得分for (int i = 0; i < n; i++) {int min = nums[i];int l = left[i];int r = right[i];if (l < k && k < r) {ans = Math.max(ans, min * (r - l - 1));}}return ans;}
}

518. 零钱兑换 II

思路：

1. 在change方法中，首先将coins数组赋值给成员变量this.coins，并初始化一个二维数组memo用于记忆化搜索。然后调用dfs1方法进行深度优先搜索，并返回结果。
2. dfs1方法是递归实现的动态规划函数。它接受两个参数i和c，分别表示当前考虑的硬币种类索引和剩余需凑成的金额。
3. 在dfs1方法中，首先判断基本情况：如果i<0，表示已经没有硬币可选，这时如果c为0，则返回-1表示找到一种组合方式；否则返回0表示无法凑成目标金额。这是一种特殊情况的处理，因为硬币用完了但金额却正好凑成了，需要用-1来区分。
4. 接着检查记忆化数组memo[i][c]，如果已经计算过，则直接返回记忆结果。
5. 如果当前硬币面值大于剩余金额c，那么无法选择当前硬币，直接返回dfs1(i-1, c)，表示不选择当前硬币，考虑下一个硬币。
6. 否则，当前硬币可以选择，递归计算选择当前硬币和不选择当前硬币两种情况下的组合数量，并将结果存入记忆数组memo[i][c]中，然后返回该结果。
7. 最后，在change方法中返回dfs1(n-1, amount)，表示使用前n种硬币凑成总金额amount的组合数量。

代码：

//518. 零钱兑换 IIprivate int[] coins;private int[][] memo;public int change(int amount, int[] coins) {this.coins = coins;int n = coins.length;memo = new int[n][amount + 1];for (int[] row : memo) {Arrays.fill(row, -1);}return dfs1(n - 1, amount);}private int dfs1(int i, int c) {if (i < 0) {return c == 0 ? -1 : 0;}if (memo[i][c] != -1) {return memo[i][c];}if (c < coins[i]) {return memo[i][c] = dfs1(i-1,c);}return memo[i][c] = dfs1(i-1,c)+dfs1(i,c-coins[i]);}

2580. 统计将重叠区间合并成组的方案数

思路：

合并区间，推理可得。方案数和区间数的关系为 2的幂次

1.首先，对每个子数组的第一个元素进行排序

2.按照顺序，遍历数组

3.如果此时，该数组的开始范围，大于目前的最大范围，区间数加一，更新方案数

4.目前最大值和当前数组末尾取最大值

代码：

    public int countWays(int[][] ranges) {Arrays.sort(ranges,(a,b)->a[0]-b[0]);int ans = 1;int maxR = -1;for (int[] range : ranges) {if (range[0] > maxR) {ans = ans * 2% 1_000_000_007;}maxR  = Math.max(maxR,range[1]);}return ans ;}

1997. 访问完所有房间的第一天

思路：

1.首先，初次访问算奇数次，必然会返回前面的房间。叫做回访

2.如果访问次数是偶数次，则可以访问下一个房间

3.回访之后，当前回访的访问次数变为奇数次，仍要进行回访，直到返回后，变为偶数次。

4.动态方程为：到达i的天数 = 第一次到达i-1的天数+1天回退+回退后重新到达i-1的天数+向后拜访1天

​

代码：

    //动态规划public int firstDayBeenInAllRooms(int[] nextVisit) {int n = nextVisit.length;long[] f = new long[n];final int mod = (int) 1e9 + 7;for (int i = 1; i < n; i++) {f[i] = (f[i - 1] + 1 + f[i - 1] - f[nextVisit[i - 1]] + 1+mod)%mod;//加上mod再去模，为了防止出现负数}return (int) f[n-1];}

331. 验证二叉树的前序序列化

思路：

1.用栈来存储

2.如果栈顶遇到两个空节点，并且第三不为空。将这三个换成一个空节点

3.相当于用两个空节点，换掉叶子结点，这个叶子结点看成空节点

4.最后，如果是二叉树，栈的大小只能为1，并且最终被换成了空节点

代码：

    public boolean isValidSerialization(String preorder) {List<String> stark = new ArrayList<>();for (String x : preorder.split(",")) {stark.add(x);while (stark.size() >= 3 &&stark.get(stark.size() - 1).equals("#") &&stark.get(stark.size() - 2).equals("#") &&!stark.get(stark.size() - 3).equals("#")) {stark.remove(stark.size() - 1);stark.remove(stark.size() - 1);stark.remove(stark.size() - 1);stark.add("#");}}return stark.size() == 1 && stark.get(0).equals("#");}

点击移步博客主页，欢迎光临~