39. 组合总和 

39. 组合总和 - 力扣（LeetCode）

代码随想录 (programmercarl.com)

带你学透回溯算法-组合总和（对应「leetcode」力扣题目：39.组合总和）| 回溯法精讲！_哔哩哔哩_bilibili

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates =[2,3,6,7],target =7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5],target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2],
target = 1
输出: []

提示：

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素 互不相同
• 1 <= target <= 40

 第一反应这个题和昨天的相差不大，还是用回溯法，只不过target中的数字可以重复使用。那这一条件的改变会影响哪里呢？自己画了图：

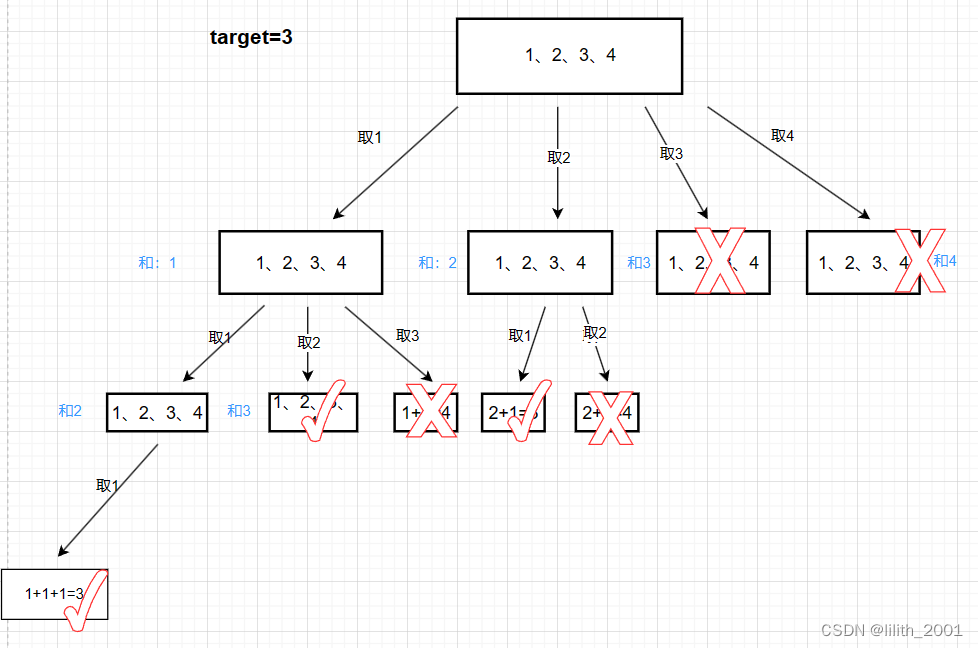
回溯算法模板：

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

回溯三部曲：

1、确定参数： 定义一个二位数组result存放结果集，一个path存放符合条件的结果。

public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {}

2、确定终止条件：从上图中可以看到，sum>target或者sum=target的时候终止，sum=target时还要把path返回结果集

if(sum > target){return;
}
if (sum == target) {res.add(new ArrayList<>(path));return;
}

3、确定单层遍历逻辑：

for (int i = startIndex; i < candidates.length; i++) {sum += candidates[i];path.add(candidates[i]);backtracking(candidates, target, sum, i); // 不用 i+1 了，表示可以重复读取当前的数sum -= candidates[i];path.remove(path.size() - 1);
}

剪枝操作：

在进行操作前，先对总组合进行排序，排序之后，如果下一层的sum（也就是本层的sum+candidate[i])>target，就可以结束本层遍历的for循环。那剪枝就需要在for循环的条件上做文章：

// 剪枝优化
class Solution {public List<List<Integer>> combinationSum(int[] candidates, int target) {List<List<Integer>> res = new ArrayList<>(); // 初始化结果列表Arrays.sort(candidates); // 将候选数组排序，以便剪枝和提高搜索效率backtracking(res, new ArrayList<>(), candidates, target, 0, 0); // 调用回溯函数进行组合求和return res; // 返回结果列表}public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {// 如果当前的和等于目标值，将当前路径加入结果列表中，表示找到了一组满足条件的组合if (sum == target) {res.add(new ArrayList<>(path));return;}for (int i = idx; i < candidates.length; i++) {// 如果当前和加上当前候选数超过了目标值，则终止当前循环，因为之后的候选数只会更大if (sum + candidates[i] > target) break;path.add(candidates[i]); // 将当前候选数添加到路径中// 递归调用回溯函数，在新的路径上继续搜索backtracking(res, path, candidates, target, sum + candidates[i], i);path.remove(path.size() - 1); // 回溯，移除路径 path 最后一个元素，以便尝试其他组合}}
}