
🔥个人主页:guoguoqiang. 🔥专栏:数据结构

一、树的基本概念
1.概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因
为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
没有前驱节点的结点叫做根结点
在树中,子树不能有交集,不然就是图。
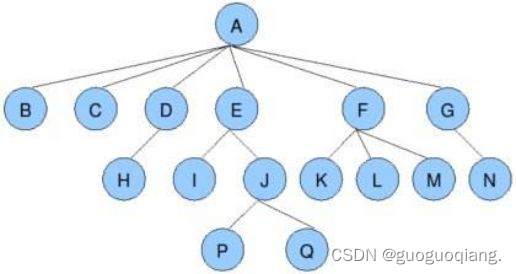
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
2.树的表示
树的表示通常是通过左孩子右兄弟来表示的。
parent=(child-1)/2;
左孩子=2parent+1;
右孩子=2parent+2;
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};

3.树在实际中的应用
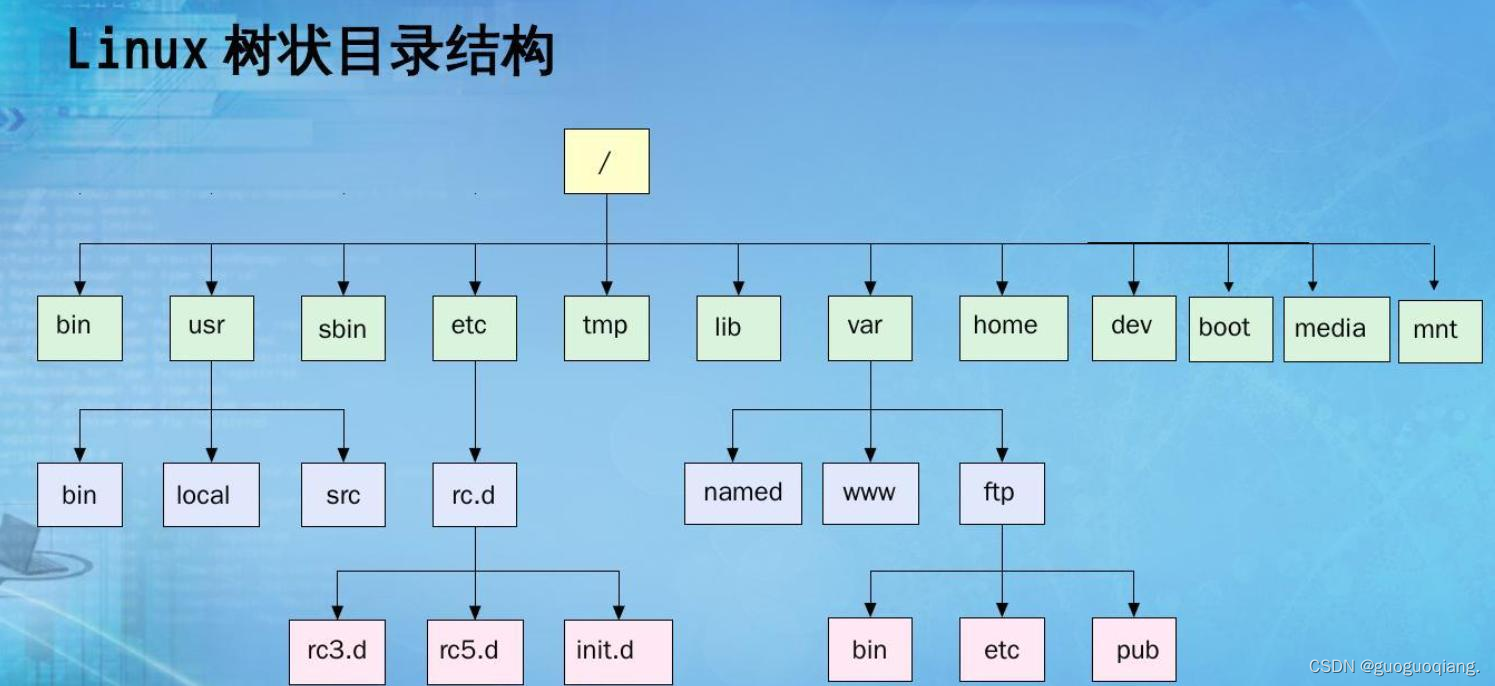
二、二叉树的概念及结构
1.二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
二叉树是有序树 左子树右子树不能颠倒,二叉树的度不能大于2.
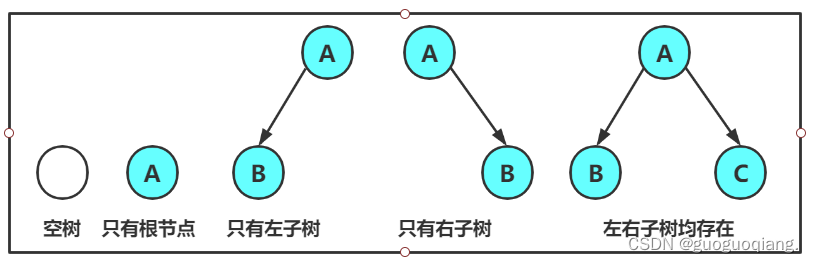
有两种特殊的二叉树:
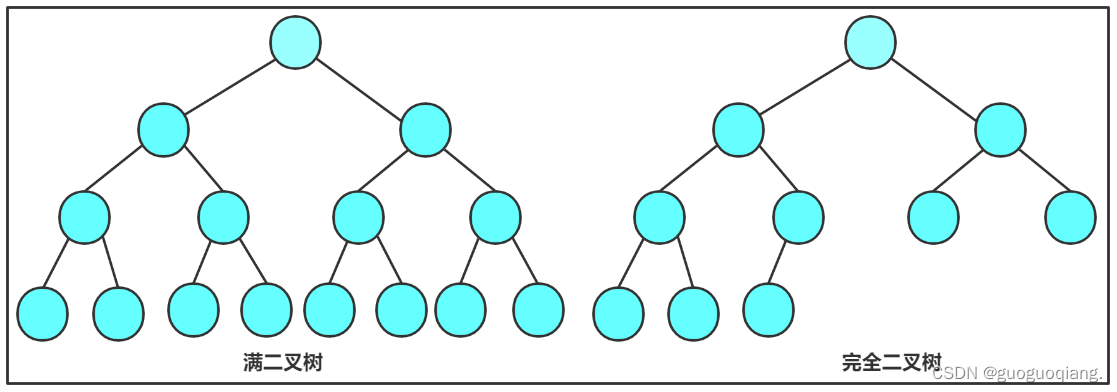
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K
的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对
应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1)个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1 .
- 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为 n2,则有 n0=n2 +1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1) (ps:是log以2为底,n+1为对数)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对
于序号为i的结点有:- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
- 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B)
A 不存在这样的二叉树
B 200
C 198
D 199
2.下列数据结构中,不适合采用顺序存储结构的是(A )
A 非完全二叉树
B 堆
C 队列
D 栈
3.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )//n0+n2=2n n0=n2+1
A n
B n+1
C n-1
D n/2
4.一棵完全二叉树的节点数位为531个,那么这棵树的高度为(B )//log2 512=9;
A 11
B 10
C 8
D 12
5.一个具有767个节点的完全二叉树,其叶子节点个数为(B)//n0+n1+n2=767 2n0-1+n1=767
A 383
B 384
C 385
D 386
3.二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
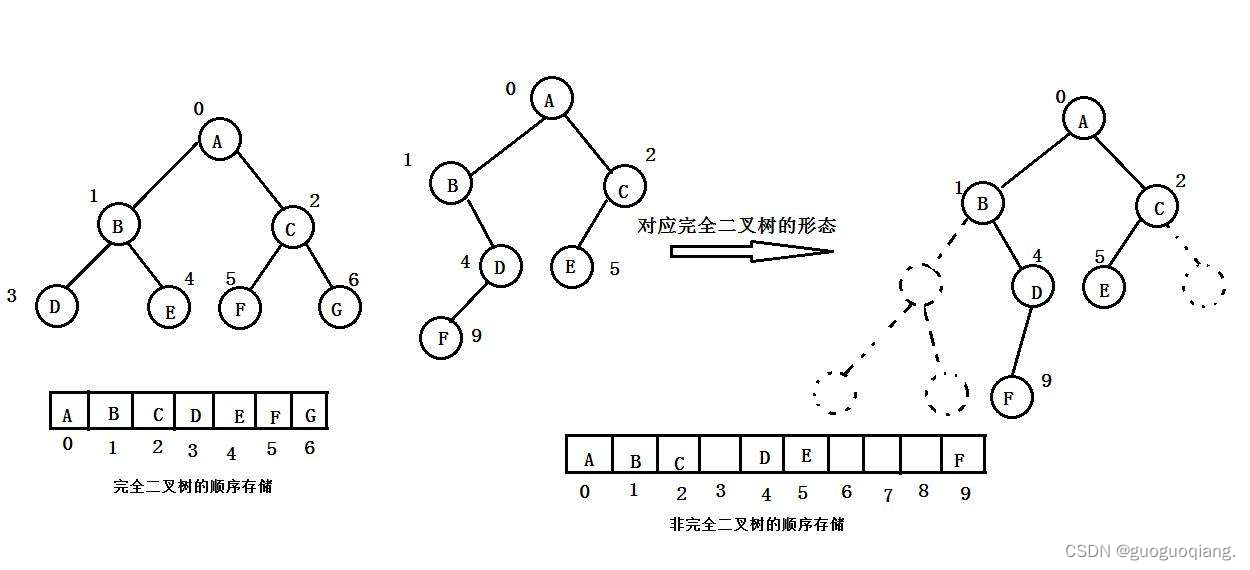
- 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空
间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺
序存储在物理上是一个数组,在逻辑上是一颗二叉树。
parent=(child-1)/2;
左孩子=2parent+1;
右孩子=2parent+2;
通过上述公式构建二叉树。
- 链式存储
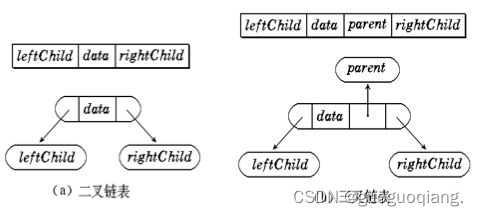
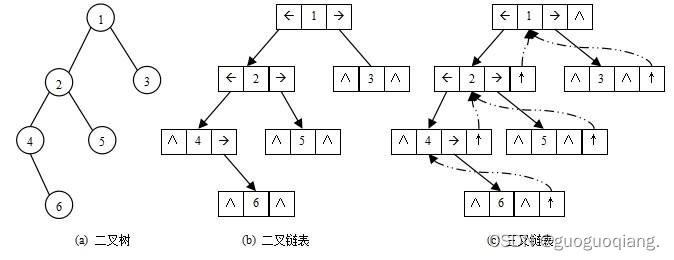
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是
链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。链式结构又分为二叉链和三叉链
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pParent; // 指向当前节点的双亲
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
};
本篇内容到此结束,感谢大家观看!

(二))




)
)
测算)
实践)

_kaic)




)


