操作环境：

MATLAB 2022a

1、算法描述

短时傅里叶变换（Short-Time Fourier Transform，STFT）是傅里叶变换的一种扩展，用于分析信号在时域和频域上的变化。描述如下：

1. **时域与频域分析**：
   - 信号通常以时域的形式表示，即信号随着时间的变化。傅里叶变换可以将信号从时域转换到频域，揭示信号在不同频率上的成分。
2. **窗函数**：
   - STFT 引入了一个称为窗函数的概念。窗函数是一个在时间上截断信号的函数，它允许我们将信号分成小块以进行频域分析。
3. **局部时域分析**：
   - STFT 将信号分成许多小时间段，并在每个时间段上应用傅里叶变换。这使得我们能够在不同时间点上观察信号的频率特性，从而获得信号在时域和频域上的局部信息。
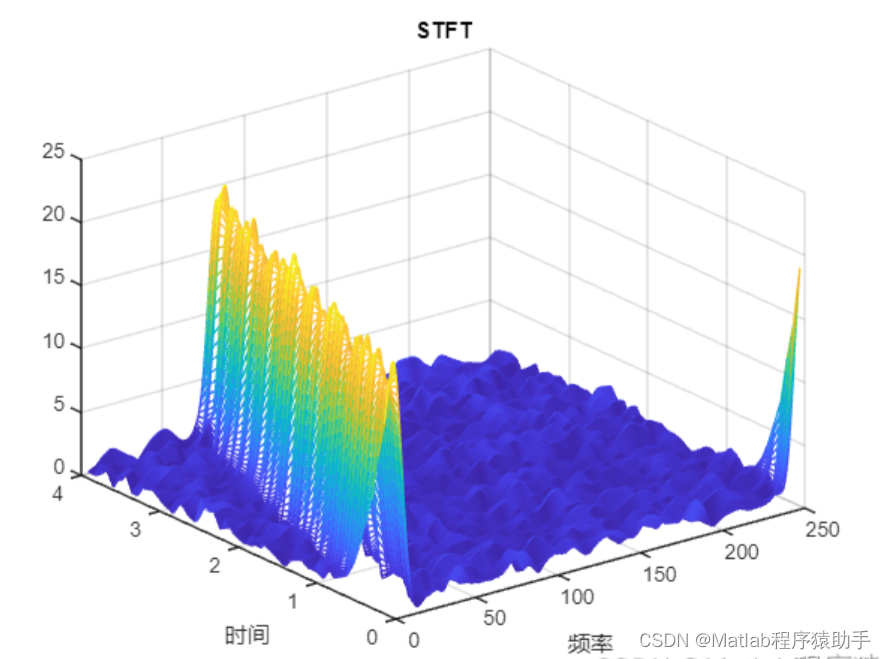
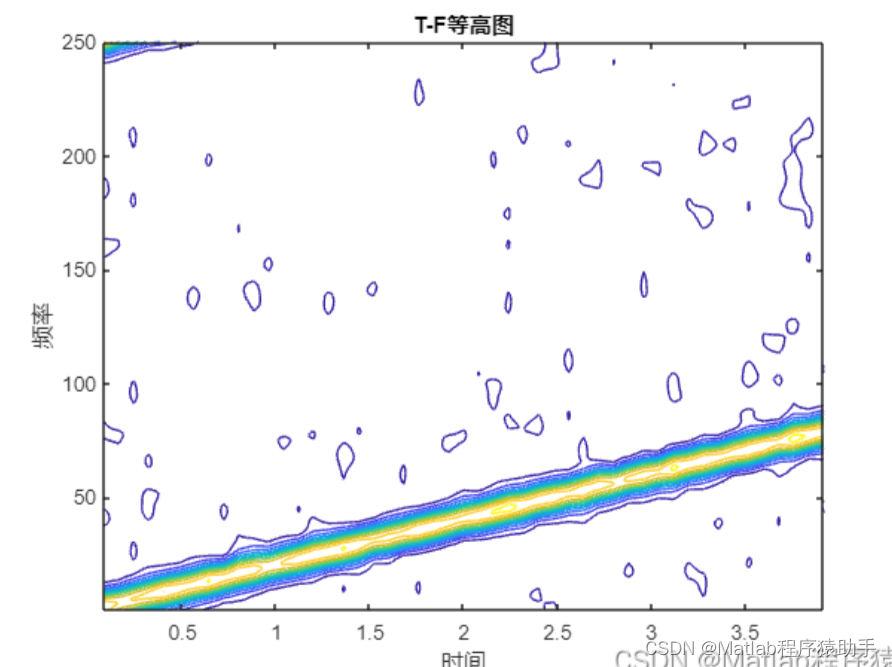
4. **时频图谱**：
   - STFT 的输出是一个称为时频图谱（Spectrogram）的二维数组。在时频图谱中，时间沿水平轴，频率沿垂直轴，颜色表示相应频率成分的强度或能量。
5. **频率分辨率与时间分辨率的权衡**：
   - STFT 的窗口大小（窗口宽度）决定了频率分辨率，而窗口的移动步长决定了时间分辨率。选择合适的窗口大小和移动步长是对频率和时间分辨率进行权衡的关键。
6. **应用**：
   - STFT 在许多领域都有广泛应用，包括信号处理、音频处理、图像处理、通信等。它使我们能够分析具有时变特性的信号，并从中提取出有用的信息。

总的来说，短时傅里叶变换允许我们在时间与频率上同时分析信号，使得我们能够更好地理解信号的特性以及其中包含的信息。

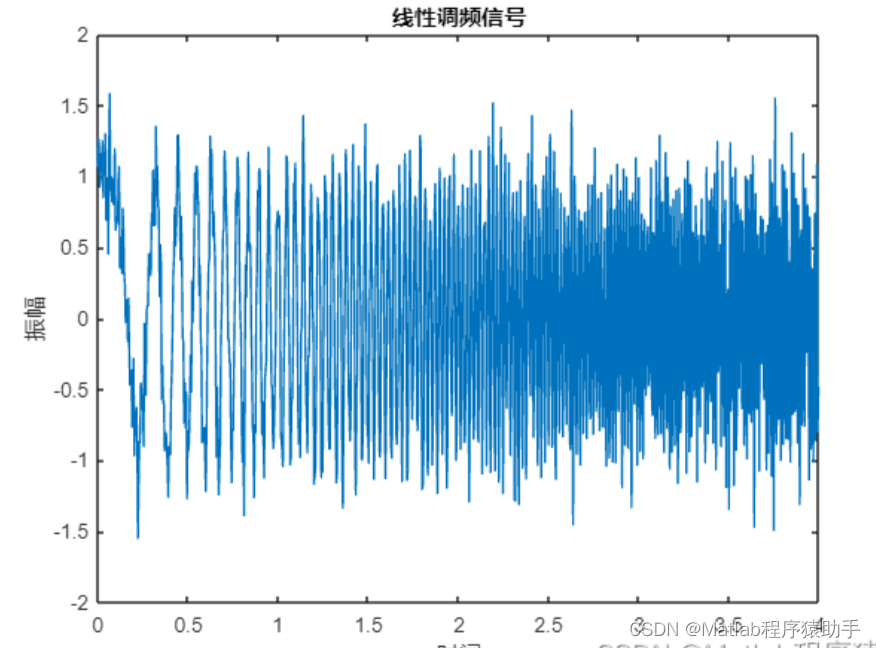
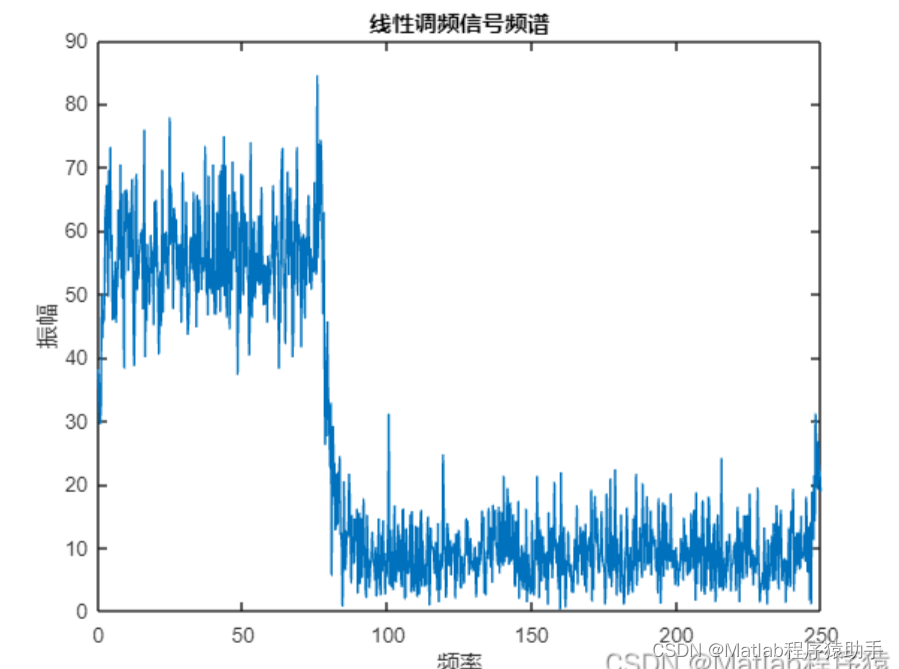
2、仿真结果演示

3、关键代码展示

略

4、MATLAB 源码获取

点击下方原文链接获取

【MATLAB源码-第23期】基于matlab的短时傅里叶STFT信号变换仿真，得到信号的时频曲线图。_短时傅里叶变换画时频图-CSDN博客文章浏览阅读498次。这使得我们能够在不同时间点上观察信号的频率特性，从而获得信号在时域和频域上的局部信息。- STFT 的窗口大小（窗口宽度）决定了频率分辨率，而窗口的移动步长决定了时间分辨率。短时傅里叶变换（Short-Time Fourier Transform，STFT）是傅里叶变换的一种扩展，用于分析信号在时域和频域上的变化。- STFT 在许多领域都有广泛应用，包括信号处理、音频处理、图像处理、通信等。总的来说，短时傅里叶变换允许我们在时间与频率上同时分析信号，使得我们能够更好地理解信号的特性以及其中包含的信息。_短时傅里叶变换画时频图https://blog.csdn.net/Koukesuki/article/details/132801308?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522171189404916800215077547%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=171189404916800215077547&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-132801308-null-null.nonecase&utm_term=23%E6%9C%9F&spm=1018.2226.3001.4450