二叉树|450.删除二叉搜索树中的节点

力扣题目链接

class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root; // 第一种情况：没找到删除的节点，遍历到空节点直接返回了if (root->val == key) {// 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点if (root->left == nullptr && root->right == nullptr) {///! 内存释放delete root;return nullptr;}// 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点else if (root->left == nullptr) {auto retNode = root->right;///! 内存释放delete root;return retNode;}// 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点else if (root->right == nullptr) {auto retNode = root->left;///! 内存释放delete root;return retNode;}// 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点（root）左子树放在cur的左孩子的位置TreeNode* tmp = root;   // 把root节点保存一下，下面来删除root = root->right;     // 返回旧root的右孩子作为新rootdelete tmp;             // 释放节点内存（这里不写也可以，但C++最好手动释放一下吧）return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};

删除节点都要手动释放内存。

这题对我而言代码部分有点难。

代码随想录 (programmercarl.com)

思路

搜索树的节点删除要比节点增加复杂的多，有很多情况需要考虑，做好心理准备。

#递归

递归三部曲：

确定递归函数参数以及返回值

说到递归函数的返回值，在二叉树：搜索树中的插入操作 (opens new window)中通过递归返回值来加入新节点，这里也可以通过递归返回值删除节点。

代码如下：

TreeNode* deleteNode(TreeNode* root, int key)

确定终止条件

遇到空返回，其实这也说明没找到删除的节点，遍历到空节点直接返回了

if (root == nullptr) return root;

确定单层递归的逻辑

这里就把二叉搜索树中删除节点遇到的情况都搞清楚。

有以下五种情况：

第一种情况：没找到删除的节点，遍历到空节点直接返回了
找到删除的节点
- 第二种情况：左右孩子都为空（叶子节点），直接删除节点，返回NULL为根节点
- 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
- 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
- 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

第五种情况有点难以理解，看下面动画：

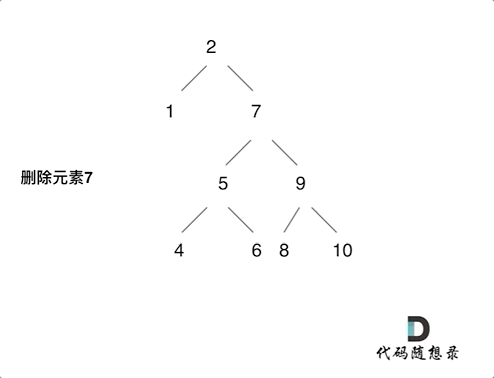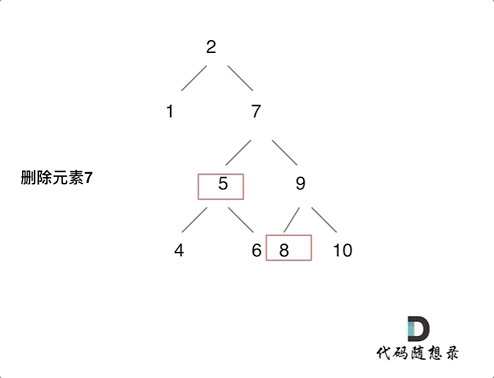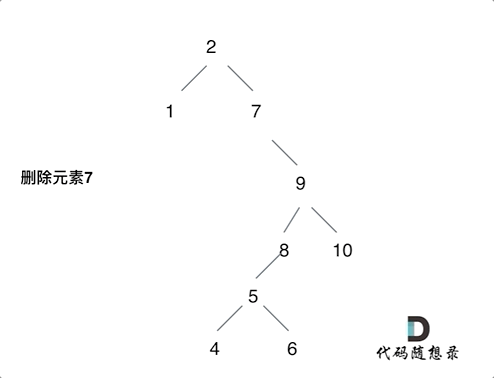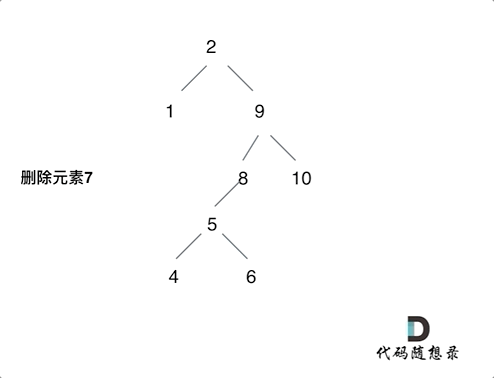
450.删除二叉搜索树中的节点

动画中的二叉搜索树中，删除元素7，那么删除节点（元素7）的左孩子就是5，删除节点（元素7）的右子树的最左面节点是元素8。

将删除节点（元素7）的左孩子放到删除节点（元素7）的右子树的最左面节点（元素8）的左孩子上，就是把5为根节点的子树移到了8的左孩子的位置。

要删除的节点（元素7）的右孩子（元素9）为新的根节点。.

这样就完成删除元素7的逻辑，最好动手画一个图，尝试删除一个节点试试。

代码如下：

if (root->val == key) {// 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点// 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点if (root->left == nullptr) return root->right;// 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点else if (root->right == nullptr) return root->left;// 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点（root）左子树放在cur的左孩子的位置TreeNode* tmp = root;   // 把root节点保存一下，下面来删除root = root->right;     // 返回旧root的右孩子作为新rootdelete tmp;             // 释放节点内存（这里不写也可以，但C++最好手动释放一下吧）return root;}
}

这里相当于把新的节点返回给上一层，上一层就要用 root->left 或者 root->right接住，代码如下：

if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;

整体代码如下：（注释中：情况1，2，3，4，5和上面分析严格对应）

class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root; // 第一种情况：没找到删除的节点，遍历到空节点直接返回了if (root->val == key) {// 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点if (root->left == nullptr && root->right == nullptr) {///! 内存释放delete root;return nullptr;}// 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点else if (root->left == nullptr) {auto retNode = root->right;///! 内存释放delete root;return retNode;}// 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点else if (root->right == nullptr) {auto retNode = root->left;///! 内存释放delete root;return retNode;}// 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点（root）左子树放在cur的左孩子的位置TreeNode* tmp = root;   // 把root节点保存一下，下面来删除root = root->right;     // 返回旧root的右孩子作为新rootdelete tmp;             // 释放节点内存（这里不写也可以，但C++最好手动释放一下吧）return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};