Abstract

   影响力最大化（IM）被表述为从社交网络中选择一组初始用户，以最大化受影响用户的预期数量。研究人员在设计各种传统方法方面取得了巨大进展，其理论设计和性能增益已接近极限。在过去的几年里，基于学习的IM方法的出现，对未知图实现了比传统方法更强的泛化能力。然而，基于学习的IM方法的发展仍然受到根本性障碍的限制，包括1）有效求解目标函数的困难； 2）难以描述多样化的潜在扩散模式； 3) 在各种节点中心性约束的 IM 变体下调整解决方案的难度。为了应对上述挑战，我们设计了一个新颖的框架 DeepIM 来生成地表征种子集的潜在表示，并提出以数据驱动和端到端的方式学习多样化的信息传播模式。最后，我们设计了一种新颖的目标函数，以在灵活的基于节点中心性的预算约束下推断最佳种子集。对合成数据集和真实数据集进行了广泛的分析，以展示 DeepIM 的整体性能。代码和数据可在以下网址获取：https://github.com/triplej0079/DeepIM。

1. Introduction

   作为网络分析的基础研究问题之一，影响力最大化（IM）的目标是找到一组种子节点，使社交网络中的影响力传播最大化。 IM由于其巨大的商业价值，近年来得到了广泛的研究。例如，考虑用于推广商业产品的病毒式营销（Chen et al., 2010）的情况，公司可能希望从一些最初选择的用户中传播新产品的采用，所选择的初始用户预计会传播他们各自的社交网络上有关产品的信息。这种级联过程将持续下去，最终，很大一部分用户将尝试该产品。除了病毒式营销之外，IM 也是许多其他关键应用的基石，例如网络监控（Wang 等人，2017）、错误信息遏制（Yang 等人，2020）和好友推荐（Ye 等人，2012）。

   作为典型的组合优化问题，由于信息扩散的随机性和问题的难度，检索（接近）最优种子集以最大化网络中的影响力具有挑战性。传统的（非基于学习的）IM 方法（Leskovec 等人，2007；Kempe 等人，2003；Tang 等人，2014；2015；Nguyen 等人，2016；Saito 等人，2012）在过去的十年中取得了巨大的进步，Li 等人。 （2019b）甚至在特定扩散模型下获得了精确的解决方案。传统方法的共性是明确要求信息扩散模型作为模型输入。然而，现实世界的信息扩散过程是复杂的，不能用规定的扩散模型简单地建模。随着机器/深度学习的最新发展，很自然地考虑采用基于学习的方法来表征底层扩散过程。

    尽管该领域已经取得了很大的进展，但目前基于学习的IM解决方案的研究仍处于起步阶段，存在以下基本障碍。1 )。高效优化目标函数的难点。基于学习的IM方法倾向于利用深度网络表示(张杰等, 2022 ; Kumar et al , 2022)和深度强化学习来解决连续空间中的离散问题( Tian et al .，2020 )；李等人，2022）。尽管它们可以通过传统方法获得具有竞争力的性能，但它们的可扩展性和执行效率存在问题，因为（a）需要在每个操作中迭代更新所有节点嵌入以及（b）计算影响力传播的#P-hardness（林等人，2017）。 2）。自动识别和建模实际扩散过程的困难。为了最大化网络中的影响力传播，底层的信息传播模式是必不可少的部分，因为它决定了整体信息传播的结果。然而，如果没有启发式方法，传统方法和基于学习的方法都无法表征潜在的扩散过程。为了解决这个问题，传统和当前基于学习的方法都利用预定义的扩散模型（例如线性阈值（LT）和独立级联（IC））作为输入来解决组合优化问题。

   尽管它们仅适用于遵循启发式的过程，但现实世界的网络过程比启发式复杂得多，并且很大程度上是未知的。 3）。适应各种节点中心性约束的 IM 问题的解决方案的难度。 IM 有很多与节点中心性相关的变体，例如种子节点数量的约束、种子节点总度的约束等。当前基于学习的 IM 解决方案没有明确定义解决不同节点中心性约束的 IM 问题的范式，这对其解决方案的适应性提出了另一个挑战。

   为了解决上述挑战，我们提出了一种新颖的框架 - DeepIM，通过开发一种将初始离散优化域嵌入到更大的连续空间中的新颖策略来解决 IM 问题。值得注意的是，我们建议通过保留种子集的表达性并直接在连续空间中进行优化来学习种子集的潜在表示，以降低问题的难度。我们进一步设计了一个基于学习的扩散模型，以端到端的方式表征潜在的扩散动态。此外，我们开发了一个通用的种子集推理框架，可以在统一的预算约束下直接优化和生成集合嵌入。最后，我们总结我们的贡献如下：

• 问题。

我们将基于学习的 IM 问题表述为将初始离散优化域嵌入到连续空间中以简化优化，并确定其在实际应用中产生的独特挑战。

• 框架。

我们建议对潜在空间中种子集的表示进行建模，并且该表示与以端到端方式学习底层图扩散过程的模型联合训练。

• 适应性。

我们提出了一种新颖的约束优化目标函数，通过利用深度图嵌入来推断最佳种子集，该函数可以在任意节点中心性相关约束下应用。

• 评估。

我们对四个真实世界数据集进行了广泛的实验，以证明所提出方法的性能。与各种应用场景中的其他最新技术相比，DeepIM 在寻找种子集以最大化影响力方面取得了最佳效果。

2. Related Work

 2.1. Learning-based Influence Maximization

    影响力最大化（IM）首先由 Kempe 等人将其表述为组合优化问题。 （2003），它激发了未来十年的广泛研究和应用。大多数传统（即非基于学习的）IM 方法可以分为基于模拟、基于代理和启发式。传统方法在特定扩散模型下高效地获得了近似或精确的解。请注意，杜等人。 （2014）；瓦斯瓦尼等人。 （2017）提到了从级联数据中学习影响的可能性；然而，他们仍然假设规定的模型指导扩散模式，特别是覆盖函数。我们建议读者参阅最近的调查（Li et al., 2018；Banerjee et al., 2020），以获取对传统方法的更详细的评论。

  基于学习的方法利用深度学习来解决传统IM方法缺乏泛化能力的缺点。开创性的工作（Lin et al., 2015; Ali et al., 2018）首先将强化学习与 IM 相结合，并引发了利用深度强化学习来解决 IM 问题的广泛工作。现有的最先进的解决方案（Li et al., 2019a; Tian et al., 2020; Manchanda et al., 2020; Li et al., 2022; Chen et al., 2022）遵循类似的范式：学习节点或网络的潜在嵌入，并将当前节点嵌入作为代理的状态，以选择下一个种子节点作为动作，其中奖励是其边际影响增益。除了基于强化学习的 IM 方法之外，还存在仅利用图神经网络将社会影响编码为节点嵌入和引导的方法（Kumar et al., 2022; Kamarthi et al., 2019; Panagopoulos et al., 2020）节点选择过程。当前基于学习的IM方法的症结也很明显，基于学习的IM方法的模型复杂性和适应性仍然无法与传统方法相比。特别是，当前基于机器学习的算法既不能处理多样化的扩散模式，也不能保证解决方案的质量和模型的可扩展性。

2.2. Graph Neural Network

  图神经网络（GNN）（Wu et al., 2020）是一类深度学习方法，旨在对图描述的数据进行推理。 GNN 的一般范式在节点特征变换之间交替以及邻居节点的信息聚合。对于 Klayer GNN，节点聚合 K 跳邻居内的信息。具体来说，第k层变换为：

其中ak是聚合特征，hk是第k层节点特征。聚合函数 A(·) 和组合函数 C(·) 函数的灵活性导致了不同的 GNN 模型（Veliˇ ckovi ́ c et al., 2017; Kipf & Welling, 2016; Xu et al., 2018; Wang et al., 2022b）。节点或图的高级表示用于不同的任务。 GNN 已应用于各种学习任务，例如信息扩散估计（Chamberlain 等人，2021；Xia 等人，2021；Ko 等人，2020）、图源定位（Wang 等人，2022a；Ling 等人） ., 2022b)、深度图生成 (Ling et al., 2021; 2023a;b) 和图类比推理 (Ling et al., 2022a)。在这项工作中，我们利用 GNN 来表征底层的扩散模式，并构建一个端到端模型来估计影响.

3. Problem Formulation

   给定图 G = {V, E}，IM 问题旨在通过选择最优种子节点集 x ⊆ V 来最大化 G 中受影响的节点数量。特别地，IM的评估依赖于由θ参数化的影响扩散模型：y=M(x,G;θ)，其中如果M(·)是独立的级联模型，则θ可以是每个节点上的感染概率的集合，或者如果 M (·) 是基于 GNN 的，则聚合/组合函数中的参数集。我们表示 x ∈ {0, 1}|V |作为源节点集的向量表示，其中第 i 个元素 xi = 1，如果 vi ∈ x，则 xi ∈ x，否则 xi = 0。输出 y ∈ R+ 测量受感染节点的总数（Li et al., 2018）。基于影响力传播的形式化，IM问题定义如下：

定义 1（影响力最大化）

通用 IM 问题需要从 V 中选择一组 k 个用户作为种子集，以最大化影响力传播：

其中 ̃ x 是能够在 G 中产生最大影响力传播的最优种子节点集。

 直观上，选择 ̃ x 在很大程度上取决于底层的扩散过程。我们已经见证了许多使用 GNN 和强化学习开发算法来解决该问题的工作。然而，由于以下挑战，现有基于学习的 IM 框架的表达能力和泛化能力仍然受到限制。

Challenges

   首先，大多数现有的基于学习的 IM 框架都会计算潜在节点嵌入，以选择高影响力的节点。然而，它们的目标函数需要在每个操作/优化步骤迭代更新每个节点的潜在嵌入，无论它们是否包含在当前 x 中。如果我们处理百万规模的网络，这会带来严重的可扩展性问题。其次，即使我们利用深度节点/网络嵌入和各种奖励函数来指导节点选择过程，现有框架仍然是针对特定扩散模型量身定制的（例如，它们将 M (·) 建模为显式 IC 和 LT 模型）。然而，这些简单的扩散模型无法满足实际应用的需求。此外，为了减轻#P-hard影响估计的计算开销，基于学习的IM方法依赖于传统方法的技术，例如基于代理和基于采样的估计方式，这使得可扩展性和泛化性更差。最后，存在大量受节点中心性约束的 IM 变体。例如，除了调节种子节点的预算外，我们可能还需要调节选择种子节点的总成本。基于学习的IM解决方案根据不同的应用场景设计了不同的目标函数，并且对于所有与节点中心性相关的约束没有明确定义的方案。

4. DeepIM

   在本节中，我们提出 DeepIM 框架来减轻基于学习的 IM 方法的计算开销并自动识别底层的扩散模式。该框架可分为两个阶段：学习阶段用于表征观察到的种子集的概率并对底层信息传播分布进行建模，推理阶段用于优化连续空间中种子的选择以最大化影响力传播。

4.1. Learning Representation of Seed Set

  为了构建有效且高效的目标函数，我们建议在给定图 G 的情况下表征种子节点集 p(x) 在 x 上的概率，因为学习 p(x) 可以帮助描述种子集的基本性质。然而，学习这种概率并不是一项简单的任务，因为不同的节点在每个种子集中是相互连接的，并且基于 G 的拓扑结构高度相关。这些连接使得节点之间的关系非常复杂，并且比其他类似的组合问题更难以破译。

Learning Probability over Seed Nodes

  我们没有直接对高度棘手的概率 p(x) 进行建模，而是引入一个未观察到的潜在变量 z 来表示 x 并定义条件分布 p(x|z) 来量化可能性。这些潜在变量的维度比观察到的次优种子集低得多，这可以产生压缩表示。特别是，我们边缘化潜在变量以获得 p(x) =∫ p(x, z) dz = ∫ p(x|z)p(z) dz。后验似然 p(z|x) = p(x|z) · p(z)/p(x) 允许我们在给定观察到的种子集 x 的情况下推断 z。在这项工作中，我们采用自动编码器来生成推断后验，其中编码器 fφ（由 φ 参数化）和解码器 fψ（由 ψ 参数化）分别用于表征后验分布和条件分布的可能性。自动编码器的目标是最大化联合似然：

  

Learning the End-to-end Diffusion Model

   一旦我们了解了种子节点 p(x) 的潜在分布，下一步就是更新种子节点集 x 以增加影响力传播的边际增益。当前基于学习的 IM 解决方案仍然假设影响力传播（即 M (x, G; θ)）的计算依赖于规定的数学模型。然而，现实世界的信息扩散是复杂的，在实践中确定最合适的扩散模型并不容易。与现实世界的数据相比，所选的扩散模型可能会被错误指定，并导致较大的模型偏差。此外，扩散网络结构也可以对我们隐藏，因此我们不仅需要学习扩散模型中的参数，还需要学习扩散网络结构（Du et al., 2014）。

  在这项工作中，我们设计了一个基于 GNN 的扩散模型 M (·)，在考虑整体图拓扑的情况下对 x 和 y 之间的关系进行精确建模。基于 GNN 的扩散函数 M (·) 的输出由两个函数组成 M = gr ◦ gu(x, G; θ): 1) τ = gu(x, G; θ)，其中 gu(·) 是基于 GNN 的聚合函数和 τ ∈ [0, 1]|V |是聚合多跳邻域信息后的中间输出。 τ 表示每个节点的感染概率； 2) y = gr(τ ; xi), y ∈ R+ 表示最终的信息传播，其中 gr(·) 是归一化函数（例如 l-1 范数）， xi 是将概率转换为离散值的阈值。基于 GNN 的 M (·) 可视化如图 1 (a) 所示

Definition 2 (Score Monotonicity and Infection Monotonicity).

  给定一个基于 GNN 的扩散模型 M (·) : 2|V | → R+ 和任何两个子集 S, T ⊆ V , M (·) 是分数单调的，如果 xS xT （即 S ⊆ T ）意味着 M (xS, G; θ) ≤ M (xT , G; θ)，其中 xS, xT ∈ {0, 1}|V |分别是种子集 S 和 T 的向量表示。如果 xS xT （即 S ⊆ T ）蕴含 τS τT ，则 M (·) 是单调感染，其中 τS, τT ∈ [0, 1]|V |分别表示种子集 S 和 T 的感染概率。

     单调性是我们在建模整体扩散网络结构时的自然属性。单调扩散模型表明影响力的传播将继续增加。直观上，如果我们选择较大的社区 x′ 作为种子集，则较大的 x′ 本质上会比较小的种子集 x x x′ 感染整个网络中的节点。确保两种单调性的属性使我们能够更好地表征底层的扩散网络结构并模仿现实世界的扩散模式（Dolhansky＆Bilmes，2016）。因此，我们添加约束，使基于 GNN 的扩散模型 M (x, G; θ) 在影响扩散估计过程中保持单调。

Theorem 1 (Monotonicity of GNN Models).

  对于任何基于 GNN 的 M (x, G; θ) = gr ◦ gu(x, G; θ)，其中 gu(x, G; θ) 由方程 1 表示。 (1) 如果 Ak 和 Ck (k ∈ [1, K]) 在方程 (1) 中是非递减的，则 M 是分数和感染单调。 (1) 且 gr 也不减。

  我们进一步说明，在我们在定理 1 中声明的约束下，著名的图注意力网络（GAT）可以是评分和感染单调的。请注意，我们遵循原论文中介绍的 GAT 的标准网络结构。

Corollary 2 (Montonicity of GAT).

  当 gu 是 GAT 时，如果等式中 θk ≥ 0，M 是分数和感染单调。 (1) 且 gr 也不减。

由于篇幅限制，定理1和推论2的证明在附录A中给出。根据定理1和推论2，基于GNN的M(x,G;θ)具有保持单调性的理论保证，并且学习基于 GNN 的 M (x, G; θ) 的目标是在约束下最大化以下概率：

扩散估计效率的知识蒸馏

   我们学习了种子节点的深度表示和具有单调性保证的端到端扩散模型。然而，我们凭经验发现影响力传播 M (x, G; θ) 的计算涉及三个步骤：1）从学习到的后验 p(x|z) 解码节点向量 x； 2）在图G下执行基于GNN的扩散模型M（x，G；θ）； 3) 将 M (x, G; θ) 的概率输出 τ 标准化为实际影响力分布 y。尽管预测结果是准确的，但在处理百万规模的网络时，计算开销仍然是一个负担。受最近知识蒸馏研究的启发，我们建议利用由 M (x, G; θ) 监督的小型但功能强大的学生模型来提高效率。具体来说，学生模型Ms(z; λ)是一个由λ参数化的轻量级神经网络，它直接将从学习的p(z)中采样的潜在变量z作为输入。 Ms(z; λ) 直接返回估计的影响力分布 ys 作为输出。 y = M (x, G; θ)（教师模型）和 ys = Ms(z; λ) 之间的蒸馏损失可以简单为 ‖y − ys‖22

End-to-end Learning Objective.

   最后，为了连接表示学习和扩散模型的学习，我们通过将等式（1）放在一起，以端到端的方式提出了一个统一的目标函数。 （3）和（4）为：

    然而，优化联合概率的期望在计算上可能很困难。相反，我们推导了方程的负对数项。 (5)并根据Jensen不等式推导出其下界作为最终学习目标：

  

  

图 1.DeepIM 由两部分组成。 a）我们利用自动编码器来学习种子节点集的潜在分布并将其压缩为较低维度的 p(z)。然后利用较低维度的 p(z) 来学习端到端的单调扩散模型 M (x, G; θ)，以准确预测扩散。此外，我们采用知识蒸馏模块来训练轻量级学生模型，以保持预测影响力传播的效率。 b) 种子集推断方案通过更新最初从学习的 p(z) 中采样的潜在变量 z 来迭代优化所提出的目标函数，以最大化影响范围。

总体目标包括最小化以重构 x 作为输入的 y 预测的经验误差 − log[pθ(y|x, G)] 以及最小化重构误差。此外，我们最小化蒸馏损失 - log[pλ(ys|z)] 以在整个训练过程中训练学生模型。训练端到端扩散模型和学习种子集分布的自动编码器的总体框架如图 1（a）所示。

4.2. Seed Node Set Inference

   为了推断测试域中高影响力的种子节点集，我们联合利用种子节点集的潜在分布 p(x) 和端到端扩散模型 M (·) 。 （6）。首先，如果自动编码器经过良好的训练并且可以保持连续性（即，潜在空间中的两个接近点一旦解码后不应给出两个完全不同的内容）和完整性（即，对于选定的分布，从潜在空间中采样的点）一旦解码应该给出“有意义的”内容），方程中的自动编码器。 (3) 可以通过利用从所有训练样本中学习到的潜在特征空间 p(z) 来生成内容，即 p(x)。因此，我们建议在低维且噪声较小的潜在空间 p(z) 中交替搜索最优种子节点集 ̃ x。以下推论表明，如果自动编码器同​​时保持连续性和完整性，则相当于使用潜在变量 z 而不是高维 x 来估计影响扩散。

Corollary 3 (Influence Estimation Consistency).

 对于任何 M (fψ(z(i)), G; θ) > M (fψ(z(j)), G; θ)，我们有 M (x(i), G; θ) > M (x( j)，G；θ)。

推论3的证明可以在附录中找到。根据推论，我们可以通过在以下联合概率中优化 z 来找到能够产生最大影响的最优种子集：maxz E[pθ(y|x, G) · pψ(x|z)]。

适应具有节点中心性约束的不同 IM 变体。自从 IM 被引入（Kempe et al., 2003）以来，近年来人们在节点上的各种预算约束设置下研究了 IM。为了增强 DeepIM 的适应性，我们设计了一个统一的约束，允许在各个节点上的不同预算下推断种子集。具体来说，目标 Lpred 给出为：

 其中 Σ|V | i=0 F (vi, G) · xi 是应用于各个节点的广义预算约束，k 是实际预算。对于仅需要选择给定数量种子节点的普通 IM 问题， Σ|V | i=0 F (vi, G) · xi 可以导出为 ‖x · 1‖1，其中 1 ∈ {1}N×1 是全 1 向量，表示选择每个节点的价格相同。此外，对于节点度受限的 IM 问题 (Leskovec et al., 2007; Nguyen et al., 2017)， i=0 F (vi, G) · xi 可推导为 ‖x · A‖1，其中 A ∈ {0, 1}N×N 为网络 G 的邻接矩阵，且 ‖x · Ai‖1 ≤ k代表总种子节点度的 l1-范数受预算 k 限制。预算约束 F(vi, G) · xi ≤ k 也可以很容易地设计、组合和调整，以解决每个节点上价格不一致的 IM 变体。通过提出的灵活约束，可以部分解决 IM 方法适应性的挑战。

种子集推理的实现细节

  我们在图 1 (b) 中可视化了我们的推理过程。具体来说，推理框架首先从学习到的潜在分布 p(z) 中采样潜在变量 z。根据推理目标函数 Eq 迭代优化潜在变量 z。 （7）获得较大的边际收益（影响力扩散）。请注意，基于学习的扩散模型 pθ(y|x, G) 可以在学生扩散模型 Ms(z; λ) 和基于 GNN 的扩散模型 M (x, G; θ) 之间切换，以实现效率或功效。此外，约束目标函数 Eq. （7）式无法直接计算，因此我们提供了一个实用版本的推理目标函数：由于扩散观测值 y 符合高斯分布，而种子集 x 符合伯努利分布，因此我们可以简化式（7）。 (7) 作为

  其中 ̃ y 给出为最佳影响力分布（即 ̃ y = |V |），附录中提供了上述方程的完整推导。此外，我们利用投影梯度下降并提出正则化函数 Φ(x)，以根据不同的约束将预测的种子集 x 保持在有效区域内。例如，Φ(x)可以定义为当选择每个节点的价格相等时，选择具有最高概率的k个节点。 （7）。 Φ(x) 也可以定义为从 x/c(x) 中经济高效地选择前 k 个节点，其中 c(x) 表示一个节点上的预算（例如，节点度）。最后，算法 1 总结了优化过程。具体来说，我们首先在第 1 行采样初始潜在变量 z。从第 2 - 6 行，我们迭代解决方程 1 中提出的优化问题。 (7) 通过梯度下降优化器（例如，Adam)，同时用 Φ(·) 规范有效区域中的预测种子集。图1（b）说明了推理目标学习的整体过程。我们提供了两个方程的推导细节。附录A中的（6）和（8）。

5. Experiment

  在本节中，我们比较了我们提出的 DeepIM 框架在六个真实网络中在各种设置下最大化影响力的性能，并通过案例研究定性地展示了 DeepIM 的性能。由于篇幅限制，更多详细的实验设置、超参数设置、数据集描述和比较方法可以在附录中找到。

5.1. Experiment Setup

  我们的主要目的是评估方程式中定义的预期影响力传播。 (2)各种IM应用场景下。由于 DeepIM 可以轻松适应不同的扩散模式，因此我们选择了 IM 问题中常用的两个代表性模型，即 LT 模型和 IC 模型。此外，我们还评估了易感者-感染者-易感者（SIS）流行病模型（Kermack＆McKendrick，1927）下的IM问题，其中主要区别是激活的节点可以在SIS中停用。由于篇幅限制，非渐进扩散模型的实验见附录。

数据。所提出的 DeepIM 与六个真实世界数据集上的其他方法进行了比较，包括 Cora-ML、Network Science、Power Grid、Jazz、Digg 和 Weibo。我们还采用了一个合成数据集，它是由 Erdos-Renyi 算法生成的具有 50, 000 个节点的随机图（Erd ̋ os 等人，1960）。

数据统计如表1所示。我们随机采样种子节点集x，种子大小与|V|成正比。每个网络的。然后我们使用 IC、LT 和 SIS 模型来计算最终的影响力分布 y。然后 {(x, y)} 集作为我们算法的训练集。

5.2. Comparison Method.

  除了比较基于 GNN 的扩散模型 M(x, G; θ)（表示为 DeepIM）和学生扩散模型 Ms(z; λ)（表示为 DeepIMs）之间的模型性能外，我们还采用了四组比较方法，所有这些方法概述如下。传统 IM：1) IMM (Tang et al., 2015)、2) OPIM-​​C (Tang et al., 2018) 和 3) SubSIM (Guo et al., 2020)。基于学习的 IM：1) IMINFECTOR (Panagopoulos et al., 2020)、2) PIANO (Li et al., 2022) 和 3) ToupleGDD (Chen et al., 2022)。在线 IM：OIM（Lei 等，2015）。预算约束 IM：CELF（Leskovec 等，2007）。此外，我们还比较了学生模型 DeepIMs（即与简化扩散模型 Ms(·) 相结合）的性能。

5.3. Quantitative Analysis

  我们评估了 DeepIM 在各种 IM 应用方案下最大化对其他方法的影响的性能。每个模型在每个数据集中选择1%、5%、10%和20%的节点作为种子节点，我们让每个扩散模型进行模拟，直到扩散过程停止并记录100轮的平均影响力扩散。我们报告最终受感染节点的百分比（即受感染节点数/节点总数）。

IM under IC Model

  我们首先在 IC 扩散模式下检查 DeepIM 相对于其他基线方法的有效性。

表 2. IC 扩散模式下的性能比较。 − 表示内存不足错误。 （“最佳”以粗体突出显示。）

如表 2 所示，DeepIM 在所有数据集上都能取得比其他方法更好的整体性能。与传统方法相比，IMM、OPIM 和 SubSIM 是基于保留集采样和各种近似技术的三种最先进的方法，它们在所有数据集上生成相似的结果；然而，它们依靠不同的启发式方法来指导节点选择以提高效率，并且无法解码种子集的底层分布。 OIM 在大多数数据集中比传统方法取得了更好的性能，因为它可以自动迭代更新边权重。但OIM的缺点也很明显：它是针对特定的IC扩散模型量身定制的，在现实场景中适用性较差。最后，基于学习的 IM 方法（IMINFECTOR、PIANO 和 ToupleGDD）由于其更大的模型尺寸和更好的泛化能力，与传统方法相比，取得了有竞争力的、普遍更好的性能。然而，利用强化学习的基于学习的方法存在可扩展性问题，并且无法应用于数十亿规模的网络（例如 Digg 和微博），这使得它们很难应用于现实场景。与基于学习的方法相比，DeepIM提出了一种更鲁棒的方法来学习端到端扩散模型并直接在潜在空间中搜索高影响力的节点集，可以更好地捕获底层扩散动态并解决可扩展性问题。此外，DeepIMs 还集成了轻量级端到端与其他基于学习的方法相比，基于学习的扩散模型可以保留功效和效率。

LT 模型下的 IM。

然后，我们假设 LT 作为扩散模型，评估相对于初始种子集大小的最终影响扩散。

表 3. LT 扩散模式下的性能比较。 − 表示内存不足错误。 （“最佳”以粗体突出显示）

如表 3 所示，DeepIM 可以生成更优质的种子集来感染最多数量的节点，并在所有数据集上明显优于其他方法。值得注意的是，DeepIM 在综合数据集中展现了其优越性，选择 20% 的节点作为初始种子集时，可以有效地将影响传播到整个网络，而其他方法最多只能感染网络的 70% 节点。具体而言，DeepIM 和 DeepIM 在 Jazz 数据集中优于其他方法，平均优于其他方法 200%，在 Synthetic 数据集中优于其他方法 30%。究其原因，很大程度上是由于其他方法在各种扩散模型下缺乏泛化能力。

IM with Budget Constraint

  然后我们将 IC 和 LT 模型下 DeepIM 和 CELF 生成的种子集的质量与预算约束进行比较，本文将这样的预算明确定义为节点度。

图 2. y 轴在预算约束下随节点规模增长（x 轴：1%、5%、10% 和 20%）的影响力传播（受感染节点总数）。图2a-2e和图2f-2j分别在IC和LT模型下进行评估。

从图 2 中可以看出，我们提出的方法在所有不同规模的网络中通常都比 CELF 表现得更好，并且在 LT 模型下（图 2f - 2j），边缘更加明显。此外，与 CELF 相比，DeepIM 中影响力传播的增长在所有数据集中的波动较小，这也证明了 DeepIM 的稳定性，因为它能够在考虑预算约束的情况下识别潜在分布种子集。

5.4. Scalability Analysis

  我们记录了与其他基于学习的 IM 解决方案相比，节点大小增加的种子集推理的运行时间。

表 4. 随着节点大小和平均训练时间的增加，平均推理运行时间（以秒为单位）。我们选择 10% 的节点作为种子。

从表 4 中可以清楚地看出，随着图大小的增加，DeepIM 的运行时间呈现近线性增长。此外，与其他基于学习的方法相比，它的推理时间普遍较短（推理时间比第二快的 IMINFECTOR 平均快 20%）。此外，我们的 DeepIM 与轻量级端到端扩散模型相结合，可以大大降低估计预期影响扩散的计算成本，并且比我们的 DeepIM 模型平均推理时间提高了 90%。

5.5. Case Study: Graph Diffusion Visualization

  最后，我们通过案例来展示选取的20%种子节点的分布以及所有节点最终的感染状态，

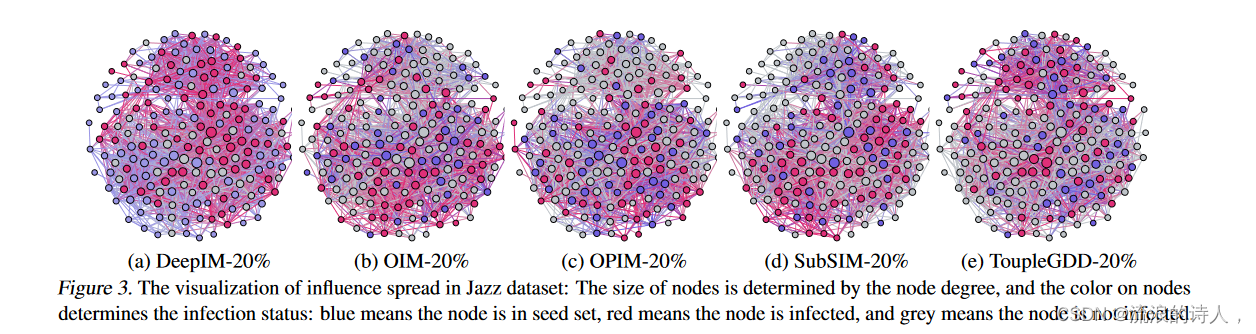图 3 Jazz 数据集中影响力传播可视化：节点大小由节点度决定，节点颜色决定感染状态：蓝色表示节点处于种子集中，红色表示节点被感染，灰色表示该节点未被感染。

如图3所示，其中蓝色节点表示初始种子节点，红色节点表示影响期间被感染的节点传播，灰色节点代表未感染节点。由于易于表示，我们仅可视化 Jazz 数据集的结果，因为它的整体图形尺寸较小。总体而言，DeepIM 在影响力传播方面表现出了更好的表现。由于篇幅限制，我们在附录中比较了不同初始种子集大小（即 10% 和 20%）之间的影响力扩散结果，并在附录中提供了更多讨论。

6. Conclusion

  在本文中，我们提出了一种新的框架，以比现有的基于学习的 IM 方法更稳健和更通用的方式解决 IM 问题。特别是，为了表征种子集的复杂性，我们提出表征种子集的概率并直接在连续空间中搜索更最优的种子集。此外，为了解决底层扩散模式建模的挑战，我们提供了两种不同的基于学习的扩散模型来表征多样化的扩散动态，并保证效率和功效。最后，我们提出了一种新颖的目标函数，可以耦合多个约束进行种子节点集推理，可以适应不同的 IM 应用方案。对合成数据集和真实数据集的大量实验和案例研究证明了 DeepIM 相对于现有最先进方法的优势，可以最大限度地扩大影响力传播。