1. 问题

当在window10系统中使用nvidia-smi命令时：

会得到提示：nvidia-smi不是内部或外部命令，也不是可运行的程序或批处理文件。
注：其实安装NVIDIA控制面板时，软件已内置安装了nvidia-smi.exe，我们只需把相关路径添加到环境变量中即可使用相关功能。

2. 解决办法

2.1 查找路径

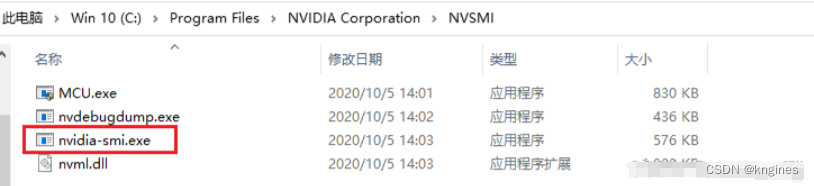
nvidia-smi.exe默认安装路径（也可根据自己的实际安装路径查找）：

C:\Program Files\NVIDIA Corporation\NVSMI

进入该路径下，可看到nvidia-smi.exe可执行程序。

2.2 添加路径至系统环境变量

1、打开“系统属性“ 。

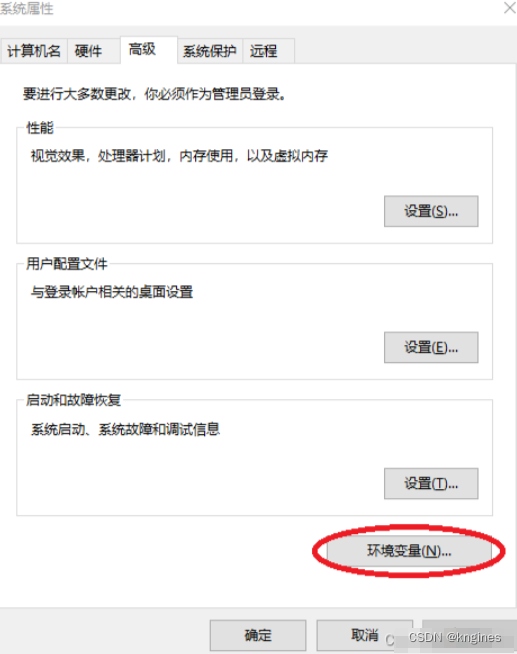
2、配置“环境变量”：

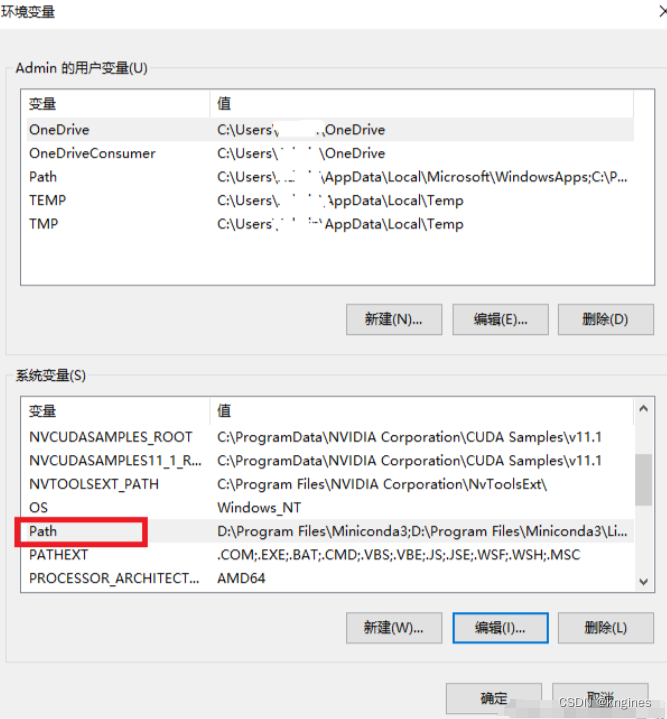
3、添加路径。

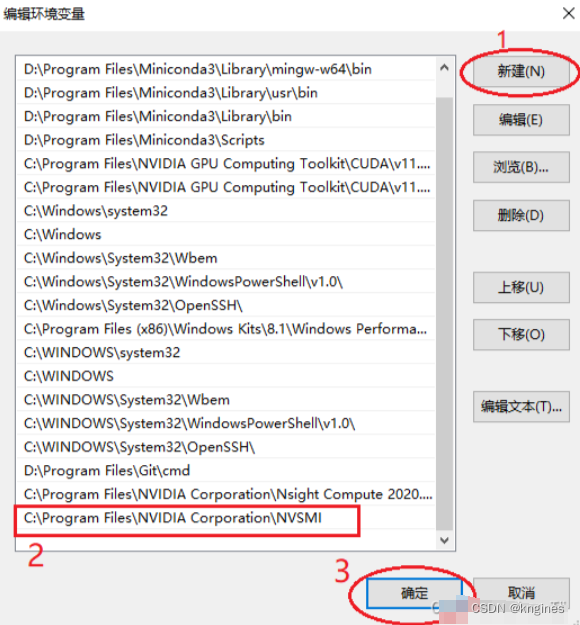
4、保存退出。

3. 使用

重新进入控制台，输入nvidia-smi。即可正常使用。