大家好啊,我是情谊,今天我们来讨论一下按位操作符的知识点与应用,按位操作符有时候在解决一些问题的时候可以提供一个很好的解题思路,话不多说,我们直接来看!
今天我们主要是从两个方面来讲述一下按位操作符的一些特点,一个是详细介绍按位操作符的定义以及一些按位操作符的经典例题,希望能对大家有一些好的建议。
按位操作符:1&按位与操作符 2 | 按位或操作符 3 ^按位异或操作符 4 !按位取反操作符
5<<左移操作符 6 >>右移操作符
开始之前,我们先来介绍一下原码,反码,补码的知识点
整数的二进制位表示方法有三种:原码,反码,补码,有符号的整数在这三种表示方法的基础上还增加了符号位表示和数值位表示,在有符号位的整数中,第一位表示符号位,其余的就表示数值位。
在有符号整数里面,正数的符号位是“0”,负数的符号位是“1”
正整数的原码,反码,补码都是一样的,负数的原码,反码,补码是不一样的
原码:直接将该整数按照正负数的形式翻译为二进制得到的就是原码
反码:将原码的符号不变,其余的数值位依次取反得到的就是反码
补码:在反码的基础上+1就得到了补码
对于一个整型数据来说,在内存中存储的方式其实是反码
至于为什么存储的是反码,那是因为在计算机的系统里面,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理(cpu只有加法器),此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
好了,我们介绍了原码,反码,补码后,我们再来看看移位操作符(注意,移位操作符只能对整数进行操作)
1<<左移操作符
将二进制位除符号位全部左移一个单位,右边用零给补上
我们直接用一个代码来解释

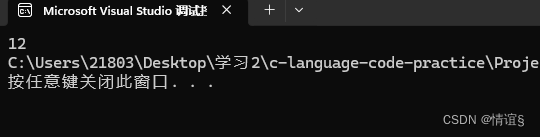
我们可以看到,b的结果是12,为什么会得到这个数呢?我们接着往下看,左移操作符是将a的二进制位向左边移动一位,所以我们先将6的二进制位写出来,(注意哈,我们处理二进制代码的时候依然使用的是补码,但是这里正整数的原,反,补码是相同的,如果处理结果是负数,就要将其转换为二进制的补码再进行操作)00000000000000000000000000000110 ,接下来,我们将整个二进制向左边移动一位,右边空出来的用0补上,得到00000000000000000000000000001100,接着,我们将其转化为十进制的数据,就是12
但是在上面的这个代码中,我们还需要注意的是,<<只是一个操作符,执行并不会改变原来的值,也就是说,a的值并没有被改变,只是执行了左移操作符后将得到的结果赋给了b。


我们来看看负数
-6的原码是10000000000000000000000000000110
符号位不变,取反得到反码 11111111111111111111111111111001
+1得到补码11111111111111111111111111111010
我们再进行左移操作,除符号位其余全部左移一格,得到11111111111111111111111111110100
这个得到的还是补码,我们将其转化为原码就是-12
2右移操作符
右移操作符和左移操作符有部分区别,右移分为两种 操作方式:
1逻辑右移:左边用0填充,右边直接舍弃
2算术右移:左边用符号位进行补齐,右边舍弃
但是具体到底是哪一种,我们要看编译器的实现,常见的编译器都是采用算术右移的
由于前面介绍了左移操作符,所以我们右移操作符就暂时不再提及
3位操作符&,|, ^ ,~
&按位与操作符:整数的二进制位进行比较,都为1才是1,不同的都为0
我们接下来看代码

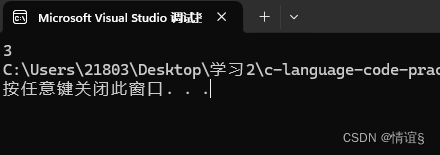
我们来看看这个代码
a是正数,原码,反码,补码相同,所以补码是00000000 00000000 00000000 00000011
b的补码是11111111111111111111111111111011
a&b就是这两个二进制位进行比较,同时是1才是1,其余都是0,得到00000000000000000000000000000011,所以得到的结果是3
|按位或操作符:有1就是1,全是0才是0
我们也直接看代码

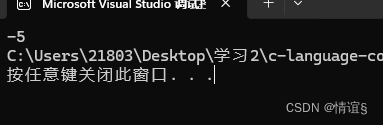
按照规则,3和-5之间的二进制位比较,全是0才是0,有1则就是1
所以得到的补码是1111111111111111111111111111011 ,转换为原码则就是-5
^按位异或:将两个数的二进制位进行比较,相同位0,相异为1
我们也直接看代码


按照规则,相同为0,相异为1,我们可以得到补码11111111111111111111111111111000,再换算为原码后得到10000000000000000000000000001000,就得到-8
~按位取反:对于一个数的二进制位全部进行取反(包括符号位)

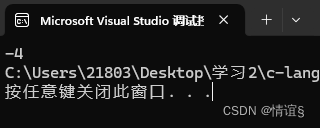
在上面的代码中,我们可以写出3的补码,000000000000000000000000000000011,全部进行取反后得到11111111 11111111 11111111 11111100,得到的是一个数的补码,换算成原码后就是100000000000000000000000000100,就得到了-4
例题介绍
上面我们介绍了这几个操作符后我们在来看看一些具体的例题
1在不创建第三个变量的情况下交换两个数的值
分析:

上面的思路就很好的指明了方式,我们使用a|b,然后将结果再~a^7就可以了

2编写代码实现,求一个数据存储在内存中的二进制中1的个数
n = 13

我们每次让一个数按位与&一个1后,就去除了一个1,然后我们在左移一个操作数,接下来我们可以一直按位与1,循环可以求出1的个数

我们接下来再看一个方法,一个特别经典的方法:使用n&(n-1)
我们假设n = 15
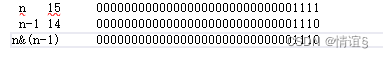
在上面的这个理解中,我们发现n&(n-1)可以得到去除一个1,接下来再次进行
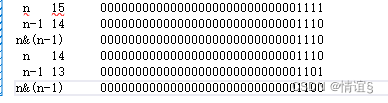
我们可以看到,每进行一次都可以去除一个1,我们统计去除的1的个数就可以计算出1的个数了
,我们来看代码

好了,今天我们的介绍也是在这里了,希望我的一点小的见解能够给你们一点点的帮助,看到这里的小伙伴不如点点赞呗,你们的赞就是对我的最好的鼓励,对了,如果上面文章中出现一些小错误还请担待啦,我会不断进步的,谢谢大家,我们下周见!!
)

前端面試題----歡迎補充)
 intervals的使用)









:python爬虫完整学习大纲)


)

)
