3.1【2369】检查数组是否存在有效划分
2369. 检查数组是否存在有效划分![]() https://leetcode.cn/problems/check-if-there-is-a-valid-partition-for-the-array/
https://leetcode.cn/problems/check-if-there-is-a-valid-partition-for-the-array/
1.这样的判断可以用动态规划来解决,用一个长度为(n+1) 的数组来记录 是否存在有效划分,dp[i] 表示前 i 个元素组成的数组是否至少存在一个有效划分。边界情况 dp[0] 恒为 true而 dp[n] 即为结果。
动态规划的公式为:
这道题目是一个简单的dp,经历了上个月树的一整个月的dfs,bfs的洗礼,盲猜这个月都是dp。
class Solution {
public:bool validPartition(vector<int>& nums) {int n = nums.size();vector<int> dp(n + 1,0);dp[0] = true;for(int i = 1; i <= n; i++){if(i >= 2){dp[i] = dp[i - 2] && validTwo(nums[i - 1],nums[i - 2]);}if(i >= 3){dp[i] = dp[i] || dp[i -3] && validThree(nums[i -3], nums[i -2],nums[i - 1]);}}return dp[n];}bool validTwo(int num1,int num2){return num1 == num2;}bool validThree(int num1, int num2, int num3){return (num1 == num2 && num2 == num3) || (num1 + 1 == num2 && num2 + 1 == num3);}
};3.2【2368】受限条件下可能达到的节点数目
2368. 受限条件下可到达节点的数目![]() https://leetcode.cn/problems/reachable-nodes-with-restrictions/
https://leetcode.cn/problems/reachable-nodes-with-restrictions/
没想到今天的题目又回到了树的遍历问题,和上个月的一道题很像,是一个求邻接表然后进行dfs的题目
-
对于lamda表达式:捕获列表(Capture List):
[&],这表示以引用的方式捕获外部变量。参数列表(Parameter List):(int x, int f),这是lambda函数接受的两个整数参数。返回类型:这里返回类型为void,由于使用了function<void(int,int)>进行了明确的类型声明。 - lamda表示式定义的第二个参数是为了,遍历的时候不往回找,一直往下找。
- 临近表的操作定义二维数组存储即可,做限制的函数一维数组置1即可。
class Solution {
public:int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {//邻接表vector<vector<int>> g(n);for(auto &v : edges){g[v[0]].push_back(v[1]);g[v[1]].push_back(v[0]);}//做限制vector<int> isrestricted(n);for(auto &x : restricted){isrestricted[x] = 1;}int cnt = 0; function<void(int,int)> dfs = [&](int x,int f){cnt ++;for(auto &y : g[x]){if(y != f && !isrestricted[y])dfs(y,x);}};dfs(0,-1);return cnt;}
};3.3【225】用队列实现栈
225. 用队列实现栈![]() https://leetcode.cn/problems/implement-stack-using-queues/
https://leetcode.cn/problems/implement-stack-using-queues/
easy题目,熟悉队列基本操作,还有拓展准备一下一个队列的解法
方法一:两个队列(O(1))
class MyStack {
public:queue<int> q1;queue<int> q2;MyStack() {}void push(int x) {q2.push(x);while(!q1.empty()){q2.push(q1.front());q1.pop();}swap(q1,q2);}int pop() {int r = q1.front();q1.pop();return r;}int top() {return(q1.front());}bool empty() {return(q1.empty());}
};*方法二 一个队列(O(n))
queue<int> q1;MyStack() {} void push(int x) {int n = q1.size();q1.push(x);for(int i = 0; i < n; i++){q1.push(q1.front());q1.pop();}3.4【232】用栈实现队列
232. 用栈实现队列![]() https://leetcode.cn/problems/implement-queue-using-stacks/
https://leetcode.cn/problems/implement-queue-using-stacks/
较为简单,双栈实现队列的push,pop等工作
class MyQueue {
public:stack<int> instack,oustack;MyQueue() {}void push(int x) {instack.push(x);}int pop() {if(oustack.empty()){while(!instack.empty()){oustack.push(instack.top());instack.pop();}}int r = oustack.top();oustack.pop();return r;}int peek() {if(oustack.empty()){while(!instack.empty()){oustack.push(instack.top());instack.pop();}}return oustack.top();}bool empty() {return(instack.empty() && oustack.empty());}
};/*** Your MyQueue object will be instantiated and called as such:* MyQueue* obj = new MyQueue();* obj->push(x);* int param_2 = obj->pop();* int param_3 = obj->peek();* bool param_4 = obj->empty();*/3.6【2917】找出数组中的k-or值
2917. 找出数组中的 K-or 值![]() https://leetcode.cn/problems/find-the-k-or-of-an-array/
https://leetcode.cn/problems/find-the-k-or-of-an-array/
题目难以理解什么意思,主要是按照给的范围遍历位运算
由于给定了nums中元素的范围,我们位从1到31遍历,每一次循环右移i位与1按位与,就是最后一位和1与,记录数目。如果说大于给定的k,对于这个第i位,1向左移动i位和ans按位或 。
class Solution {
public:int findKOr(vector<int>& nums, int k) {int ans = 0;for(int i = 0; i < 31; i++)
{int cnt = 0;;for(int num: nums){if(num >> i & 1 ){cnt ++;}}if(cnt >= k){ans |= 1<<i;}
}
return ans;
}
};3.8【2834】找出美丽数组的最小和
2834. 找出美丽数组的最小和![]() https://leetcode.cn/problems/find-the-minimum-possible-sum-of-a-beautiful-array/
https://leetcode.cn/problems/find-the-minimum-possible-sum-of-a-beautiful-array/
作一个贪心,卡住范围,整体思路就不难了
- 分析题目,按照贪心,要最小和,所以从1开始,按顺序递增的加,但是到二分之target就不能取了,然后就从target依次往后取。
- 根据等差数列求和公式就可以解决
- 注意int不行,要给个long long防止溢出
class Solution {
public:int minimumPossibleSum(int n, int target) {const int mod = 1e9 + 7;int m = target / 2;if(n <= m){return (long long)(1 + n) * n / 2 % mod;}else{return ((long long)(1 + m) * m /2 + ((long long)target + target + (n - m) - 1) * (n - m) /2) % mod;}}
};3.10【299】猜数字游戏
299. 猜数字游戏![]() https://leetcode.cn/problems/bulls-and-cows/
https://leetcode.cn/problems/bulls-and-cows/
今天的题目其实就是一个模拟,熟悉数组存储数据个数。
先把猜对的对应上的数字记录下来,然后如果不对应,用两个数组全部对应,我一开始的思路是先把对应的记录下来,然后删除再去比其他的就要麻烦不少。
用两个数组记录其他的地方出现的数字的个数,最后再通过min,找出猜对了,但是位置不对的个数。
class Solution {
public:string getHint(string secret, string guess) {int bulls = 0;vector<int> cntS(10),cntG(10);for(int i = 0; i < secret.size(); i++){if(secret[i] == guess[i]) {bulls++;}else{++cntG[secret[i] - '0'];++cntS[guess[i] - '0'];}}int cows = 0;for(int i = 0; i < 10;i++){cows += min(cntS[i],cntG[i]);}return to_string(bulls) + 'A' + to_string(cows) + 'B';}
};3.11【2129】将标题首字母大写
2129. 将标题首字母大写![]() https://leetcode.cn/problems/capitalize-the-title/
https://leetcode.cn/problems/capitalize-the-title/
看题目知道是一个模拟题,大小写转换比较经典,如果用c++的话,一句话一句话的模拟会发现确实很麻烦,题解中用到一个l,一个r指向每一个单词的前后端,思路更为清晰
- toupper,tolower大小写字母转换
- 整体思路,while大循环,tittle后边加个空格,防止结尾不同处理。先把r移动到单词的最右边 ,判断单词个数是否需要首字母置为大写,再所有的字母置为小写,最后把最后的空格删掉
class Solution {
public:string capitalizeTitle(string title) {int l = 0,r = 0;int n = title.size();title.push_back(' ');while(r < n){while(title[r] != ' '){r ++;}if(r - l > 2){title[l] = toupper(title[l]);++l;}while(l < r){title[l] = tolower(title[l]);++l;}l = r + 1;++r;}title.pop_back();return title;}
};3.12【1261】在受污染的二叉树中查找元素
1261. 在受污染的二叉树中查找元素![]() https://leetcode.cn/problems/find-elements-in-a-contaminated-binary-tree/
https://leetcode.cn/problems/find-elements-in-a-contaminated-binary-tree/
DFS+哈希表,还原二叉树以后,找target的个数是否大于0
- 用DFS还原二叉树,再判断个数,难度不大
class FindElements {
public:unordered_set<int> valSet;void dfs(TreeNode* node,int val){if(!node){return;}node -> val = val;valSet.insert(val);dfs(node -> left,val * 2 + 1);dfs(node -> right,val * 2 + 2);}FindElements(TreeNode* root) {dfs(root,0);}bool find(int target) {return valSet.count(target) > 0;}
};3.13【2864】最大二进制奇数
2864. 最大二进制奇数![]() https://leetcode.cn/problems/maximum-odd-binary-number/
https://leetcode.cn/problems/maximum-odd-binary-number/
复刷指数:0
简单题,直接模拟
class Solution {
public:string maximumOddBinaryNumber(string s) {int sum = 0;for(int i = 0; i < s.size(); i++){if(s[i] == '1'){sum++;}}string s1;for(int i = 0; i < sum - 1 ;i++){s1.push_back('1');}for(int i = 0; i < s.size() - sum; i++){s1.push_back('0');}s1.push_back('1');return s1;}
};3.14【2789】合并后数组的最大元素
2789. 合并后数组中的最大元素![]() https://leetcode.cn/problems/largest-element-in-an-array-after-merge-operations/
https://leetcode.cn/problems/largest-element-in-an-array-after-merge-operations/
复刷指数:1
倒叙遍历+贪心。难度不大
-
我们从后往前倒序遍历一次数组,依次比较两个相邻的元素,如果两个相邻的元素能够合并,就将其合并。如果不能合并,就继续往前判断。因为这样的操作流程,在比较过程中,靠后的数是所有操作流程可能性中能产生的最大值,而靠前的数,是所有操作流程可能性中能产生的最小值。如果在遍历过程中,比较的结果是不能合并,那么其他任何操作流程都无法合并这两个数。如果可以合并,那我们就贪心地合并,因为这样能使接下来的比较中,靠后的数字尽可能大。
class Solution {
public:long long maxArrayValue(vector<int>& nums) {long long sum = nums.back();for(int i = nums.size() - 2; i >= 0; i--){sum = nums[i] <= sum ? nums[i] + sum : nums[i];}return sum;}
};
3.16【2684】矩阵中移动的最大次数
2684. 矩阵中移动的最大次数![]() https://leetcode.cn/problems/maximum-number-of-moves-in-a-grid/
https://leetcode.cn/problems/maximum-number-of-moves-in-a-grid/
两轮遍历,注意限制索引
- 如果满足要求就让ans等于列数,如果不满足,就把这个地方设为最大值,后边都不会比他大了
- 从第一列开始遍历,因为和前面一列进行比较,这个方法主要是因为搜索过程只能前进不能后退
class Solution {
public:int maxMoves(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();int ans = 0;for(int i = 1; i < n; i++){//列for(int j = 0; j < m; j++){if(grid[j][i] > grid[j][i - 1] || j > 0 && grid[j][i] > grid[j-1][i -1] ||j + 1 < m && grid[j][i] > grid[j + 1][i -1]){//限制索引ans = i;}else{grid[j][i] = INT_MAX;}}}return ans;}
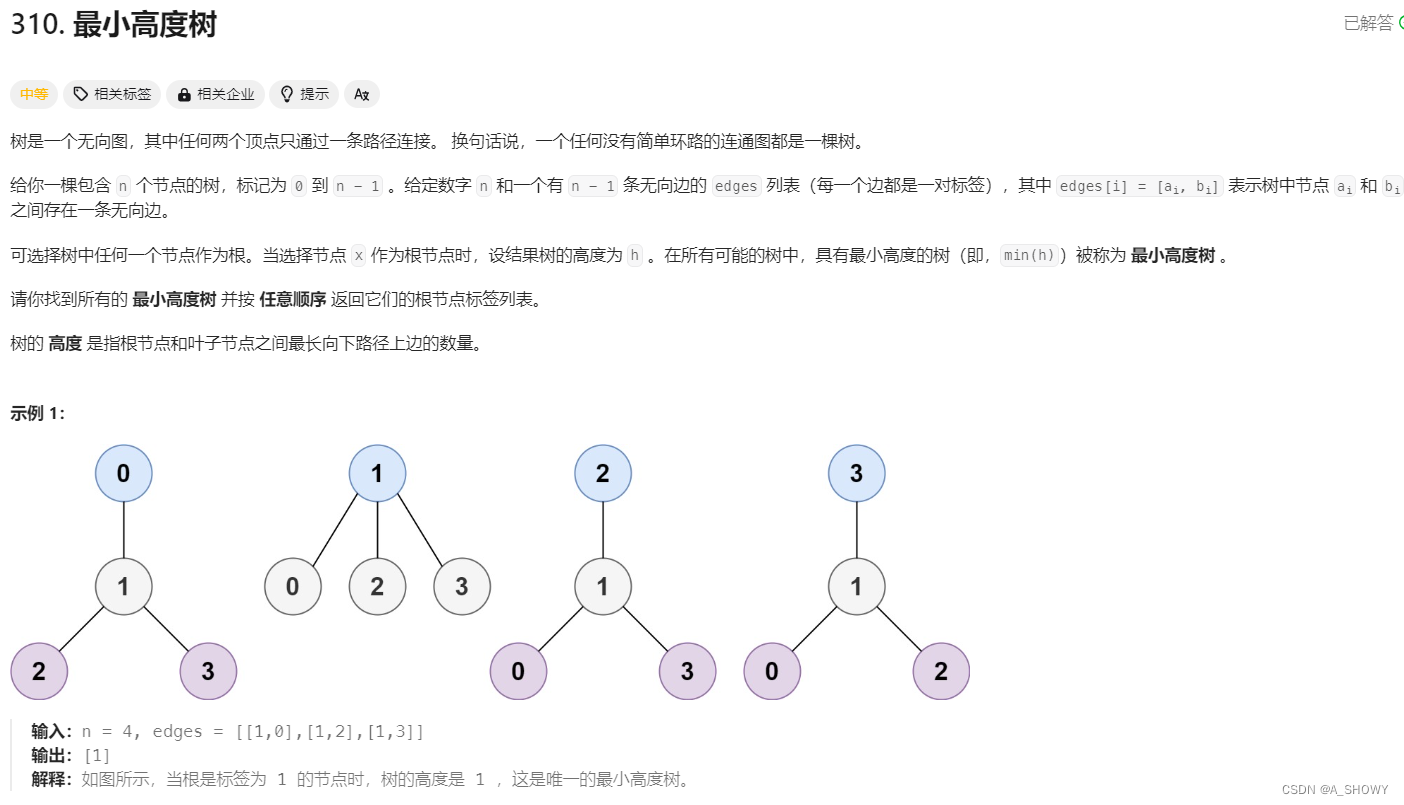
};3.17【310】最小高度树
310. 最小高度树![]() https://leetcode.cn/problems/minimum-height-trees/
https://leetcode.cn/problems/minimum-height-trees/
复刷指数:5
很漂亮的一道题,难度已经是中等题的天花板,是一个从外向内部剥菜的思想,内嵌BFS
- 核心思想:最矮树的根一定不是入度为1的点(画图看下,很容易证明),把最矮树的叶子节点全部减掉,剩下的仍然是最矮树。所以对一个图,不断的把它的叶子节点减掉,减到最后剩下的就一定是最矮树的根。
- 普通思想就是BFS遍历每一个节点,统计每个节点的高度,用map存储起来,查询高度集合中最小的,但是会超时。我们从边缘开始,先找到所有出度为1的节点,然后把所有出度为1的节点进队列,然后不断地bfs,最后找到的就是两边同时向中间靠近的节点,那么这个中间节点就相当于把整个距离二分了,那么它当然就是到两边距离最小的点啦,也就是到其他叶子节点最近的节点了。
class Solution {
public:vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {vector<int> res;if(n == 1){res.push_back(0);return res;}
// 建立度的表vector<int> degree(n,0);vector<vector<int>> map (n,vector<int>());for(auto &edge : edges){degree[edge[0]]++;degree[edge[1]]++;map[edge[0]].push_back(edge[1]);map[edge[1]].push_back(edge[0]);}
// 建立队列,把度为1的点扔进去开始剥皮queue<int> q;for(int i = 0; i < n; i++){if(degree[i] == 1) {q.push(i);}}while(!q.empty()){res.clear();//我们每次要清空,这样最后就剩下最小高度树了int size = q.size();for(int i = 0; i < size; i++){int cur = q.front();q.pop();res.push_back(cur);//把所有当前节点加入结果集vector<int> neighbors = map[cur];//用一个数组接一下//经典BFSfor(int neighbor : neighbors){degree[neighbor] --;if(degree[neighbor] == 1){q.push(neighbor);}}}}return res;}
};









)

算法总结)







)
的使用)

)
利用NVIDIA Triton加速Stable Diffusion XL推理速度)

)

)