目录
概要
一、数据准备
导入数据
数据可视化
二、设计神经网络
版本一
版本二（正片）
三、测试
小结
概要
我的第一个深度学习神经网络模型---利用Pytorch设计人工神经网络对某地区租赁单车的使用情况进行预测
输入节点为1个，隐含层为10个，输出节点数为1的小型人工神经网络，用数据的下标预测单车数量。
PS:
1.该神经网络无法达到解决实际问题的要求，但它结构简单，包含了神经网络的基本元素，可以达到初步入门深度学习以及熟悉Pytorch使用的效果，同时在实践过程中引出了过拟合现象。
2.Pytorch 2.2.1 (CPU) Python 3.6.13|Anaconda 环境
3.《深度学习原理与Pytorch实践》学习笔记
一、数据准备
导入数据
#导入需要使用的库
import numpy as np
import pandas as pd #读取csv文件的库
import matplotlib.pyplot as plt #绘图
import torch
import torch.optim as optim这里我们使用来自GitHub的开源数据用作构建神经网络
#读取数据到内存中，rides为一个dataframe对象
data_path = 'dir/hour.csv' #文件路径
rides = pd.read_csv(data_path)
rides.head() 可以看到成功读入的数据如下：
数据可视化
我们用数据序号(0，1，2，3，···)与数据cnt(count)构建神经网络（hhh实际解决问题时当然不会这样做）
#我们取出最后一列的前50条记录来进行预测
counts = rides['cnt'][:50]#获得变量x，它是1，2，……，50
x = np.arange(len(counts))# 将counts转成预测变量（标签）：y
y = np.array(counts)# 绘制一个图形，展示曲线长的样子
plt.figure(figsize = (10, 7)) #设定绘图窗口大小
plt.plot(x, y, 'o-') # 绘制原始数据
plt.xlabel('X') #更改坐标轴标注
plt.ylabel('Y') #更改坐标轴标注
plt.show()这里我们取出前五十条记录用于模型，绘制出序号与cnt关系，大致数据分布图如下：
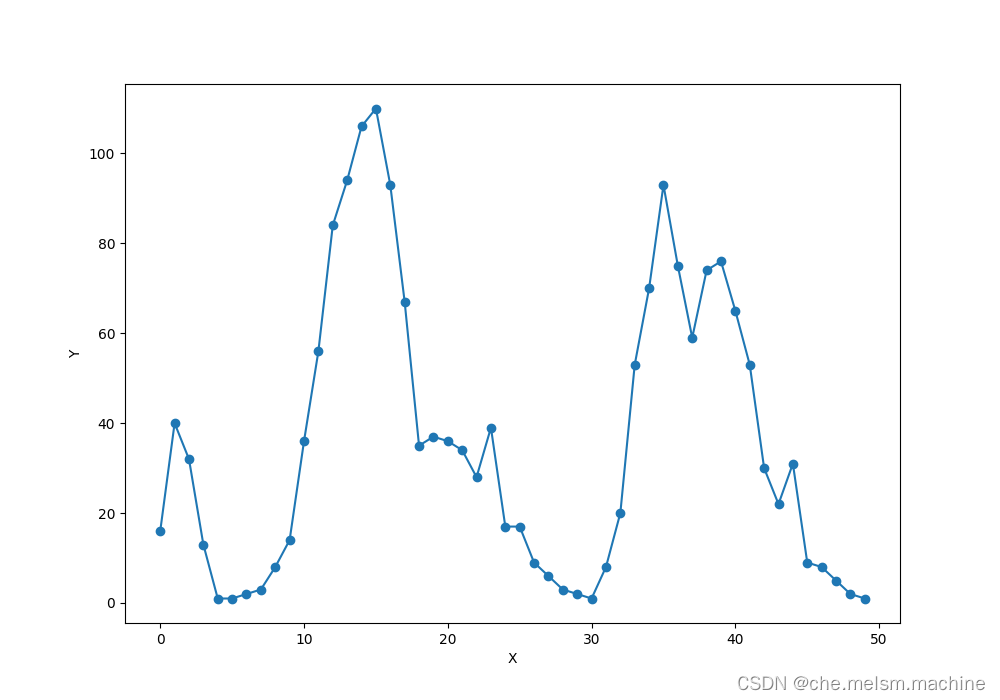
二、设计神经网络
我们构建一个单一输入，10个隐含层单元，1个输出单元的人工神经网络预测器
版本一
#取出数据库中的最后一列的前50条记录来进行预测
counts = rides['cnt'][:50]#创建变量x，它是1，2，……，50
x = torch.tensor(np.arange(len(counts), dtype = float), requires_grad = True)# 将counts转成预测变量（标签）：y
y = torch.tensor(np.array(counts, dtype = float), requires_grad = True)# 设置隐含层神经元的数量
sz = 10# 初始化所有神经网络的权重（weights）和阈值（biases）
weights = torch.randn((1, sz), dtype = torch.double, requires_grad = True) #1*10的输入到隐含层的权重矩阵
biases = torch.randn(sz, dtype = torch.double, requires_grad = True) #尺度为10的隐含层节点偏置向量
weights2 = torch.randn((sz, 1), dtype = torch.double, requires_grad = True) #10*1的隐含到输出层权重矩阵learning_rate = 0.001 #设置学习率
losses = []# 将 x 转换为(50,1)的维度，以便与维度为(1,10)的weights矩阵相乘
x = x.view(50, -1)
# 将 y 转换为(50,1)的维度
y = y.view(50, -1)for i in range(100000):# 从输入层到隐含层的计算hidden = x * weights + biases# 将sigmoid函数作用在隐含层的每一个神经元上hidden = torch.sigmoid(hidden)#print(hidden.size())# 隐含层输出到输出层，计算得到最终预测predictions = hidden.mm(weights2)##print(predictions.size())# 通过与标签数据y比较，计算均方误差loss = torch.mean((predictions - y) ** 2) #print(loss.size())losses.append(loss.data.numpy())# 每隔10000个周期打印一下损失函数数值if i % 10000 == 0:print('loss:', loss)#对损失函数进行梯度反传loss.backward()#利用上一步计算中得到的weights，biases等梯度信息更新weights或biases中的data数值weights.data.add_(- learning_rate * weights.grad.data) biases.data.add_(- learning_rate * biases.grad.data)weights2.data.add_(- learning_rate * weights2.grad.data)# 清空所有变量的梯度值。# 因为pytorch中backward一次梯度信息会自动累加到各个变量上，因此需要清空，否则下一次迭代会累加，造成很大的偏差weights.grad.data.zero_()biases.grad.data.zero_()weights2.grad.data.zero_()运行过程：
程序运行大约14min
# 打印误差曲线
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()打印出误差曲线如下
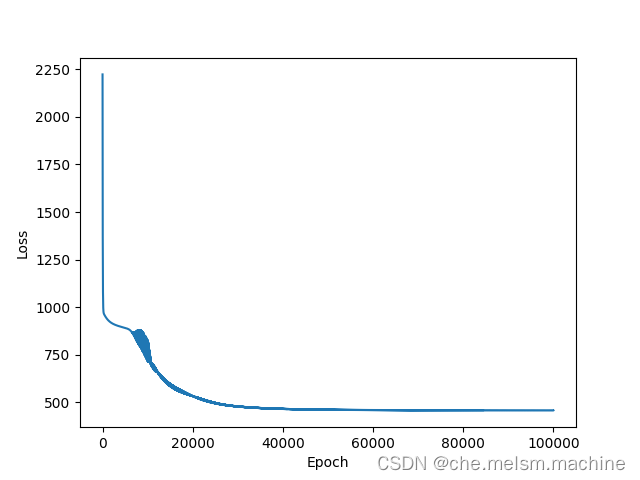
由该曲线可以看出，随着时间的推移，神经网络预测的误差的确在一步步减小。而且，大约到20000步后，误差基本就不会出现明显的下降了
x_data = x.data.numpy() # 获得x包裹的数据
plt.figure(figsize = (10, 7)) #设定绘图窗口大小
xplot, = plt.plot(x_data, y.data.numpy(), 'o') # 绘制原始数据yplot, = plt.plot(x_data, predictions.data.numpy()) #绘制拟合数据
plt.xlabel('X') #更改坐标轴标注
plt.ylabel('Y') #更改坐标轴标注
plt.legend([xplot, yplot],['Data', 'Prediction under 1000000 epochs']) #绘制图例
plt.show()我们可以把训练好的网络对这50个数据点的预测曲线绘制出来，并与标准答案y进行对比：
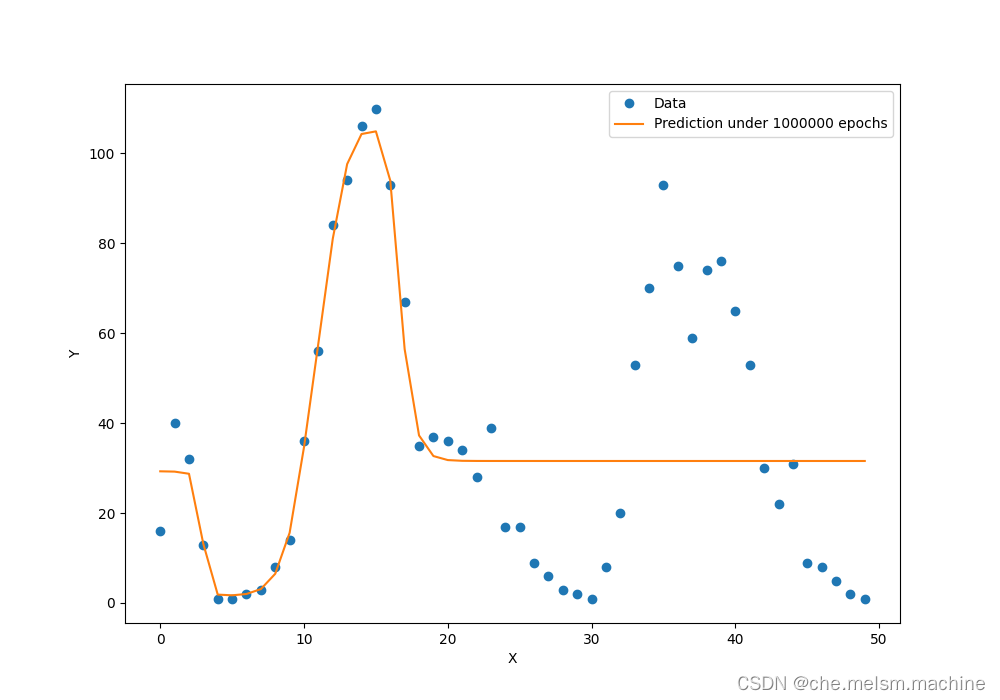
预测曲线在第一个波峰比较好地拟合了数据，但在这之后却偏差较大
版本二（正片）
上面的程序之所以跑得慢，是因为x的取值范围1～50。 而由于所有权重和biases的取值范围被设定为-1,1的正态分布随机数，这样就导致 我们输入给隐含层节点的数值范围为-50~50， 要想将sigmoid函数的多个峰值调节到我们期望的位置需要耗费很多的计算时间
我们的解决方案就是将输入变量的范围归一化
#取出最后一列的前50条记录来进行预测
counts = rides['cnt'][:50]#创建归一化的变量x，它的取值是0.02,0.04,...,1
x = torch.tensor(np.arange(len(counts), dtype = float) / len(counts), requires_grad = True)# 创建归一化的预测变量y，它的取值范围是0～1
y = torch.tensor(np.array(counts, dtype = float), requires_grad = True)#隐藏神经元个数
sz = 10# 初始化所有神经网络的权重（weights）和阈值（biases）
weights = torch.randn((1, sz), dtype = torch.double, requires_grad = True) #1*10的输入到隐含层的权重矩阵
biases = torch.randn(sz, dtype = torch.double, requires_grad = True) #尺度为10的隐含层节点偏置向量
weights2 = torch.randn((sz, 1), dtype = torch.double, requires_grad = True) #10*1的隐含到输出层权重矩阵learning_rate = 0.001 #设置学习率
losses = []# 将 x 转换为(50,1)的维度，以便与维度为(1,10)的weights矩阵相乘
x = x.view(50, -1)
# 将 y 转换为(50,1)的维度
y = y.view(50, -1)for i in range(100000):# 从输入层到隐含层的计算hidden = x * weights + biases# 将sigmoid函数作用在隐含层的每一个神经元上hidden = torch.sigmoid(hidden)# 隐含层输出到输出层，计算得到最终预测predictions = hidden.mm(weights2)# + biases2.expand_as(y)# 通过与标签数据y比较，计算均方误差loss = torch.mean((predictions - y) ** 2) losses.append(loss.data.numpy())# 每隔10000个周期打印一下损失函数数值if i % 10000 == 0:print('loss:', loss)#对损失函数进行梯度反传loss.backward()#利用上一步计算中得到的weights，biases等梯度信息更新weights或biases中的data数值weights.data.add_(- learning_rate * weights.grad.data) biases.data.add_(- learning_rate * biases.grad.data)weights2.data.add_(- learning_rate * weights2.grad.data)# 清空所有变量的梯度值。# 因为pytorch中backward一次梯度信息会自动累加到各个变量上，因此需要清空，否则下一次迭代会累加，造成很大的偏差weights.grad.data.zero_()biases.grad.data.zero_()weights2.grad.data.zero_()
运行程序，耗时约9min
plt.semilogy(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show() 绘出损失曲线：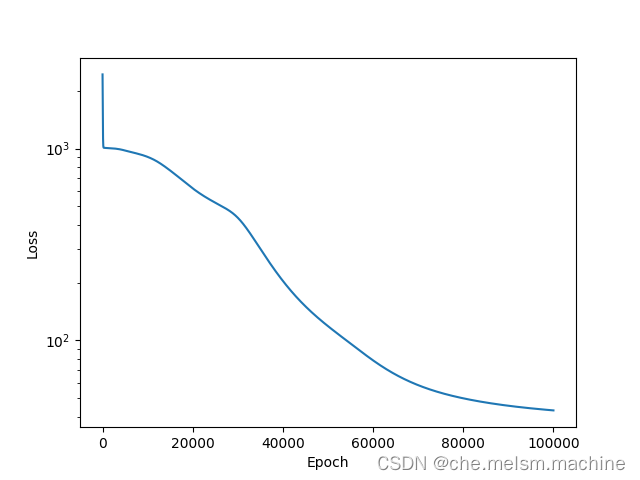
x_data = x.data.numpy() # 获得x包裹的数据
plt.figure(figsize = (10, 7)) #设定绘图窗口大小
xplot, = plt.plot(x_data, y.data.numpy(), 'o') # 绘制原始数据
yplot, = plt.plot(x_data, predictions.data.numpy()) #绘制拟合数据
plt.xlabel('X') #更改坐标轴标注
plt.ylabel('Y') #更改坐标轴标注
plt.legend([xplot, yplot],['Data', 'Prediction']) #绘制图例
plt.show()得到曲线如下：
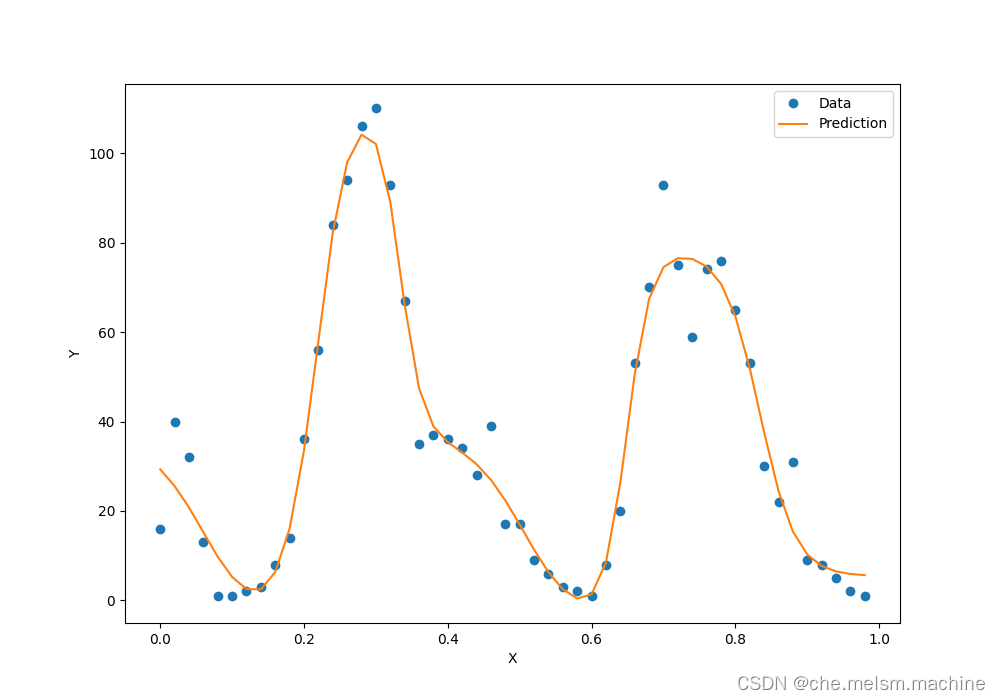
显然拟合效果更好了！
三、测试
我们就需要用训练好的模型来做预测，将后面50条数据(50~100)作为测试集。此时x取值是51, 52, …, 100，同样也要除以50：
counts_predict = rides['cnt'][50:100] #读取待预测的接下来的50个数据点#首先对接下来的50个数据点进行选取，注意x应该取51，52，……，100，然后再归一化
x = torch.tensor((np.arange(50, 100, dtype = float) / len(counts)), requires_grad = True)
#读取下50个点的y数值，不需要做归一化
y = torch.tensor(np.array(counts_predict, dtype = float), requires_grad = True)x = x.view(50, -1)
y = y.view(50, -1)# 从输入层到隐含层的计算
hidden = x * weights + biases# 将sigmoid函数作用在隐含层的每一个神经元上
hidden = torch.sigmoid(hidden)# 隐含层输出到输出层，计算得到最终预测
predictions = hidden.mm(weights2)# 计算预测数据上的损失函数
loss = torch.mean((predictions - y) ** 2)
print(loss)x_data = x.data.numpy() # 获得x包裹的数据
plt.figure(figsize = (10, 7)) #设定绘图窗口大小
xplot, = plt.plot(x_data, y.data.numpy(), 'o') # 绘制原始数据
yplot, = plt.plot(x_data, predictions.data.numpy()) #绘制拟合数据
plt.xlabel('X') #更改坐标轴标注
plt.ylabel('Y') #更改坐标轴标注
plt.legend([xplot, yplot],['Data', 'Prediction']) #绘制图例
plt.show()得到结果如下：
直线是我们的模型给出的预测曲线，圆点是实际数据所对应的曲线。
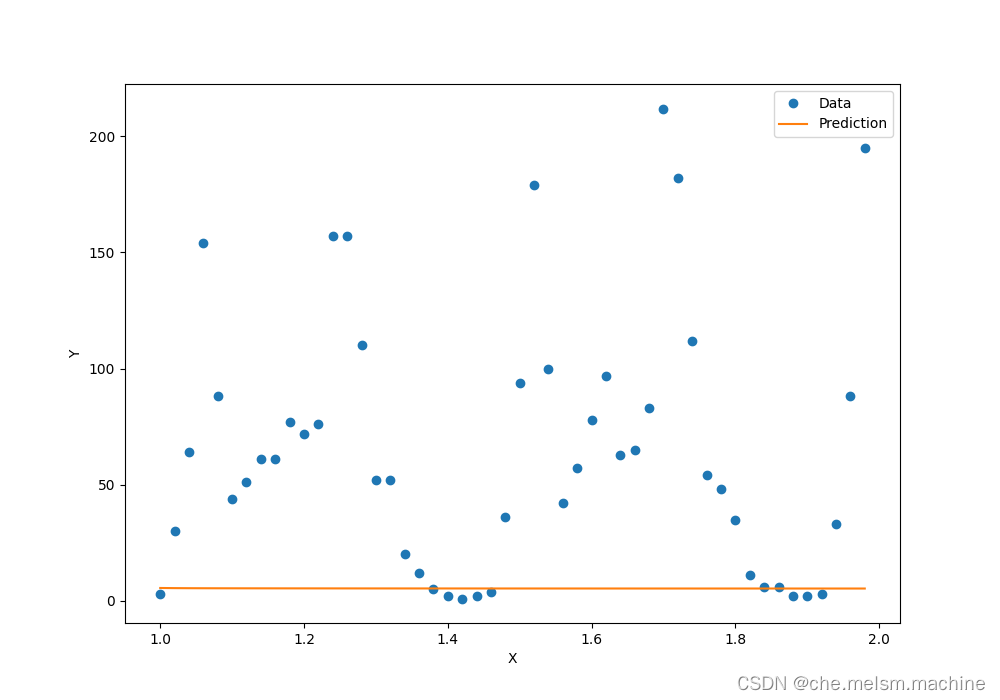模型预测与实际数据竟然完全对不上！为什么我们的神经网络可以非常好地拟合已知的50个数据点，却在测试集上出错了呢？因为y（单车数量）与x（数据序号）根本没有关系！这就是在机器学习中最常见的困难---过拟合
过拟合（Overfitting）是指机器学习模型在训练数据上表现很好，但在测试数据上表现较差的情况。过拟合通常发生在模型过度复杂或者训练数据量太少的情况下。
对于我们的单车预测模型，问题显然在于我们要求模型学习 单车数量y 与 数据序号x 之间的关系，模型通过学习我们给出的前五十组数据（训练集）学会了它所认为的样本特征，但当我们引入后面50组样本（测试集）时，我们发现模型学到的特征是没有意义的，它只能反映训练集中的某些特点。
如果要解决这个问题，我们就应该让模型学习关于样本的更多特征，如：星期几、是否节假日、温度、湿度等（显然这些才是真正会影响x的因素）。当然从理论上讲，这样得到的神经网络更复杂，但显然他的预测更能达到我们想要的效果。
小结
对于我们的单车预测模型，问题显然在于我们要求模型学习 单车数量y 与 数据序号x 之间的关系，模型通过学习我们给出的前五十组数据（训练集）学会了它所认为的样本特征，但当我们引入后面50组样本（测试集）时，我们发现模型学到的特征是没有意义的，它只能反映训练集中的某些特点。
如果要解决这个问题，我们就应该让模型学习关于样本的更多特征，如：星期几、是否节假日、温度、湿度等（显然这些才是真正会影响x的因素）。当然从理论上讲，这样得到的神经网络更复杂，但显然他的预测更能达到我们想要的效果。
主要参考资料：《深度学习原理与Pytorch实践》
参考代码：bike1.py · che.melsm/DeepLearning Project - Gitee.com
