卷积神经网络
基本结构
首先解释一下什么是卷积,这个卷积当然不是数学上的卷积,这里的卷积其实表示的是一个三维的权重,这么解释起来可能不太理解,我们先看看卷积网络的基本结构。
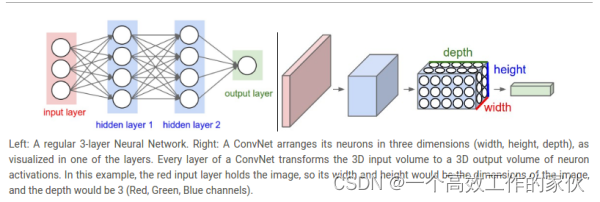
通过上面的图我们清楚地了解到卷积网络和一般网络结构上面的差别,也可以理解为卷积网络是立体的,而一般的网络结构是平面的。
卷积层
了解完了基本的结构之后,我们就要了解cnn最重要的一个部分,也是起最为创新的一个部分,卷积层。首先用一张图片来比较一下卷积网络到底创新在什么地方。
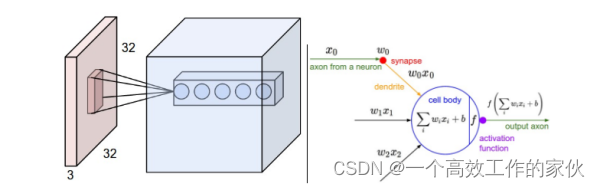
我们通过这个结构就可以清晰地看到卷积网络到底是怎么实现的。首先右边是传统的网络结构,在上一篇文章中我们已经详细的解释过了。而左边的图片,我们首先看看图中最左边的结构,你肯定会好奇为什么是32x32x3的一块立体方块。这个32×32代表的是像素点,说白了也就是图片的大小,这个大小是你可以设置的,你可以设置为50×50,也可以是256×256,这都取决与图片的大小,那么3表示什么呢?3其实表示的是RGB的三个通道,RGB也是什么?RGB表示red,green,blue,这三种颜色的各种组合叠加可以形成各种各样的颜色,所以任何一张照片都可以用左边这种图形来表示。
那么中间这个小方块又表示什么呢?这个就是我们要重点讲的卷积。所谓的卷积,就是这种小方块,我们设置一个小方块的大小,但是这个小方块的厚度必须和左边的这个大方块的厚度是一样的,大方块每一个像素点由一个0到255的数字表示,这样我们就可以赋予小方块权重,比如我们取小方块的大小是3×3,我们要求起厚度必须要和左边的大方块厚度一样,那么小方块的的大小就为3x3x3,我们就可以赋予其3x3x3个权重,然后我们就可以开始计算卷积的结果,将小方块从大方块的左上角开始,一个卷积小方块所覆盖的范围是3x3x3,然后我们将大方块中3x3x3的数字和小方块中的权重分别相乘相加,再加上一个偏差,就可以得到一个卷积的接过,可以抽象的写成Wx b这种形式,这就是图上所显示的接过,然后我们可以设置小方块的滑动距离,每次滑动就可以形成一个卷积的计算结果,然后讲整张大图片滑动覆盖之后就可以形成一层卷积的结果,我们看到图中的卷积结果是很厚的,也就是设置了很多层卷积。总结来说,就是每层卷积就是一个卷积核在图片上滑动求值,然后设置多个卷积核就可以形成多层的卷积层。
池化层
讲完卷积层,接下来就要讲一下池化层。为什么会有池化层的出现呢?是因为不断的做卷积,得到的中间结果会越来越厚,卷积就相当于提取图片中的特征,所以卷积层一般会设置得越来越厚,不然你就无法从前面的接过来提取更多的特征。这样就会导致中间的结果会越来越大,计算会越来越慢,所以提出了池化层。
所谓的池化层,就是将图片的大小缩小的一种处理方式。我们可以先看看下面的图片。
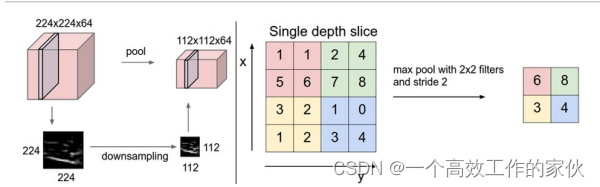
通过这个图片,我们可以清楚地看到池化层是怎么处理的。池化层也是需要先设置一个窗口,但是这个小窗口的厚度是1,而不再是前一层输出的结果的厚度。然后有两种处理方式,一种是取这个小窗口里面所有元素的最大值来代表这个小窗口,一种是取平均值,然后将小窗口滑动,在第二的位置再做同样的处理,上层网络输出方块的每一层做完之后就进入这个大方块的下一层做同样的操作,这个处理办法就可以让整个大方块的大小变小,可以看看上面的图片的左边。右边是一个简单的一层厚度,取最大值的例子。
Code
数据集仍然是使用MNIST手写字体,和之前一样做同样的预处理。
Model
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | # 定义 Convolution Network 模型 class Cnn(nn.Module): def __init__(self, in_dim, n_class): super(Cnn, self).__init__() self.conv = nn.Sequential( nn.Conv2d(in_dim, 6, 3, stride=1, padding=1), nn.ReLU(True), nn.MaxPool2d(2, 2), nn.Conv2d(6, 16, 5, stride=1, padding=0), nn.ReLU(True), nn.MaxPool2d(2, 2), ) self.fc = nn.Sequential( nn.Linear(400, 120), nn.Linear(120, 84), nn.Linear(84, n_class) ) def forward(self, x): out = self.conv(x) out = out.view(out.size(0), -1) out = self.fc(out) return out model = Cnn(1, 10) # 图片大小是28x28 use_gpu = torch.cuda.is_available() # 判断是否有GPU加速 if use_gpu: model = model.cuda() # 定义loss和optimizer criterion = nn.CrossEntropyLoss() optimizer = optim.SGD(model.parameters(), lr=learning_rate) |
以上就是网络的模型的部分了。和之前比主要增加了这些不一样的部分
- 1 nn.Sequential()
这个表示将一个有序的模块写在一起,也就相当于将神经网络的层按顺序放在一起,这样可以方便结构显示 - 2 nn.Conv2d()
这个是卷积层,里面常用的参数有四个,in_channels, out_channels, kernel_size, stride, padding
in_channels表示的是输入卷积层的图片厚度out_channels表示的是要输出的厚度
kernel_size表示的是卷积核的大小,可以用一个数字表示长宽相等的卷积核,比如kernel_size=3,也可以用不同的数字表示长宽不同的卷积核,比如kernel_size=(3, 2)
stride表示卷积核滑动的步长
padding表示的是在图片周围填充0的多少,padding=0表示不填充,padding=1四周都填充1维
- 3 nn.ReLU()
这个表示使用ReLU激活函数,里面有一个参数inplace,默认设置为False,表示新创建一个对象对其修改,也可以设置为True,表示直接对这个对象进行修改 - 4 nn.MaxPool2d()
这个是最大池化层,当然也有平均池化层,里面的参数有kernel_size, stride, paddingkernel_size表示池化的窗口大小,和卷积层里面的kernel_size是一样的
stride也和卷积层里面一样,需要自己设置滑动步长
padding也和卷积层里面的参数是一样的,默认是0
模型需要传入的参数是输入的图片维数以及输出的种类数
train
训练的过程是一样的,只是输入图片不再需要展开
这是训练20个epoch的结果,当然你也可以增加训练次数,修改里面的参数达到更好的效果,可以参考一下Lenet的网络结构,自己重新写一写
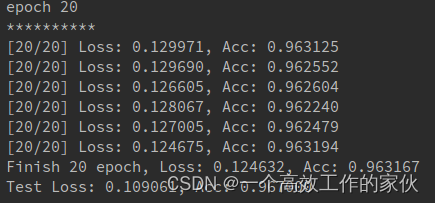
大体上简单的卷积网络就是这么构建的,当然现在也有很多复杂的网络,比如vgg,inceptionv1-v4,resnet以及修正的inception-resnet,这些网络都是深层的卷积网络,有兴趣的同学可以去看看pytorch的官方代码实现,或者去github上搜索相应的网络。
下一节我们将要开始一种特别适合序列数据的新的网络结构,循环神经网络。





)
![[C++]AVL树怎么转](http://pic.xiahunao.cn/[C++]AVL树怎么转)
(上))
)

Selected Level Actor节点升级到UE5)








