专栏导读
- 作者简介:工学博士,高级工程师,专注于工业软件算法研究
- 本文已收录于专栏:《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法,并提供所有案例完整源码;2.复杂函数包含:分段函数、积分函数、常/偏微分函数、隐函数、方程组、级数函数、多参数函数;3.拟合工具是Matlab种的lsqcurvefit, nlinfit,神经网络,ga遗传算法,MultiStart全局优化算法等;4.拟合案例均源自科研实践中遇到的案例,文本教程+视频教程+案例源码,三向强化学习!提高大家解决实际数学建模的问题。
- 【案例源码地址】Matlab偏微分方程拟合 | 源码分享 | 视频教程
- 【视频课程地址】https://www.bilibili.com/video/BV1bQ4y1U7mu/?spm_id_from=333.337.search-card.all.click
- 欢迎订阅专栏,订阅用户可私聊进入Matlab编程交流群(知识交流、问题解答),并获赠丰厚的Matlab相关学习资料(教材、源码、视频课)
- 专栏订阅地址:https://blog.csdn.net/u010542847/category_12576325.html
文章目录
专栏导读
文章目录
【总体简介】💻🔍
【代码截图】
【视频课程】
【总体简介】💻🔍
你将获得: 偏微分方程拟合matlab源码 + 参考论文+视频教程
程序实现了偏微分方程中参数的拟合,具体函数形式如下图所示,函数的自变量是t,因变量是I(t),被积函数中包含的n(s,t)是通过偏微分方程求解得到,待拟合参数为k1,k2, D, s0, sL,拟合采用的工具是lsqcurvefit(),难点在于如何定义拟合函数,包含了积分运算,偏微分方程运算等内容,非常复杂。但是程序成功实现了该复杂函数的拟合。该案例源自一篇论文中的模型,也随代码一起提供给用户。
建议小伙伴在学习偏微分方程拟合前,先学习一下Matlab偏微分方程求解的课程(见文末链接)。
代码文件包含(见后文代码截图):1.实验数据离散点文件;2.main主文件;3.自定义拟合函数文件;4.偏微分方程的定义函数;5.偏微分方程边界条件定义函数

【代码截图】
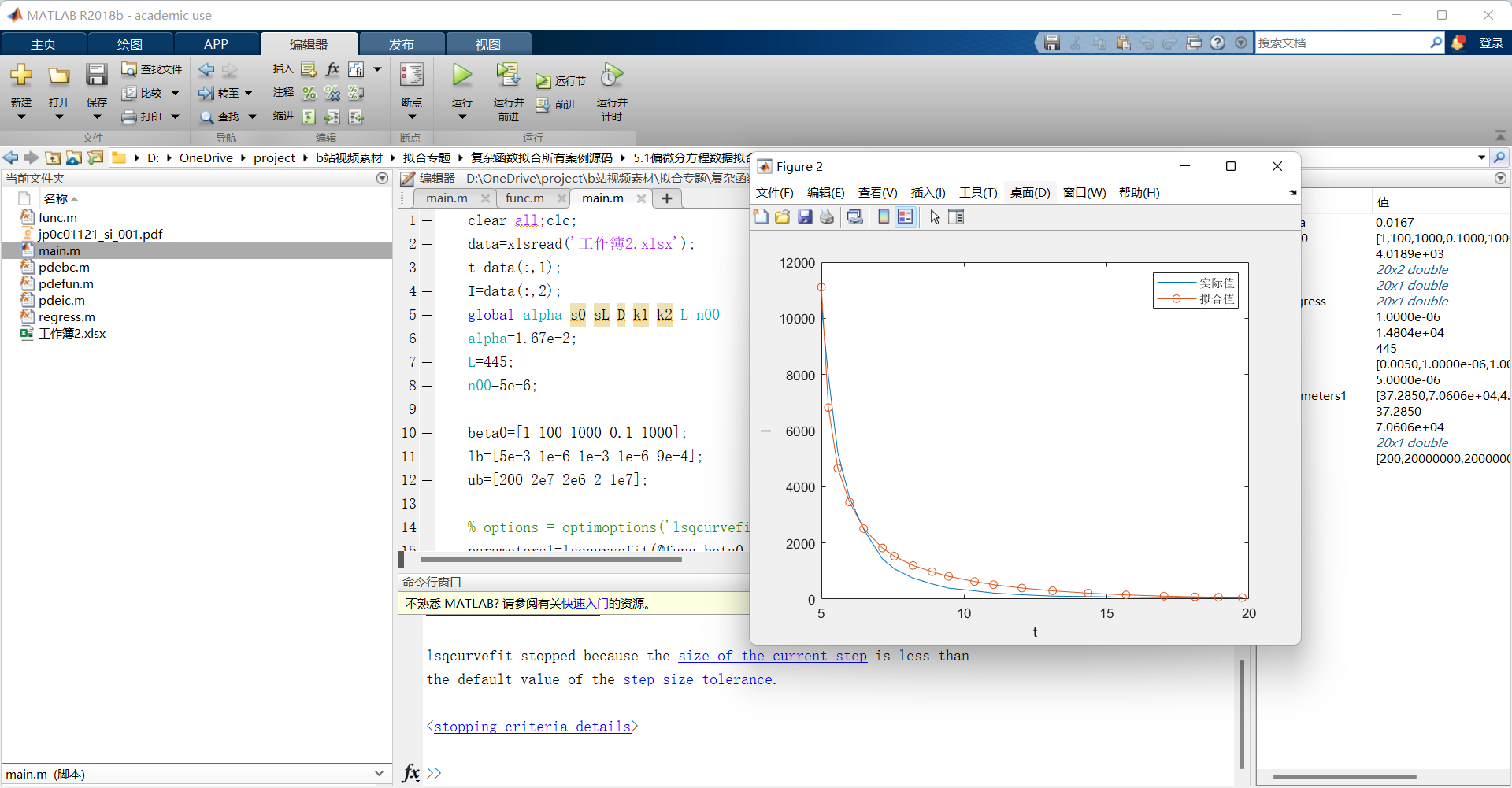
【视频课程】
【Matlab复杂函数非线性拟合专题/lsqcurvefit/nlinfit/分段函数、积分函数、常/偏微分函数、隐函数、方程组、最小二乘法/机器学习/神经网络/编程/人工智能】 3.(试看)积分函数拟合(被积函数存在待定参数+积分上下限为自变量)_哔哩哔哩_bilibili


)
















