2673. 使二叉树所有路径值相等的最小代价

题目描述：

给你一个整数 n 表示一棵 满二叉树 里面节点的数目，节点编号从 1 到 n 。根节点编号为 1 ，树中每个非叶子节点 i 都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1 。

树中每个节点都有一个值，用下标从 0 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1 个节点的值。每次操作，你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。

注意：

• 满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个子节点，且所有叶子节点距离根节点距离相同。
• 路径值 指的是路径上所有节点的值之和。

示例 1：

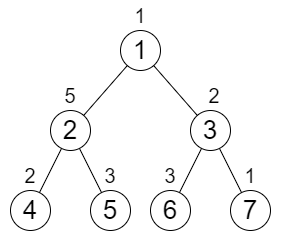
输入：n = 7, cost = [1,5,2,2,3,3,1]
输出：6
解释：我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

示例 2：

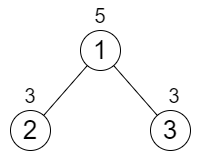
输入：n = 3, cost = [5,3,3]
输出：0
解释：两条路径已经有相等的路径值，所以不需要执行任何增加操作。

提示：

• 3 <= n <= 10^5
• n + 1 是 2 的幂
• cost.length == n
• 1 <= cost[i] <= 10^4

思路：

首先对于满二叉树来说，他可以支持随机读取，对于非叶子节点，2i为左孩子，2i+1为有孩子，(i)下取整为父节点。

根据题意，我们可知应该要将所有路径上的权值和按照最大的那个路径和来进行补齐。

（1）
考虑根到两个互为兄弟节点（父节点相同）的叶子的两条路径。

由于这两条路径除了叶子节点不一样，其余节点都一样，所以为了让这两条路径的路径和相等，必须修改叶子节点的值。

设叶子节点的值分别为 x 和 y，假设 x≤y，是否需要同时增加 x 和 y 呢？

这是不需要的，把 x增加 y−x就行，因为我们可以增加它们的祖先节点的值，使得它们俩的路径和与其它的路径和相等，这样可以节省操作次数。

（2）
对于不是叶子的兄弟节点，又要如何比较和计算呢？和上面的分析一样，从根到当前节点的路径，除了这两个兄弟节点不一样，其余节点都一样。所以把路径和从叶子往上传，这样就可以按照提示 1 那样比较了。

代码：

class Solution {public int minIncrements(int n, int[] cost) {int res=0;for(int i=n/2;i>0;i--){//从最后一个非叶子节点开始算;自底向上res+=Math.abs(cost[2*i-1]-cost[2*i]);//两个非叶节点变成一样的cost[i-1] += Math.max(cost[i*2-1],cost[2*i]);//累加路径和}return res;}
}