论文解读--Mutual Interference Mitigation in PMCW Automotive Radar

PMCW汽车雷达的相互干扰抑制

摘要

针对相位调制连续波(PMCW)毫米波(mmWave)汽车雷达系统中存在的相互干扰问题进行了研究。对先进驾驶辅助系统(ADAS)的需求日益增长，导致配备在同一频段工作的毫米波雷达系统的车辆激增，导致相互干扰，可能会降低雷达性能，从而产生安全隐患。我们考虑了涉及两个相似PMCW雷达系统的场景，并提出了一种有效的发射波形协同设计技术，使它们之间的相互干扰最小化。通过毫米波汽车雷达系统的仿真对所提出的方法进行了数值评估。结果表明，该技术显著减少了相互干扰，提高了雷达探测性能，同时对实际汽车雷达系统的计算成本非常低，对现有基础设施的影响微不足道。

1 介绍

毫米波(mmWave)汽车雷达系统由于其在具有挑战性的环境中精确的目标检测能力而获得了极大的关注。与相机和激光雷达相比，毫米波雷达系统在大雨、雾、雪和烟雾中表现出色[1]，[2]。这些系统在77 GHz到81 GHz的频率范围内工作，利用高频连续波(CW)进行目标检测。然而，它们较差的角分辨率限制了精细空间细节的检测。多输入多输出(MIMO)技术可以提高分辨率，但也会带来相互干扰的挑战。

当多个发射机在近距离工作时，MIMO雷达系统会产生相互干扰，导致底噪增加，检测精度和可靠性降低。先进的信号处理技术，如数字波束形成和自适应滤波可以缓解这个问题[3]。随着车载雷达系统数量的增加和毫米波频段的拥塞，相互干扰问题日益突出[4]。调制技术，如调相连续波(PMCW)和正交频分复用(OFDM)，与传统的调频连续波(FMCW)相比具有优势，但它们需要更高的采样率和复杂的收发器硬件[5]。

相互干扰抑制的研究主要集中在FMCW雷达系统的波形设计上[6]-[10]。已经提出了用于慢时间或快时间信号的自适应波形，包括慢时间编码波形、快速生成的自适应慢时间编码方案和快时间编码方案[11]。伪正交噪声波形和专门的慢时波形，如黄金码和线性调频CAZAC码也被探索过[8]-[10]。

本文主要研究了PMCW雷达间相互干扰的抑制问题。虽然研究已经解决了FMCW和PMCW雷达之间的相互干扰问题(参见[12]-[15]以及其中的参考文献)，但在PMCW系统的波形设计方面存在研究空白，特别是当雷达系统具有相似的物理参数时。为了解决这一差距，提出了一种设计协同波形的新框架。该框架可以处理非凸目标，在实际实现中计算效率高，并且需要对收发器基础结构进行最小的修改。

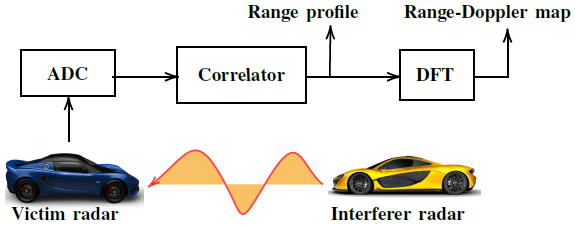
图1:PMCW雷达工作和两车PMCW-PMCW相互干扰的简化示意图。

2 问题公式化

A PMCW信号模型

在本节中，我们建立了PMCW雷达模型。我们考虑两个PMCW汽车雷达系统，如图1所示，它们相似且相互合作。这些雷达在同一频带内工作。两个PMCW雷达在单次触发信号中的发射信号可以描述为

(1)

其中，fc是载波频率，T是脉冲重复间隔（PRI），φ(t)是调制相位波形[4]。如果chirp持续时间是Tc，我们在kTc≤t≤(k +1)Tc区间内，用表示第k个chirp的相移，得到。我们假设在一个相干处理间隔(CPI)内传输N个信号触发。因此，发射信号为

(2)

其中，0≤t≤NT，同时

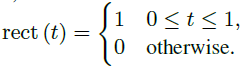(3)

我们考虑一个单一目标，位于距离R处，以速度v向雷达移动，它将雷达信号反射回来。双向目标传播延迟为τT (t)= ，其中c为光速。接收信号为

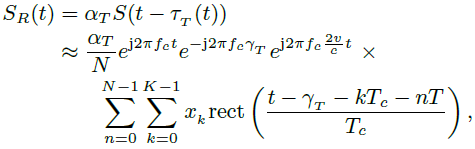(4)

这里我们假设v ≪ c作为近似。假设两台雷达的协同性能消除了接收机的载波频偏（CFO）。将接收信号SR(t)与载波频率的共轭混合后，我们假设项和αT抵消了。我们把表示为多普勒频率，得到

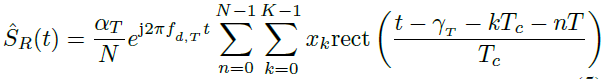(5)

如图1所示，在ADC中，时间分为快时间t′和慢时间索引n，时间间隔t为t = t′+ nT, t′∈[0,t]，在快时间中，信号可以间隔Tc采样，即在t′= mTc处，得到

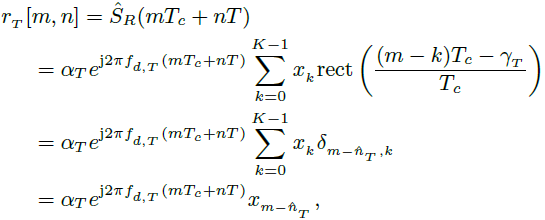(6)

其中δi,j是克罗内克函数的扩展

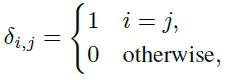（7）

而是在距离R处由于目标引起的编码位移。如图1所示，在接收机中，(6)中的离散信号将通过相关器产生距离曲线。(6)与(2)的相关性为

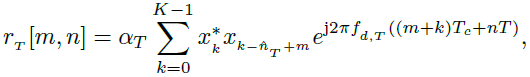(8)

其为目标的距离分布[13]。第二个雷达的影响，作为一个干扰，对在受害雷达中观察到的距离分布表示在下面的模型中。

B 相关干扰模型

受害雷达系统从干扰雷达发射机接收信号，该信号可以被接收机错误地解释为来自目标的反射信号。两台雷达发射PMCW时的这种干扰称为PMCW-PMCW干扰[16]。在本节中，干扰PMCW雷达系统，发射的信号相位码为，假设与(2)类似的干扰受害雷达发射相位码为的PMCW信号。我们将与干扰相关的单向延迟定义为，其中RI是两个雷达系统之间的距离，vI是两个雷达系统之间的相对速度。设为与干扰相关的多普勒频率。受害雷达接收机的干扰采样为

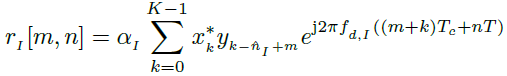（9）

其中，为干扰引起的编码位移。值得强调的是，两台雷达的协同性能使我们能够有效地补偿它们之间的去同步和不同的PRI。

3 相互干扰缓解

接收信号用公式表示为

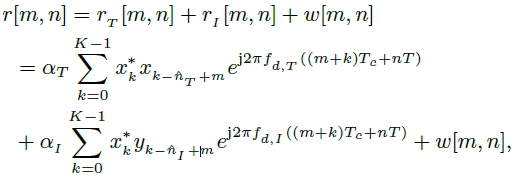(10)

其中w[m, n]表示与信号无关的干扰，如接收机噪声。在接收器中，(10)将通过对慢时间样本应用离散傅里叶变换(DFT)进行多普勒处理器处理。因此，距离-多普勒图是

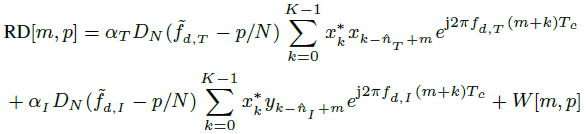（11）

其中，是Dirichlet函数。移动的目标会改变chirp的相位。这种现象由式(11)中的项表示。因此，接收到的序列将不是纯二进制序列。这种对多普勒引起的相移的敏感性被称为多普勒不容忍[18]，在如图2所示的距离曲线上产生了小的旁瓣。我们也很容易知道，对于PMCW雷达，距离-多普勒估计是不耦合的[13]。

如[12]所述，与快时间处理的时间尺度相比，典型的多普勒频率非常低，即fd,I≪1/Tc。从(11)中可以明显看出，干扰是由每个距离bin中的相互关系缩放的。我们定义

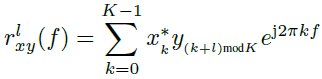(12)

。由式(11)可以证明，对于，是一个优势干扰项。为了减轻两雷达系统之间的相互干扰，我们提出抑制干扰功率。因此，我们考虑以下关于两个编码x和y的优化问题:

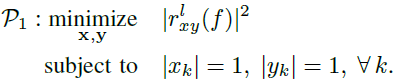（13）

在实际场景中，车辆上的被害者雷达和干扰雷达是异步传输的，和都不知道。因此，我们寻求将多个网格点上的干扰最小化

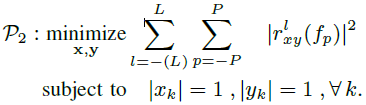(14)

P的值由感兴趣的最大多普勒频率决定。引起编码位移的干扰距离根据的关系影响许多距离bin，因此我们选择足够大的L以减轻所有距离bin的干扰影响。

备注1。(12)中的表达式可以改写为

(15)

其中，

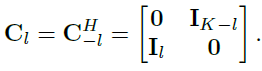(16)

由于单模性约束，优化问题(14)是非凸的。在此，我们建议以循环的方式解决这个问题。具体来说，在我们的循环优化算法的第s次迭代中，我们首先对固定的优化x，并设置最优解为。然后，在其他条件不变的情况下，我们对固定的优化y。在下文中，我们给出了每个迭代中涉及的两个子问题的解决方案。但首先，我们评论了非模二次规划(UQPS)和幂方法(PMLI)迭代来解决这类问题。

备注2。UQP定义为

（17）

其中为单模向量的集合。第s次PMLI迭代时的单模向量序列

(18)

导致当G是正定矩阵时，UQP的目标值单调递增。此外，在不改变最优解的情况下，采用对角加载技术保证了矩阵的正定性。特别地，在(17)中，对角线加载， λm略大于G的最大特征值，导致了一个等价问题，给我们留下了一个正定的eG[19]。

•固定y下x的优化:将(15)代入(14)，相关问题变为

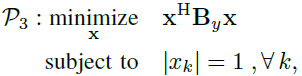（19）

其中。通过备注2介绍的对角加载技术，我们得到了正定矩阵，得到了等效问题

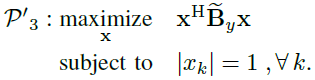（20）

•固定x下 y的优化:关于y的问题，稍作修改，是

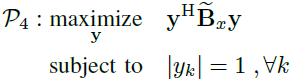(21)

。

我们循环优化子问题P'3和P4，直到收敛。每个子问题都通过在备注2中介绍的PMLI迭代来解决。算法1总结了该算法的步骤。(14)在迭代s时的目标值用表示。在下文中，我们对所提出的算法进行了数值评估。

算法1 PMCW波形的相互干扰抑制设计

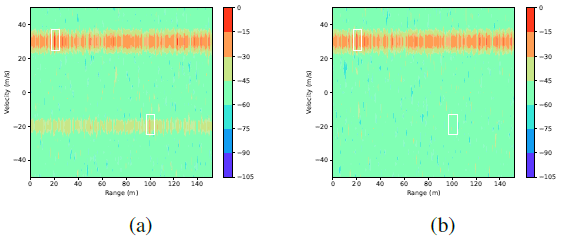
图2:a)随机PMCW信号和b)算法1生成的PMCW波形的单个目标距离-多普勒图。

4 数值评估

我们考虑了两辆装有雷达的车辆，雷达发射PMCW波形，工作频率为fc = 79 GHz，脉冲持续时间为T = 6.66 ns。发射N = 140个触发信号，在接收信号中加入分布为的高斯白噪声，假设目标和干扰RCS为35 dBsm。目标放置在距离R = 20 m处，以速度v = 30 m/s移动。假设干扰雷达位于距离RI = 200 m处，相对速度vI =−20 m/s。如图2 (a)和(b)所示，分别采用算法1随机生成K = 50个chirp的PMCW波形，目标场景的二维距离多普勒图像。可以看到，在图2(a)中，干扰的功率很强，导致虚警。优化后的PMCW波形可以有效地抑制干扰，从而提高雷达的目标探测性能。