至于枚举
会用就行 至少目前我感觉没什么太多问题
enum 被称为无作用域枚举 , enumclass / enumstruct 被称为有作用域枚举
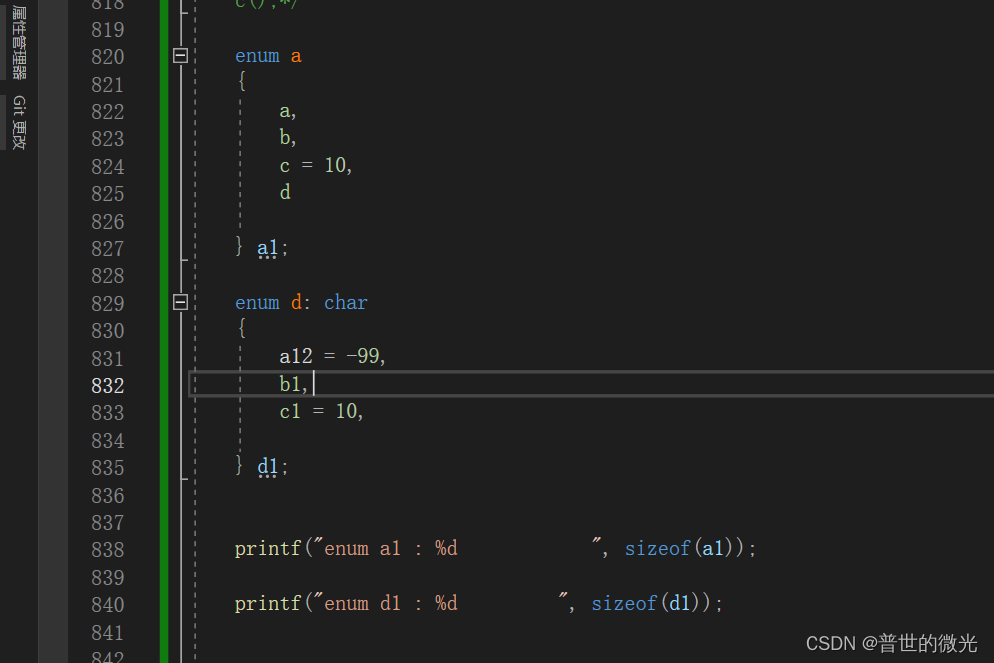
看到了吧 语法规则 和 struct 差不多
只不过枚举成员 只是一个标志
它本质是数值
从上到下 下面的数根据上面的数 加 1
也可以直接指定 数值
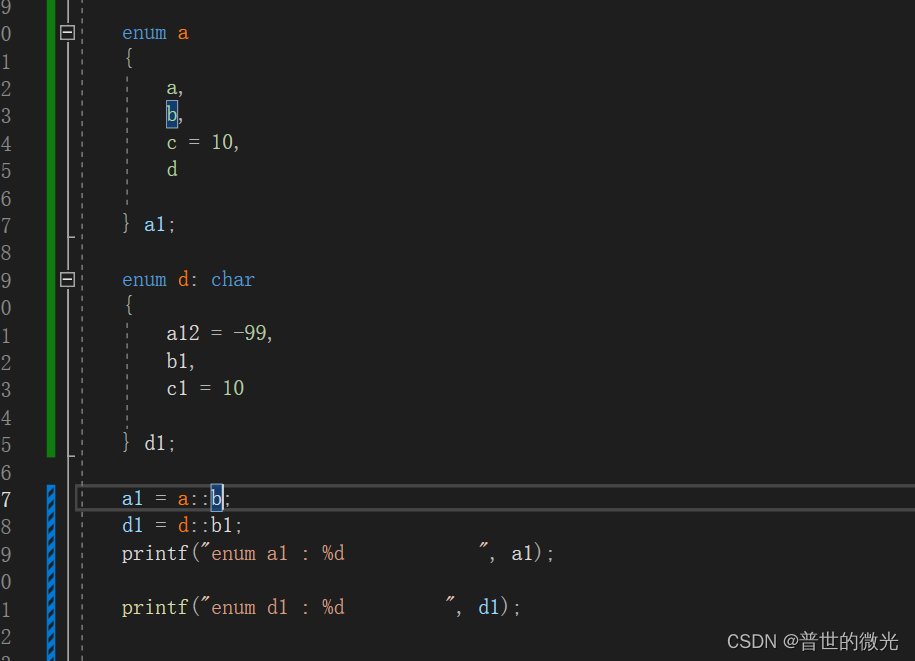

看下面的数 是上面数加1吧?
enum d: char
这个是什么?
有点像继承 但又不对
这个是什么 它可以指定枚举的内存使用的大小
我们知道枚举本质是数值 那么它的内存大小呢?

注意到没 一个是四字节 一个是一字节
至于为何叫无作用域
大概率是因为 内部成员没法重复的原因
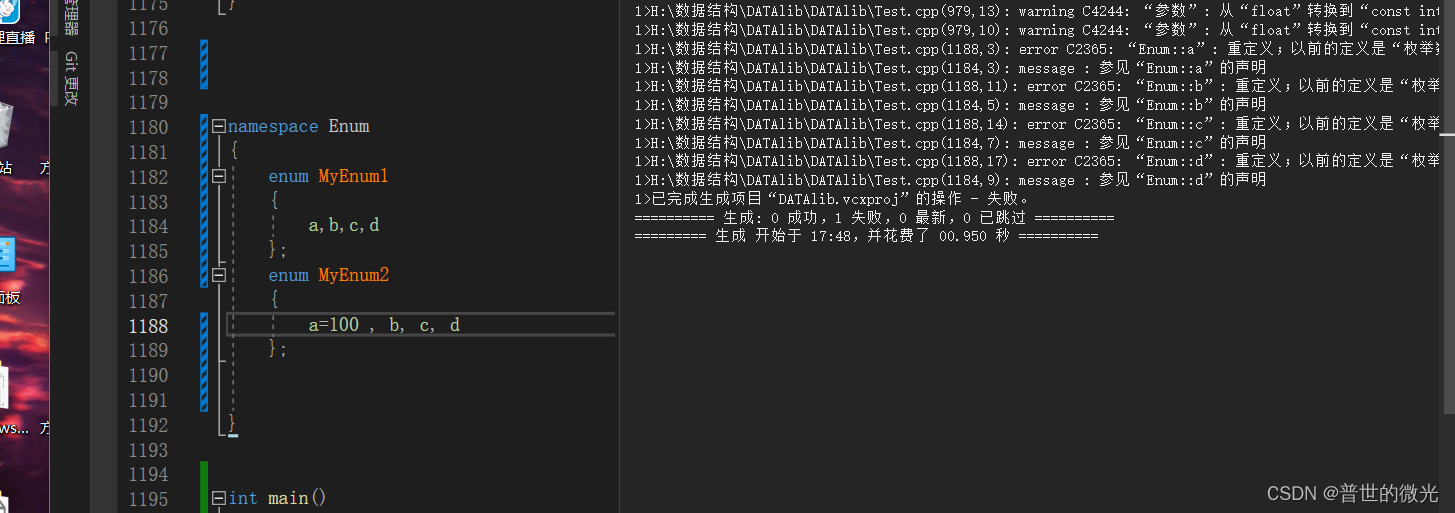
namespace Enum
{enum MyEnum1{a,b,c,d};enum MyEnum2{a=100 , b, c, d};}
这样是错误的编译没法过
原因就是因为 enum MyEnum1 enum MyEnum2
内部的 成员标志重复了
namespace Enum
{enum MyEnum1{q,w,e,r};}
enum MyEnum2
{q = 100, w, e, r
};这样可以隔绝在名称空间中
这样是允许的
你说这不合理 但规则就是如此
所以c++引入了enumclass / enumstruct 有作用域枚举
namespace Enum
{enum MyEnum1{q,w,e,r};}
enum MyEnum2
{q = 100, w, e, r
};enum class MyEnumClass1
{q,w,e,r};enum class MyEnumClass2
{q, w, e, r
};没有冲突
int main()
{MyEnumClass1 j;j = MyEnumClass1::q;Enum::MyEnum1 c = Enum::q;MyEnum2 k = q;int ki = k;//可以隐式转换//int ki1 = j;//不可以隐式转换int ki1 = static_cast<int>(j);//可以k = static_cast<MyEnum2>(101);return 0;
}我们来看看调用
MyEnum2 k = q;
注意这个没有?
无作用域枚举 定义以后可以直接访问到成员 仿佛是全局变量一般
MyEnum2 k = q;
int ki = k;//可以隐式转换
无作用域枚举 可以隐式转换到数值型
但是数值型不能隐式转换到 枚举类型 必须使用强制转换
k = static_cast<MyEnum2>(101);//MyEnum2::w
而有作用域枚举
访问必须使用作用域修饰符
MyEnumClass1 j;
j = MyEnumClass1::q;
不能隐式转换到数值型 需要使用强转
int ki1 = static_cast<int>(j);//可以
你会问 要是我用一个不存在于枚举里面的数 去强制转换为枚举会如何?
我也不知道 因为会直接等于 该值


)




- 第 4 章 UI状态的保存与恢复)




)
)
)



)
