今天我们接着来学习树上搜索（dfs深度优先搜索）

1.树的深度与子树大小

树的深度：规定根结点是树的第一层，树根的孩子结点是树的第二层，以此类推，树的深度就是结点的最大层数。

根据定义，如果我们已经知道树中某个结点 u 的深度 dep[u]，那么结点 
u 的儿子结点 
v 的深度 dep[v]=dep[u]+1。

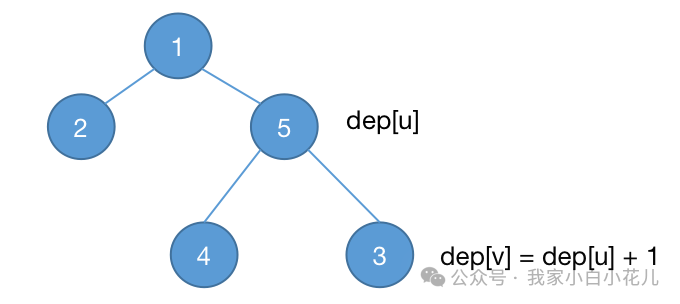
求解每个结点的深度：自上而下。

int dep[110];
void dfs(int u, int fa) {dep[u] = dep[fa] + 1;for (int i = 0; i < G[u].size(); i++) {int v = G[u][i];if (v != fa) {dfs(v, u);}}
}

在树上有一个很重要的概念是子树，子树就是包括当前节点和它底下所有节点的一棵树。

比如

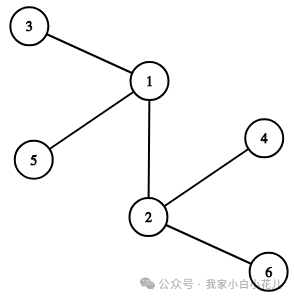
如果以 
1 为根，那么以 2 号结点为根的子树就包括 2,4,6 三个点，这棵子树大小就是 3 。

这一节我们就来求解以每个点为根的子树的大小。

解决子树问题，往往是把一棵子树拆成子树的根和底下的很多棵小的子树。

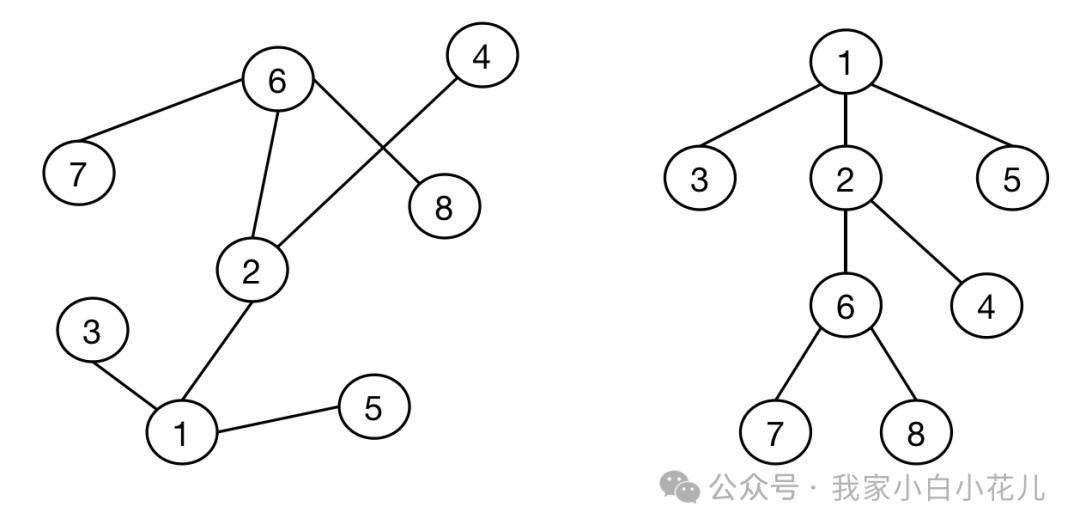
比如这里，如果 
1 是整棵树的根，那么以 2 为根的子树，可以拆成 2 （子树根），6,7,8（以 6 为根的子树），4（以 4 为根的子树），三部分，这三部分的点数加起来就是这棵子树的大小。

所以一个子树可以拆成子树根（一个节点）和每一棵以它的孩子为根的子树，所以这棵子树的大小就是所有以它的孩子为根的子树的大小的和再加 1。

接下来我们来研究如何通过代码解决这样的问题，对于当前节点来讲我们需要让它先搜索它的所有子节点，得到这些子节点的子树的大小，加起来再加 11 。

首先我们需要一个数组sz记录以每个点为根的子树的大小。

然后我们可以把搜索的dfs函数返回值改为int类型，返回以当前节点u为根的子树的大小。这样我们在找每一个与当前节点u相连的子节点v的时候，把到v去搜索得到的返回值加进sz[u]上，这样就把以u的每个子节点为根的子树的大小都加进来了，最后再给sz[u]加上 11（u节点本身），返回就可以了。

代码就是这样

​​​​​​​
int sz[110];
int dfs(int u, int fa) {for (int i = 0; i < G[u].size(); i++) {int v = G[u][i];if (v != fa) {sz[u] += dfs(v, u);}}sz[u]++;return sz[u];
}

求解每棵子树的大小：自下而上。

如果大家把搜索过程画出来，把dfs序写出来会发现，一棵子树一定是在dfs序上一段连续的序列，这一点是dfs序一个非常好的性质，也是dfs序最有用的性质。

比如

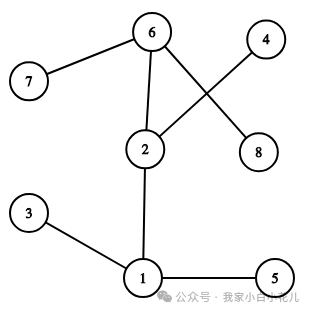
这棵树，以 1 为根，一种dfs序就是 1,2,6,7,8,4,3,5 ，会发现以每个点为根的子树都对应了这个dfs序的连续一段。

这个也是因为dfs本身就需要把当前点以下的所有点都搜完了才会返回到上一层的点。