【2024美赛C题】网球大佬带你无背景压力分析解题思路！

2024美赛数学建模c题思路分享

加群可以享受定制等更多服务，或者搜索B站：数模洛凌寺

联络组织企鹅：936670395

以下是C题老师的解题思路（企鹅内还会随时更新文档）：

1背景介绍

2024MCM问题C：网球运动中的势头
在这里插入图片描述

在2023年温布尔登网球公开赛男子组决赛中，20岁的西班牙新星卡洛斯-阿尔卡拉斯击败了36岁的诺瓦克-德约科维奇。这是德约科维奇自2013年以来首次在温布尔登输掉比赛，也结束了这位大满贯历史上最伟大球员之一的辉煌战绩。
[1]德约科维奇似乎注定会轻松获胜，他在第一盘以6-1的比分占据优势（7局比赛中赢了6局）。然而，第二盘比赛却十分紧张，最终阿尔卡雷斯在决胜盘中以7-6获胜。第三盘与第一盘相反，阿尔卡拉兹以6-1的比分轻松获胜。第四盘开始后，年轻的西班牙人似乎完全控制了局面，但不知何故，比赛的走势再次发生了变化，德约科维奇完全控制了局面，以6-3的比分赢得了这一盘。第五盘也是最后一盘比赛开始后，德约科维奇延续了第四盘的优势，但比赛的走向再次发生了变化，阿尔卡拉斯以6-4取得了胜利。本场比赛的数据在提供的数据集中，“match_id"为"2023-wimbledon-1701”。您可以使用"set_no"列（等于1）查看第一盘德约科维奇占优时的所有得分。似乎占优的一方有时会出现多分甚至多局的惊人波动，这通常归因于"势头"。
在字典中，“势头"的定义是"通过运动或一系列事件获得的力量或作用力。”[2]在体育运动中，一支球队或一名球员可能会觉得他们在比赛中拥有势头或"力量/作用力"，但很难衡量这种现象。此外，如果存在"势"的话，比赛中的各种事件是如何产生或改变"势"的，也不是一目了然的。
提供2023年温布尔登网球公开赛前两轮之后所有男子比赛中每一分的数据。您可以自行决定加入其他球员信息或其他数据，但必须完整记录数据来源。使用这些数据
（1）建立一个模型，捕捉赛点发生时的比赛流程，并将其应用到一场或多场比赛中。您的模型应能确定哪位球员在比赛中的某个特定时间段表现更好，以及他们的表现好到什么程度。根据您的模型提供可视化的比赛流程描述。注意：在网球比赛中，发球的一方赢得赛点/比赛的概率要高得多。您可能希望以某种方式将这一因素考虑到您的模型中。
（2）一位网球教练对"势头"在比赛中的作用持怀疑态度。相反，他假设比赛中的波动和一名球员的成功是随机的。请使用您的模型/度量来评估这一说法。
（3）练们很想知道，是否有一些指标可以帮助判断比赛的流程何时会从偏向一名球员变为偏向另一名球员。
（4）利用提供的至少一场比赛的数据，建立一个模型来预测比赛中的这些波动。哪些因素似乎最相关（如果有的话）？
（5）考虑到过去比赛"势头"波动的差异，您如何建议球员在新的比赛中对阵不同的球员？
（6）在一场或多场其他比赛中测试您开发的模型。您对比赛中的波动预测得如何？
如果模型有时表现不佳，您是否能找出未来模型中可能需要包含的任何因素？您的模型对其他比赛（如女子比赛）、锦标赛、球场表面和其他运动（如乒乓球）的通用性如何？
（7）撰写一份不超过25页的报告，介绍您的研究结果，并附上一至两页的备忘录总结您的研究结果，并就"动力"的作用以及如何让球员做好准备，应对网球比赛中影响比赛进程的事件，向教练提出建议。

2 问题重述

本题详细描述了2023年温布尔登网球公开赛男子组决赛的比赛情况以及提供的比赛数据。要求解释了"势头"在体育运动中的定义以及难以衡量的问题。并解决以下的几个问题：

（1）建立一个模型，包括：

1.捕捉网球赛点发生时的比赛流程的模型。
2.应用到一场或多场比赛中以确定表现更好的球员，并提供可视化描述。
（2）对"势头"作用的，使用模型/度量来评估。
（3）探讨一些指标，用于判断比赛流程何时会从偏向一名球员变为偏向另一名球员。
（4）利用提供的比赛数据，建立一个波动预测模型，并确定最相关的因素。
（5）提出如何建议球员在新的比赛中对阵不同的球员，考虑到过去比赛"势头"波动的差异。
（6）在一场或多场其他比赛中测试开发的模型，并评估模型的波动预测。
（7）撰写报告和备忘录，介绍研究结果并向教练提出建议。

3 问题初步分析

3.1 问题一：捕捉赛点发生时的比赛流程的模型

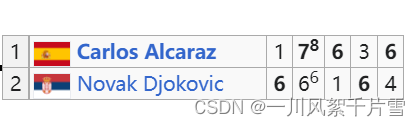
在这里插入图片描述

2023温网决赛数据
（1）模型思路：这是一个时间序列预测回归问题。将赛点发生时的比赛情况建模为状态转移过程，根据历史比赛数据和技术统计来预测赛点的发生。由于计分的模型是按每一盘、每一局计分的，大满贯的需要打5盘3胜出，每一盘是赢6局，或者6：6时，一局定胜负，这一局是先抢到7分的胜出，如果6：6时，需要再净胜出2分才能赢下这一局。在数据预处理部分，可以将前面的赢下的盘作为一个特征，如果前4盘中已经赢下2盘，则直接预测第三盘是否会出现赛点。并且由于将计分转为一条时间序列的数据，可以将计分数据转换为事件数据，例如记录每一个赛点的发生情况，赛点发生时双方的计分情况，以及赛点赢家等。之后用时间序列回归模型预测即可，以下给出示例代码。
（2） 模型
●马尔可夫链模型（Markov Chain Model）: 将比赛状态建模为马尔可夫链，推断赛点发生的概率。
隐马尔可夫模型（Hidden Markov Model）: 考虑比赛状态的隐含变量，对赛点的发生进行建模。
●逻辑回归模型（Logistic Regression）: 根据选手的技术统计特征，预测赛点的可能性。
生存分析模型（Survival Analysis）: 考虑赛点发生的时间，建立生存分析模型来预测赛点的发生。
●朴素贝叶斯模型（Naive Bayes）: 基于历史数据和技术统计，利用贝叶斯方法预测赛点的发生。
要将网球大满贯中5盘的计分数据转换为一条时间序列的数据，可以将每个赛点的计分情况转换为时间序列中的事件，然后使用这些事件数据来建立时间序列模型，例如隐马尔可夫模型或马尔可夫链模型，来预测赛点的发生。下面是举例理解Python代码：
（3）示例：举例的5盘比赛的计分数据

import pandas as pd#假设我们有原始的比分数据，包括每局的比分情况
#这里的具体每一局的分数，是我瞎编的，需要根据提供的表格计算得出准确值，后续我会更新正确。
score_data = {'Set1': ['4-1', '1-4', '4-2', '4-0', '4-0', '4-3', '4-2'],# 第一盘，打了7局，6：1'Set2': ['4-1', '1-4', '4-2', '4-0', '4-0', '4-3', '4-2', '1-4', '4-2', '4-0', '4-0', '4-3', '4-2'],# 第二盘，打了13局，7：6'Set3': ['4-1', '1-4', '4-2', '4-0', '4-0', '4-3', '4-2'],# 第三盘，打了7局，6：1'Set4': ['4-1', '1-4', '4-2', '4-0', '4-0', '4-3', '4-2','4-3', '4-2'],# 第四盘，打了9局，3：6'Set5': ['4-3', '4-2','4-1', '1-4', '4-2', '4-0', '4-0', '4-3', '4-2','4-3'] # 第五盘，打了10局，4：6
}#转换成时间序列的事件数据
events = []
for set_num in score_data:set_scores = score_data[set_num]for game_score in set_scores:# 分割比分player1, player2 = game_score.split('-')player1 = int(player1)player2 = int(player2)# 判断赛点情况if player1 >= 4 and player1 - player2 >= 2:events.append({'set': set_num, 'game': game_score, 'player': 'Alcaraz', 'event': '赛点'})elif player2 >= 4 and player2 - player1 >= 2:events.append({'set': set_num, 'game': game_score, 'player': 'Djokovic', 'event': '赛点'})#转换为DataFrame
events_df = pd.DataFrame(events)#打印事件数据
print(events_df)

上述代码将原始计分数据转换为了赛点事件的时间序列数据。然后可以使用events_df进行时间序列建模，例如应用隐马尔可夫模型：

from hmmlearn import hmm#建立隐马尔可夫模型
model = hmm.GaussianHMM(n_components=2, covariance_type="full")
X = events_df[['set', 'game']]  # 选择用于建模的特征
model.fit(X)#进行赛点预测
predicted_states = model.predict(X)#打印预测结果
print(predicted_states)

3.2 问题二：评估"势头"作用的模型

（1）模型思路：这是一个因子分析问题，通过统计和机器学习方法，评估球员的赛事表现是否受到"势头"的影响，探索势头效应的存在和程度。
（2） 模型
●线性回归模型（Linear Regression）：分析球员的比赛表现与势头的相关性，探索线性关系。
时间序列模型（Time Series Model）：分析球员的比赛结果时间序列，检测势头效应的存在和影响。
●因子分析（Factor Analysis）：挖掘比赛数据中的潜在因子，探索势头对表现的影响。
贝叶斯结构学习（Bayesian Structural Learning）：利用贝叶斯方法建立模型，评估势头作用的概率和影响。
●强化学习模型（Reinforcement Learning）：通过建立马尔可夫决策过程模型来评估势头对球员战术选择的影响。

3.3 问题三： 判断比赛流程转向的指标

（1）模型思路：这是一个分类问题，是球员A赢下的概率大，还是球员B的概率大。建立状态转移模型来判断比赛流程何时转向另一名球员，考虑技术统计和比分变化。
（2） 模型：
●隐马尔可夫模型（Hidden Markov Model）：考虑比赛状态的隐含变量，判断比赛流程的转向。
KNN模型（K-Nearest Neighbors）：根据历史数据中邻近的比赛情况来判断比赛流程的转向。
●决策树模型（Decision Tree）：利用技术统计特征来建立决策树模型，判断比赛流程的转向。
时间序列分析模型（Time Series Analysis）：分析比赛数据的时间序列特征，判断比赛流程转向的规律。
●支持向量机模型（Support Vector Machine）：根据技术统计特征，建立支持向量机模型来判断比赛流程的转向。

3.4 问题四： 建立波动预测模型

（1）模型思路：这是时间序列预测问题，将问题一的数学模型拿来用就行，做一些漂亮的回归分析和可视化。利用比赛数据和技术统计，建立波动预测模型来确定比赛结果的波动，并找出最相关的因素。
（2）模型：
●时间序列模型（Time Series Model）：建立时间序列预测模型，预测比赛结果的波动。
●ARIMA模型：利用自回归与移动平均模型，预测比赛结果的波动情况。
●LSTM模型（Long Short-Term Memory）：利用循环神经网络模型来预测比赛结果的波动。
●随机森林模型（Random Forest）：利用多颗决策树组成的模型来预测比赛结果的波动。
●因果推断模型（Causal Inference Model）：利用因果推断方法来确定比赛结果波动的因果关系。

3.5 问题五：战术建议

（1）建议思路：这是一个决策问题，通过比较对阵不同对手时的比赛"势头"波动差异，给出针对不同对手的战术建议，简答一点做就是用决策树做，要做复杂点就加入博弈论的思想，方法更高级。
（2）模型
●博弈论模型（Game Theory）：分析不同对手之间的博弈关系，给出对应的战术建议。
强化学习模型（Reinforcement Learning）：通过与不同对手的交互学习，给出对应的战术建议。
●决策树模型（Decision Tree）：根据对手的特点建立决策树模型，给出相应的战术建议。
概率图模型（Probabilistic Graphical Model）：利用概率图模型分析不同对手的特点，给出对应的战术建议。

3.6 问题六：模型评估

以上几乎都是回归问题，回归问题的模型评价方法部分举例如下：
●交叉验证（Cross-validation）：对模型在其他比赛中的表现进行交叉验证，评估模型的波动预测能力。
●均方误差（Mean Squared Error）：计算模型在其他比赛中的均方误差，评估模型的预测准确性。
●ROC曲线分析（ROC Curve Analysis）：通过绘制ROC曲线，评估模型的波动预测性能。
●查准率与召回率（Precision and Recall）：计算模型的查准率与召回率，评估模型的波动预测能力。
●AUC值评估（AUC Value Evaluation）：计算模型的AUC值，评估模型的波动预测性能。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/662080.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

LeetCode：42. 接雨水

LeetCode：42. 接雨水

42. 接雨水 1）题目2）思路3）代码4）结果 1）题目 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。 示例 1： 输入：height …
阅读更多...
强化学习 - Monte Carlo Tree Search (MCTS)

强化学习 - Monte Carlo Tree Search (MCTS)

什么是机器学习 强化学习中的Monte Carlo Tree Search (MCTS) 是一种用于决策制定和搜索的算法，特别在不确定环境下表现出色。 1. 强化学习背景 在强化学习中，一个智能体通过与环境的交互学习，以便在某个任务上获得最大的奖励。MCTS是一种…
阅读更多...
2024美国大学生数学建模美赛选题建议+初步分析

2024美国大学生数学建模美赛选题建议+初步分析

总的来说&#xff0c;去年算是美赛环境题元年&#xff0c;去年的开放度是较高的&#xff0c;今年每种赛题类型相对而言平均了起来 提示&#xff1a;DS C君认为的难度&#xff1a;E<BCF<AD&#xff0c;开放度&#xff1a;DBCE<A<F。 以下为A-F题选题建议及初步分析…
阅读更多...
【ArcGIS Pro】从0开始

【ArcGIS Pro】从0开始

1.导入excel&#xff0c;需要安装驱动程序 安装用于 Microsoft Excel 文件的驱动程序 https://pro.arcgis.com/zh-cn/pro-app/latest/help/data/excel/prepare-to-work-with-excel-in-arcgis-pro.htm 2.修改投影坐标系 点到地图图标上&#xff0c;右键才能设置坐标系。 3.…
阅读更多...
前端通过nginx,访问一个文件夹里面的全部数据，nginx 咋配置

前端通过nginx,访问一个文件夹里面的全部数据，nginx 咋配置

目录 1 问题2 实现 1 问题 前端通过nginx,访问一个文件夹里面的全部数据&#xff0c;nginx 咋配置 2 实现 location /logs {alias /mnt/www/logs/;autoindex on; }
阅读更多...
【QT+QGIS跨平台编译】之二十二：【FontConfig+Qt跨平台编译】（一套代码、一套框架，跨平台编译）

【QT+QGIS跨平台编译】之二十二：【FontConfig+Qt跨平台编译】（一套代码、一套框架，跨平台编译）

文章目录 一、FontConfig介绍二、文件下载三、文件分析四、pro文件五、编译实践 一、FontConfig介绍 FontConfig 是一个用于配置和定制字体的库&#xff0c;广泛应用于基于X Window系统的操作系统中&#xff0c;尤其是在Linux和Unix-like系统中。它为应用程序提供了一种统一的…
阅读更多...
JavaWeb前端——HTML/CSS

JavaWeb前端——HTML/CSS

HTML/CSS概述 HTML&#xff1a;学习标签&#xff0c;CSS&#xff1a;学习样式 HTML 1. 不区分大小写。 2. 属性可以使用单引号/双引号 3. 在记事本/编辑器中编写html语言&#xff0c;通过浏览器解析渲染语言 4. 语法结构松散&#xff08;编写时要尽量严谨&#xff09; VSc…
阅读更多...
搭建 idea 插件仓库私服

搭建 idea 插件仓库私服

正常情况下&#xff0c;我们开发的 idea 插件会发布到 idea 官方商城中&#xff0c;这样用户就可以在 idea 的 Marketplace 中搜索安装。 但是在企业内部&#xff0c;有可能我们开发了很多内部插件&#xff0c;而不能发布到公共市场中&#xff0c;这种情况下我们就需要搭建一个…
阅读更多...
探索微服务治理：从发展到实践构建高效稳定的系统｜负载均衡技术解析

探索微服务治理：从发展到实践构建高效稳定的系统｜负载均衡技术解析

二、微服务治理的相关技术 微服务治理涉及多个方面&#xff0c;包括服务注册与发现、负载均衡、容错处理、服务配置管理等&#xff0c;这些技术共同确保微服务架构的稳定运行。 2、负载均衡 负载均衡作为服务治理中的核心技术之一&#xff0c;对于提高系统的可用性、性能和扩…
阅读更多...
网络空间测绘在安全领域的应用（上）

网络空间测绘在安全领域的应用（上）

近年来&#xff0c;网络空间测绘已经跻身为网络通信技术、网络空间安全、地理学等多学科融合的前沿领域。 该领域聚焦于构建网络空间信息的“全息地图”&#xff0c;致力于建立面向全球网络的实时观测、准确采样、映射和预测的强大基础设施。 通过采用网络探测、数据采集、信…
阅读更多...
华为FreeClip耳机可以调节音量大小吗？附教程！

华为FreeClip耳机可以调节音量大小吗？附教程！

不会只有我一个人吧&#xff1f;都用华为FreeClip耳机一段时间了&#xff0c;才发现它竟然不支持在耳机上直接调节音量&#xff0c;也是没谁了&#xff01;但是后来自己摸索了一下&#xff0c;发现了华为FreeClip耳机原来是几个简单有效的调节音量大小的方法滴~不得不说&#x…
阅读更多...
在Android Studio中配置OpenCV

在Android Studio中配置OpenCV

在Android Studio中配置OpenCV 1 下载OpenCV2 导入OpenCV模块3 修改配置4 增加依赖5 拷贝libopencv_java.so6 Activity中加入代码1 下载OpenCV 下载OpenCV的Android包并解压。 2 导入OpenCV模块 在Android应用中，导入OpenCV模块。 导入目录时选择Opencv Android中的sdk目…
阅读更多...
TiDB架构设计和实践：高性能分布式数据库解决方案

TiDB架构设计和实践：高性能分布式数据库解决方案

摘要&#xff1a;TiDB是一个开源的分布式NewSQL数据库&#xff0c;具备强大的水平扩展能力和高性能查询能力。本文将介绍TiDB的架构设计和实践经验&#xff0c;帮助读者了解如何利用TiDB构建可靠、高性能的分布式数据库系统。 正文&#xff1a; ### 1. 引言 随着互联网规模的…
阅读更多...
鸿蒙ArkUI下拉列表组件

鸿蒙ArkUI下拉列表组件

鸿蒙ArkUI下拉列表组件&#xff0c;官方提供的只是基础使用&#xff0c;在使用过程非常不方便&#xff0c;我们进行了组件的封装。 import {IDynamicObject} from ./IType /*** 自定义颜色*/ Component export default struct DiygwSelect{//绑定的值Link Watch(onValue) val…
阅读更多...
如何做好员工离职风险防范和离职危机处理工作

如何做好员工离职风险防范和离职危机处理工作

员工退出与离职是企业发展中都会面临的一个普遍现象&#xff0c;这种现象本身没有什么问题&#xff0c;但是如果企业退出与离职管理不善&#xff0c;就会增加企业的管理成本&#xff0c;影响企业的正常经营活动。该电子科技有限公司在发展中也遇到员工离职管理不善带来的问题。…
阅读更多...
151基于matlab的齿轮-轴-轴承系统的含间隙非线性动力学模型

151基于matlab的齿轮-轴-轴承系统的含间隙非线性动力学模型

基于matlab的齿轮-轴-轴承系统的含间隙非线性动力学模型&#xff0c;根据牛顿第二定律&#xff0c;建立齿轮系统啮合的非线性动力学方程&#xff0c;同时也主要应用修正Capone模型的滑动轴承无量纲化雷诺方程&#xff0c;利用这些方程推到公式建模&#xff1b;用MATLAB求解画出…
阅读更多...
查看docker服务的IP地址

查看docker服务的IP地址

要查看Docker容器服务的IP地址&#xff0c;可以使用以下命令&#xff1a; 如果你知道容器名称或容器ID&#xff0c;直接通过容器ID或容器名称来获取IP地址&#xff1a; # 使用容器ID获取IP地址 docker inspect -f {{range .NetworkSettings.Networks}}{{.IPAddress}}{{end}} …
阅读更多...
jupyter notebook显示的扩展很少，只有四五个--解决方案

jupyter notebook显示的扩展很少，只有四五个--解决方案

如下&#xff1a;安装好只有四五个扩展 可以先删除 conda remove jupyter_nbextensions_configurator 然后使用pip安装 pip install jupyter_contrib_nbextensions jupyter contrib nbextensions install --user pip install jupyter_nbextensions_configurator jupyter nbex…
阅读更多...
c++学习第十四讲---STL常用容器---vector容器

c++学习第十四讲---STL常用容器---vector容器

vector容器&#xff1a; 1.vector基本概念&#xff1a; vector功能与数组类似&#xff0c;与数组不同的是&#xff0c;vector可以动态扩展。 2.vector构造函数&#xff1a; vector<T> v; //默认构造函数&#xff0c;创建数据类型T的容器 ve…
阅读更多...
JAVA操作Rabbitmq-原理讲的很详细

JAVA操作Rabbitmq-原理讲的很详细

这篇文章来源于稀土掘金&#xff0c;来源&#xff1a;https://juejin.cn/post/7132268340541653005&#xff0c;主要用来收藏学习。 常见的消息队列很多&#xff0c;主要包括 RabbitMQ、Kafka、RocketMQ 和 ActiveMQ&#xff0c;相关的选型可以看我之前的系列&#xff0c;这篇文…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023