欢迎来到《小5讲堂》，大家好，我是全栈小5。
这是《Docker容器》系列文章，每篇文章将以博主理解的角度展开讲解，
特别是针对知识点的概念进行叙说，大部分文章将会对这些概念进行实际例子验证，以此达到加深对知识点的理解和掌握。
温馨提示：博主能力有限，理解水平有限，若有不对之处望指正！

前言

前一篇文章已经在Docker Desktop管理工具尝试添加Docker Nginx容器，也成功访问到前端页面。
本篇文章将在Docker下部署.net core项目，并访问core项目下的接口返回数据。

创建项目

创建新项目

博主这里选择的是ASP.NET Core Web API，指名项目只支持api接口，已经是完全前后端分离的思想框架。

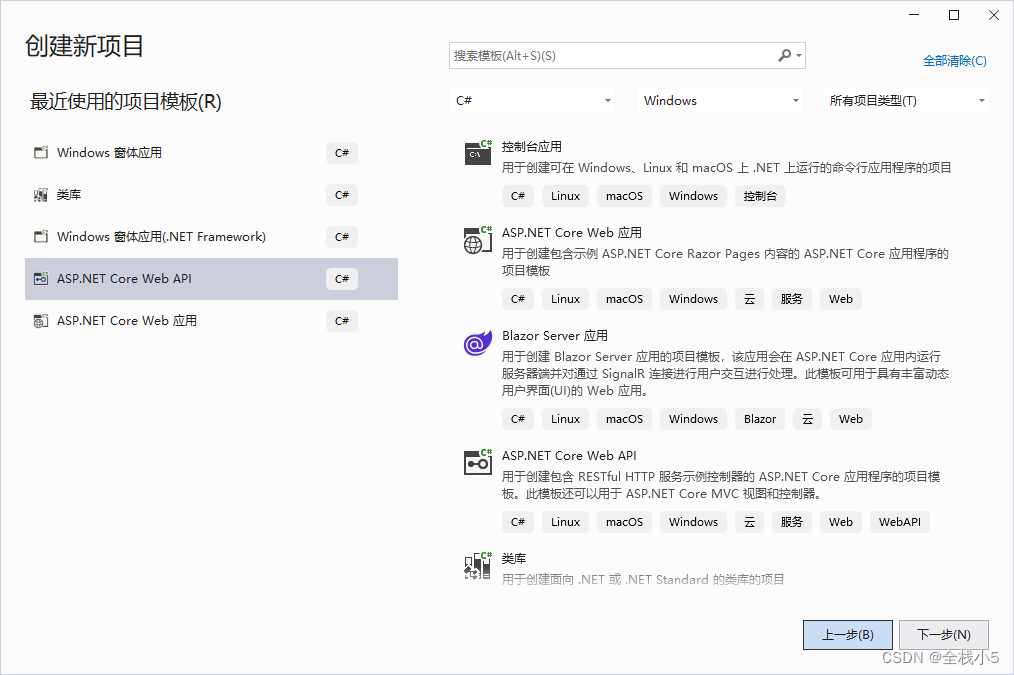
配置新项目

主要填写项目名称、项目存放位置路径，解决方案和项目是否放在同一目录

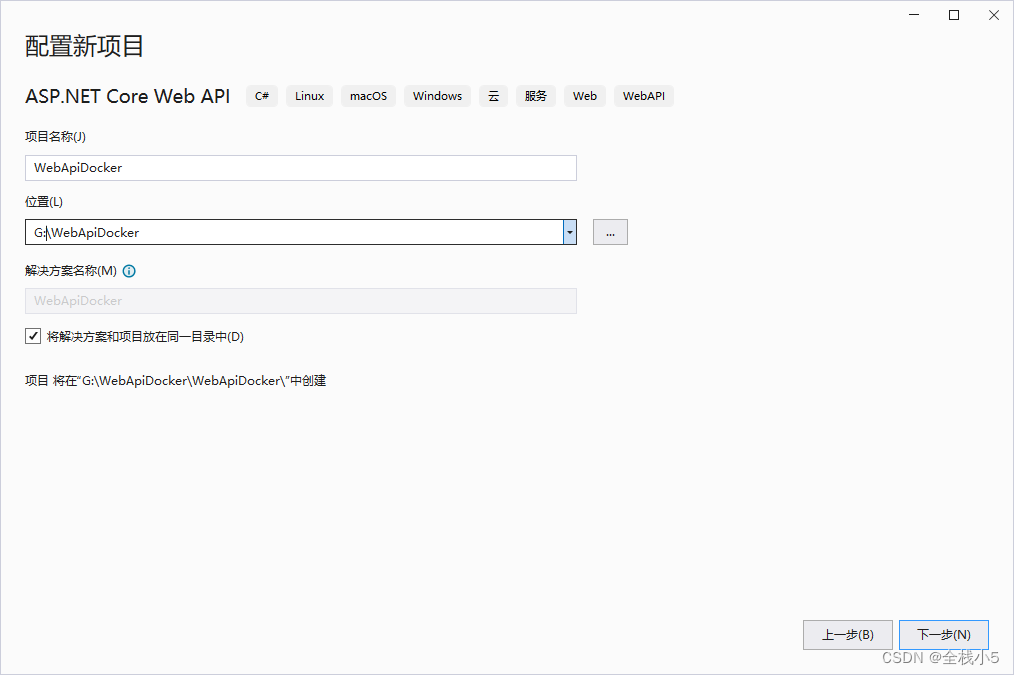
• 在同一目录
  
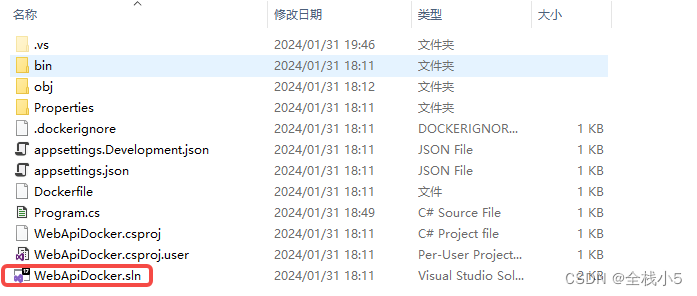
• 不在同一目录
  

启动Docker

博主这里选择的是.NET 6.0（支持.net framework和.net core），并且启用Docker，并且Docker OS选择Linux

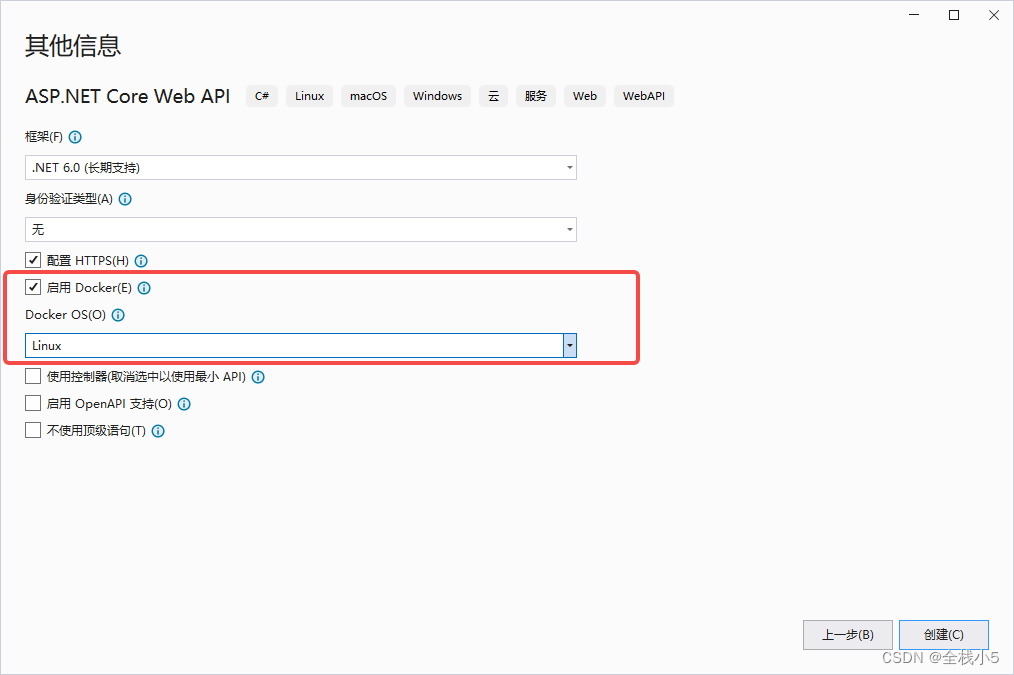
项目结构

完成上面步骤选择后，下面是默认项目结构，在项目文件夹下是由Dockerfile文件，比如：可以设置防止乱码之类的参数

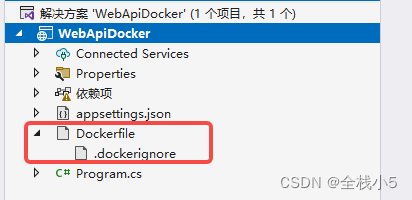
Dockerfile 是在使用 Docker 构建容器镜像时使用的文本文件。
它包含一系列指令和参数，用于定义如何构建镜像以及运行容器的配置。
在 VS (.NET Core) 开发中，Dockerfile 通常用于构建和部署 .NET Core 应用程序的容器镜像。
它提供了一种可重复、可管理的方式来定义所需的软件环境、依赖项和运行时配置。
通过 Dockerfile，可以指定基础镜像、添加应用程序代码、安装所需的库和工具、设置环境变量、指定工作目录和端口暴露等步骤。
一旦 Dockerfile 定义完成，可以使用 Docker 命令来构建镜像，然后使用该镜像创建和运行容器，从而轻松地在不同的环境中部署和运行 .NET Core 应用程序。

Dockerfile 的作用是提供了一种可重复、可扩展和可移植的方式来构建和配置容器镜像。
它使得开发人员可以更轻松地管理应用程序的依赖和运行时环境，并能够在不同的开发、测试和生产环境中保持一致的部署体验。
此外，使用 Dockerfile 还可以实现自动化构建和持续集成/交付 (CI/CD) 流程，加快应用程序的开发和发布速度。

启动项目

首次启动

VS直接F5启动运行项目后，第一次会自动生成了2个容器（这个是因为Dockerfile有相关参数设置或者系统识别）

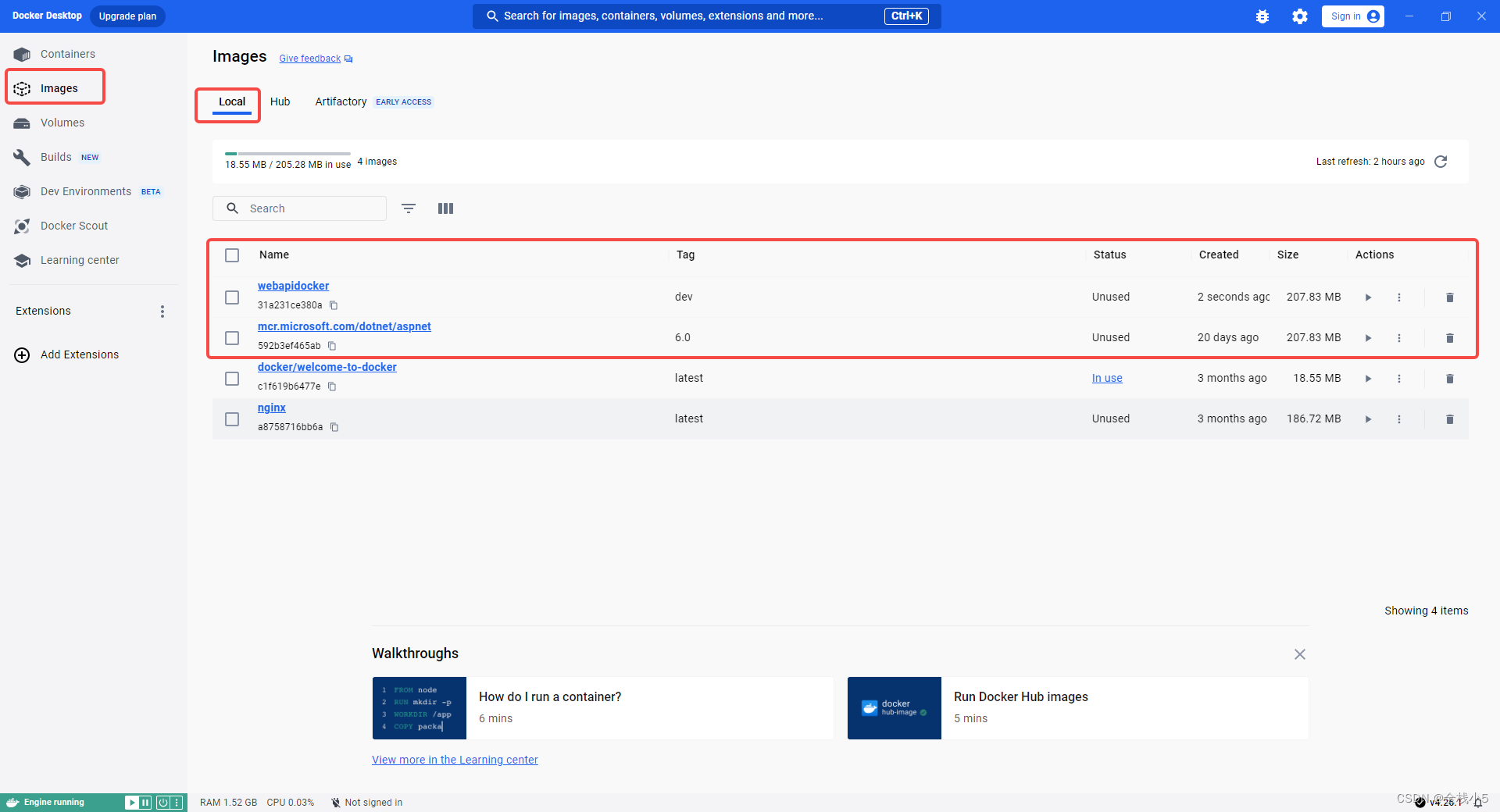
二次启动

出现下面这个提示，多次下一步后运行第二次

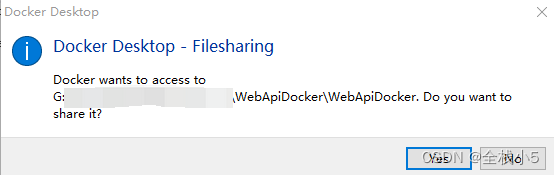
第二次运行和第一次有点不同，少了一个容器，只有主项目名称一致全小写的容器

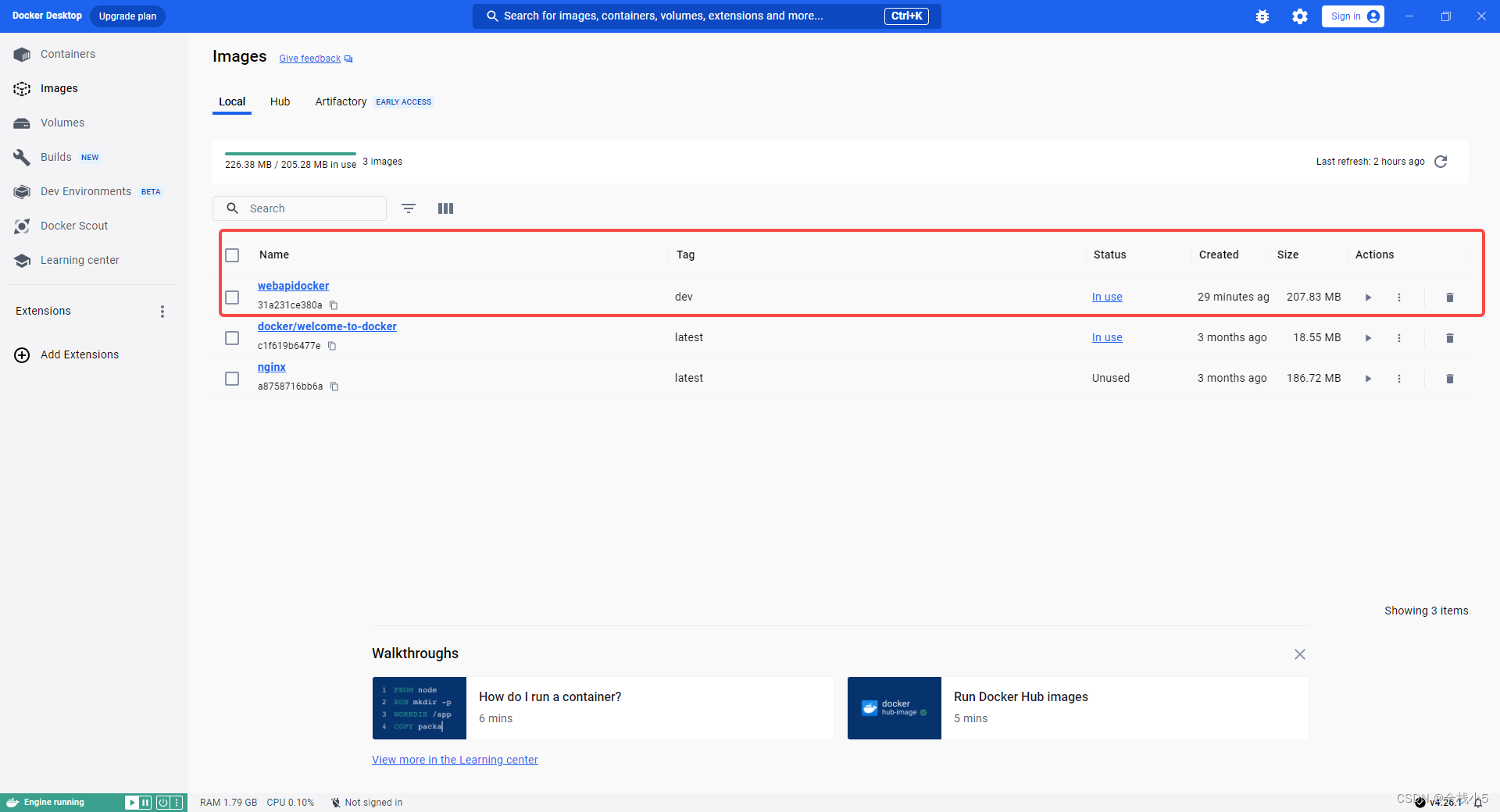
运行容器

在自动创建好的容器镜像列表，点击Action按钮，会弹出一个配置端口等信息窗口，保存后就会在容器列表有一条记录，点击端口会跳转到浏览器页面

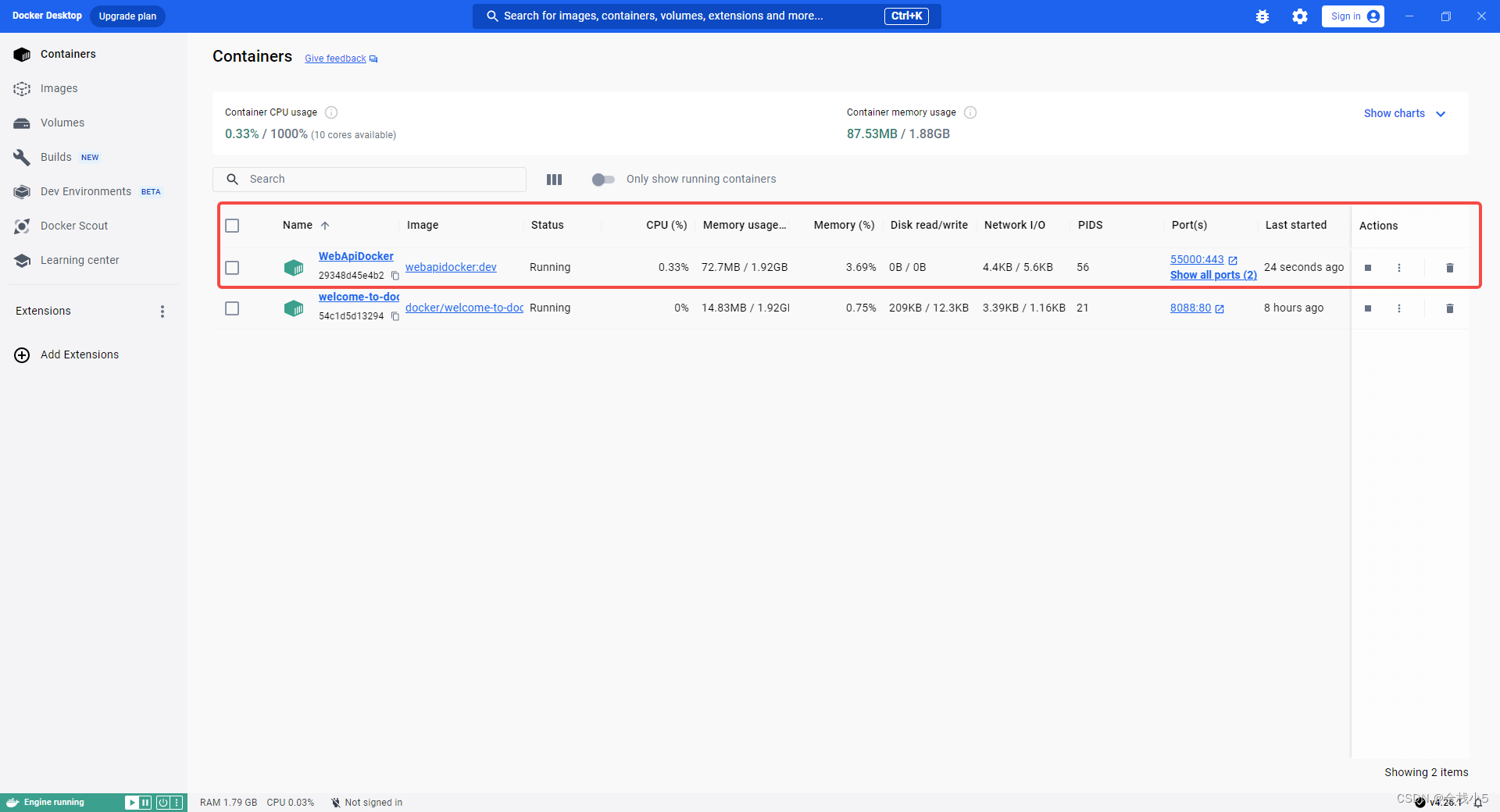
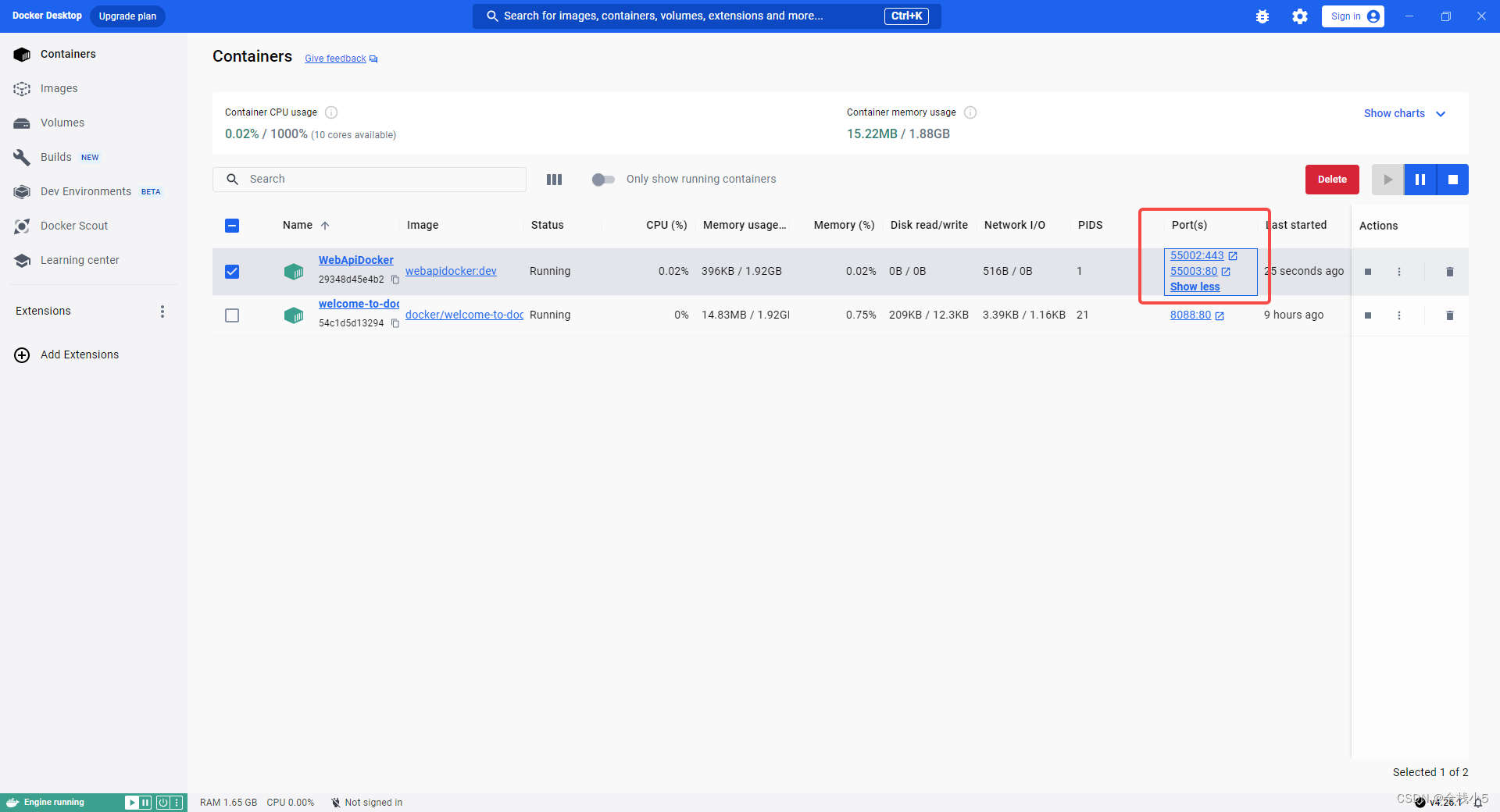
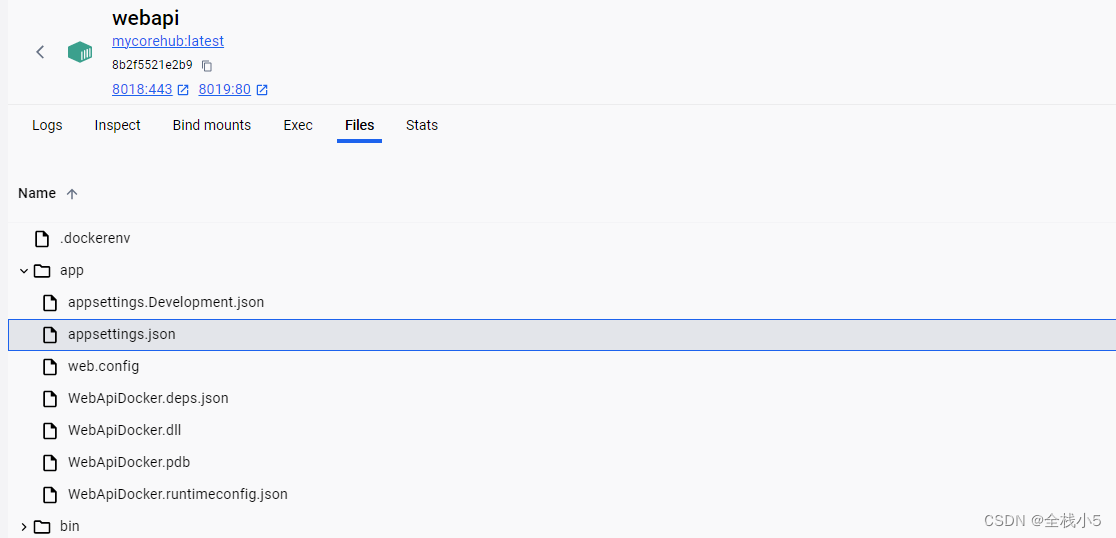
访问效果

跳转到浏览器页面，可以看到返回了接口api数据

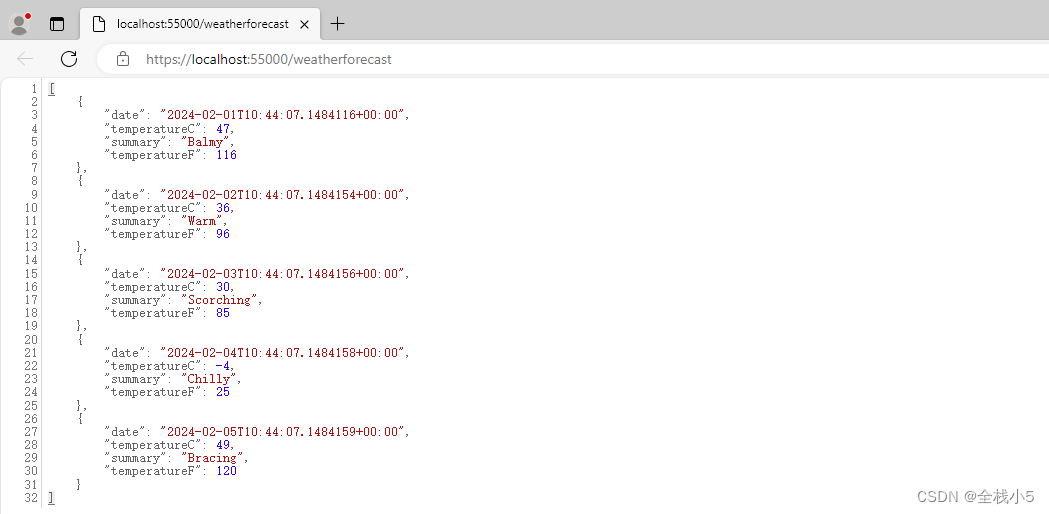
增加API接口

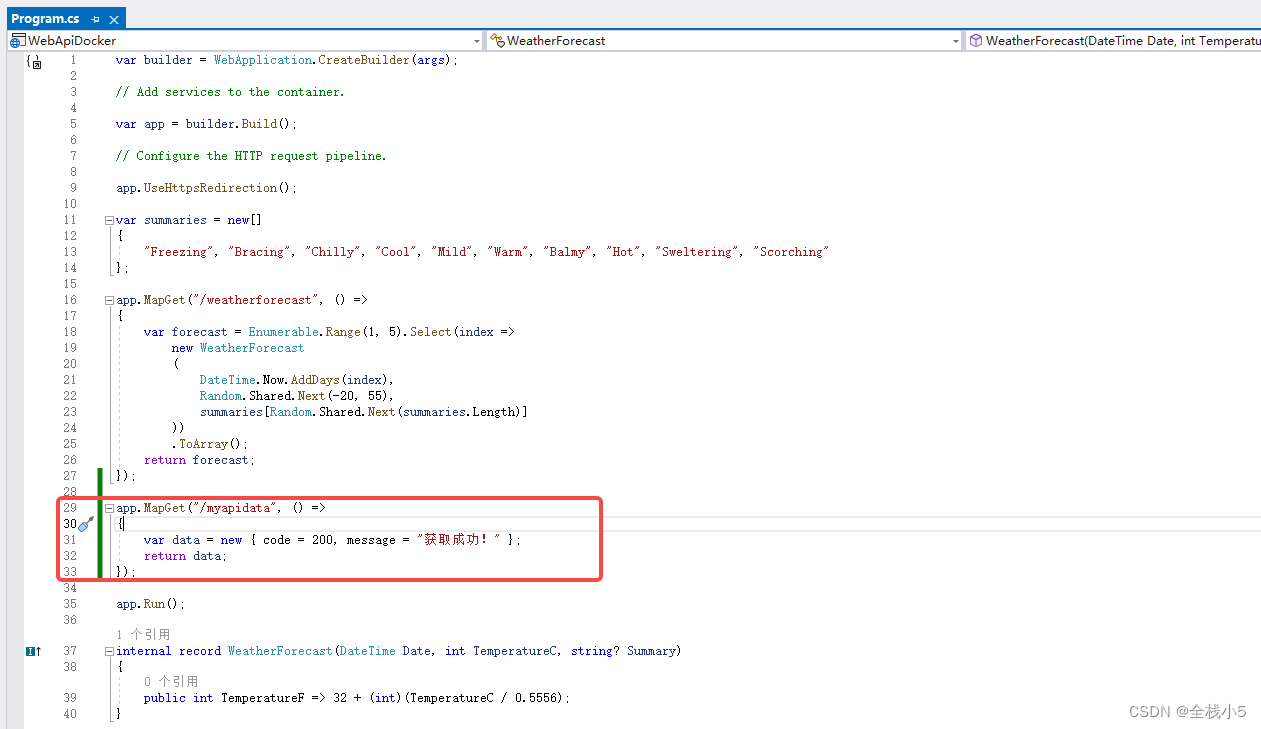
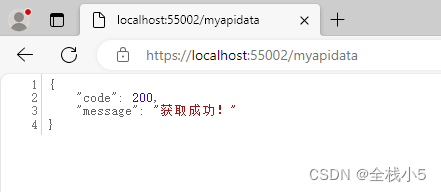
打包部署

上面是通过运气启动的容器，若停止VS调试运行，则访问会失效，因此可以通过打包部署到docker容器里，然后在单独容器里启动

项目打包

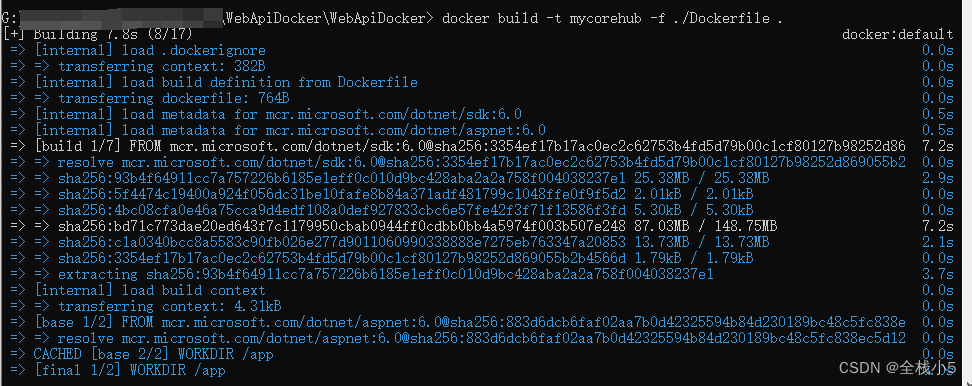
cmd命令：docker build -t mycorehub -f ./Dockerfile .
定位到具体目录：cd /d 自己路径

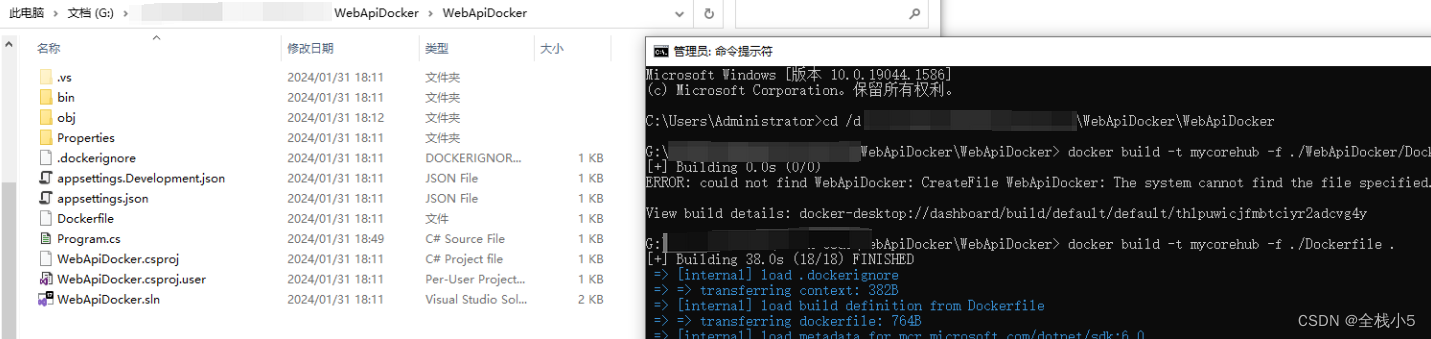
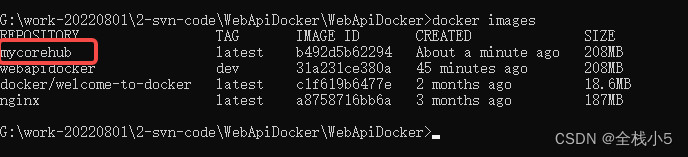
cmd查看容器镜像：docker images
如果能够查看到自己容器镜像名称，那么说明打包成功，并且在Docker Desktop镜像列表也会有一条记录

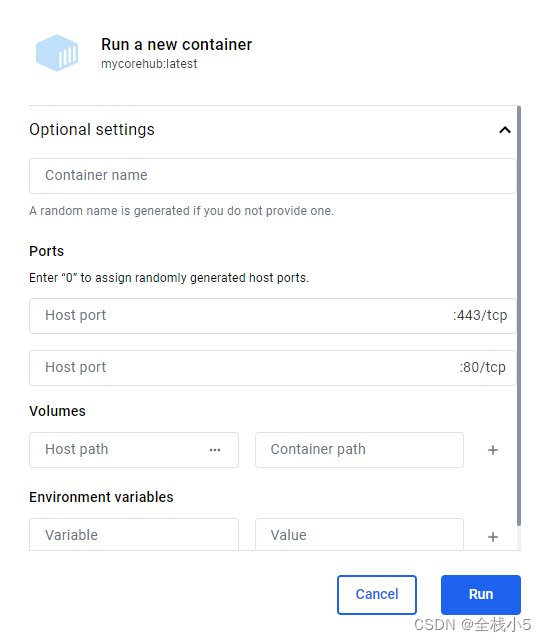
部署启动

打包生成好容器镜像后，点击Actions按钮会弹出下面窗口，填写好信息后会生成容器，特别是填写端口号

访问接口

可以看到有乱码，这里留个疑问，小伙伴们可以想下如何解决！

相关文章

【Docker】linux、nginx、容器镜像三者基本概念
【Docker】在Windows下使用Docker Desktop创建nginx容器并访问默认网站
【Docker】在Windows操作系统上安装Docker
【Docker】了解Docker Desktop桌面应用程序，TA是如何管理和运行Docker容器（1）

总结：温故而知新，不同阶段重温知识点，会有不一样的认识和理解，博主将巩固一遍知识点，并以实践方式和大家分享，若能有所帮助和收获，这将是博主最大的创作动力和荣幸。也期待认识更多优秀新老博主。