目录
1翻转二叉树
2对称二叉树
3二叉树的深度
最大深度
最小深度
4二叉树的结点数量
完全二叉树的结点数量
5平衡二叉树
6 中序 后序求前序
二叉树结构体如下:
struct freenode {int data;struct freenode *lchild, *rchild;//左孩子 右孩子
}T;1翻转二叉树
给你一个二叉树,让你向如图这样进行翻转

思路
给一个二叉树进行翻转,实际就是交换每个结点的左右孩子指针,遍历使用前序,后序;中序比较麻烦
伪代码如下:
先序遍历
void nb(struct freenode *T)//传入根结点
{if (T == NULL)//如果结点指针为空直接结束return;struct freenode *t;t = T->lchild; T->lchild = T->rchild; T->rchild = t;nb(T->lchild);//左孩子nb(T->rchild);//右孩子return;
}
后序遍历
void nb(struct freenode *T)//传入根结点
{if (T == NULL)//如果结点指针为空直接结束return;nb(T->lchild);//左孩子nb(T->rchild);//右孩子struct freenode *t;//定义t用于交换t = T->lchild; T->lchild = T->rchild; T->rchild = t;return;
}
2对称二叉树
给你一个二叉树,判断二叉树是否对称

思路
判断二叉树是否对称,根据图片可以看出,只需判断根结点的左右子树是否互为翻转,注意只能使用后序遍历,因为只有左右子树结点全部比较完才能确定是否为对称二叉树。
伪代码如下
//1为对称,0为不对称
int nb(struct freenode *p, struct freenode* q)//传入根结点的左右孩子
{if (p == NULL && q != NULL || p != NULL && q == NULL)//一边为空一边不为空return 0;else if (p == NULL && q == NULL)//两边同时为空return 1;else if (p->data != q->data)//两边都不为空且两边值不相等return 0;//剩下的两边都不为空且值相等还要继续判断int x, y;x = nb(p->lchild, q->rchild);//左结点的左孩子和右结点的右孩子比较y = nb(p->rchild, q->lchild);//左结点的右孩子和右结点的左孩子比较if (x == 1 && y == 1)return 1;elsereturn 0;
}
3二叉树的深度
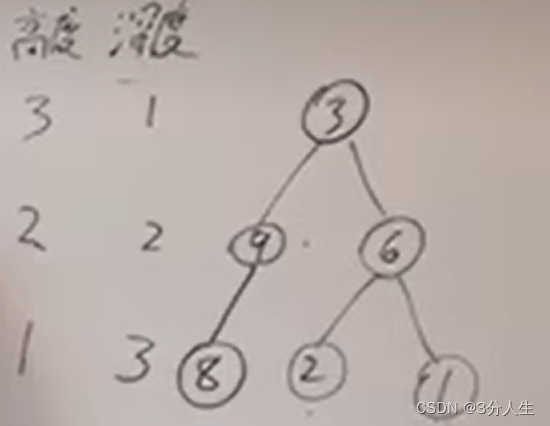
最大深度
思路
采用后序遍历,递归调用并返回每次最大深度
伪代码如下
int nb(struct freenode* T)//传入根结点
{if (T == NULL)//为空返回0return 0;return max(nb(T->lchild), nb(T->rchild)) + 1;//max返回两者较大值
}
最小深度
思路
求最小深度并不是将求最大深度的max改成min就行了,首先最小深度是指从根结点到叶子结点的最小值,如果只把求最大值的max改成min按照下面这个图得到的结果为1,而实际结果应该为3,我们知道叶子结点是没有左孩子和右孩子的,求最小深度问题就等价与求叶子结点,所以说在递归返回时如果没有左右孩子就返回零,如果只有其中一个孩子就返回那个孩子的值,如果有两个孩子就返回较小的那个,具体操作看代码
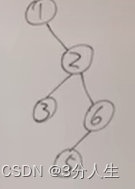
int nb(struct freenode* T)//传入根结点
{if (T->lchild == NULL && T->rchild == NULL)//没有左右孩子返回0return 0;else if (T->lchild != NULL && T->rchild == NULL)//没有右孩子,返回左孩子return nb(T->lchild);else if (T->lchild == NULL && T->rchild != NULL)//没有左孩子,返回右孩子return nb(T->rchild);return min(nb(T->lchild), nb(T->rchild)) + 1;//两个孩子都有,返回较小者
}4二叉树的结点数量
给你一个二叉树,让你求二叉树的结点数量
思路
前序,中序,后序遍历都可以,后序遍历代码相对简洁一点,从根结点传入,按照递归三部曲
1,确定函数参数和返回类型:参数显然就是从根结点传入,我们要去求结点数量,返回的值肯定就是结点数,为int型
2,递归结束的条件:显然就是结点为空时返回0
3,单层递归逻辑:我们要去求结点数量,而每一层递归求得就是左子树结点的数量+右子树结点的数量+这个结点本身
代码如下(后序)
int nb(struct freenode* T)//传入根结点
{if (T == NULL)//为空返回0return 0;//返回左子树结点的数量和右子树结点的数量加上结点本身return nb(T->lchild) + nb(T->rchild) + 1;
}
完全二叉树的结点数量
对于求完全二叉树的结点数量,可以像上面那样用求二叉树结点数量的方法,不过还可以换种方法让代码运行的更快,我们知道一个满二叉树的结点数量为2^n-1(n为二叉树深度),一个完全二叉树按照左右子树递归拆分,肯定会有满二叉树,所以说在递归过程中遇到满二叉树直接返回2^n-1这样就可以节约时间,问题也就转换成如何判断子树为满二叉树了,完全二叉树的子树肯定也是完全二叉树,而判断一个完全二叉树是否为满二叉树,只需要判断二叉树最左下角的那个结点和最右下角的那个结点的深度是否一样。思路讲完上代码
int nb(struct freenode* T)//传入根结点
{if (T == NULL)//为空返回0return 0;struct freenode* left, * right;int sum1 = 1, sum2 = 1;left = T->lchild; right = T->rchild;while (left) //记录最左下角结点的深度{sum1++;left = left->lchild;}while (right)//记录最右下角结点的深度{sum2++;right = right->rchild;}if (sum1 == sum2)return pow(2, sum1) - 1;return nb(T->lchild) + nb(T->rchild) + 1;//返回左子树结点的数量和右子树结点的数量加上结点本身
}
5平衡二叉树
给你一个二叉树,判断二叉树是否为平衡二叉树
思路
平衡二叉树是指二叉树任何结点的左右子树高度差不超过1
判断一个二叉树是否为平衡二叉树也是根据定义来判断的,一个结点的高度是指到叶子结点的距离,求高度采用后序遍历。
代码如下
//-1代表不是平衡二叉树
int nb(struct freenode* T)//传入根结点
{if (T == NULL)//为空返回高度为0return 0;int left = nb(T->lchild);if (left == -1)//只要左子树的子树不为平衡树,那么这个树一定不为平衡树return -1;int right = nb(T->rchild);if (right == -1)//只要右子树的子树不为平衡树,那么这个树一定不为平衡树return -1;if (abs(left - right) > 1)//高度差大于1,不为平衡树返回-1return -1;return max(nb(T->lchild), nb(T->rchild)) + 1;//取左子树和右子树高度的较大值+1为本结点的高度
}
6 中序 后序求前序
已知二叉树的中序和后序遍历结果,求前序遍历

我们知道已知中序,后序可以确定唯一前序遍历结果,中前,中层也可以,前后不能确定唯一的中序
思路
后序遍历中的最后一个数一定是根结点,而在中序遍历中知道根结点是哪一个,又可以大致拆成左右两部分,根据中序拆成两部分又可以把后序拆成两部分,如此反复正是一个递归的过程,
模板题 洛谷P1030 求先序排列
题目描述
给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,且二叉树的节点个数 ≤8)。
输入格式
共两行,均为大写字母组成的字符串,表示一棵二叉树的中序与后序排列。
输出格式
共一行一个字符串,表示一棵二叉树的先序。
输入输出样例
输入 #1
BADC BDCA
输出 #1
ABCD
说明/提示
【题目来源】
NOIP 2001 普及组第三题
#include<stdio.h>
#include<string.h>
char a[35], b[35];
void nb(int s1, int r1, int s2, int r2)//分别为中序后序的区间,左闭右开
{if (s1 >= r1)//为空时结束return;int i, j;for (i = s1; i < r1; i++){if (a[i] == b[r2 - 1])//找到根结点,中序遍历拆成两部分{printf("%c", a[i]);break;}}for (j = s2; j < r2; j++){if (r2 - j == r1 - i)//根据中序遍历拆分后序遍历break;}nb(s1, i, s2, j);//递归调用,左半部分nb(i + 1, r1, j, r2-1);递归调用,右半部分return;
}
int main()
{scanf("%s %s", a, b);int k, h;k = strlen(a);h = strlen(b);nb(0, k, 0, h);return 0;
}已知中序,前序求后序,思路大概也是如此,只是根结点为先序的第一个值






窗)
)
错误【已解决】)









坐216路公交车去买3.5元一斤的西红柿——C++中如何表达各种数值数据 3.3 数值数据类型)
