目录
二维前缀和原理
②牛客DP35 【模板】二维前缀和
解析代码
二维前缀和原理
在一维数组前缀和算法的基础上，想到：计算二维数组前缀和，不就和计算一维数组前缀和一样，即计算每一个位置的前缀和就相当于：
此位置的前缀和 = 这个位置的值 + 此位置前的前缀和
Eg：s[3][1] = a[0][0] + a[0][1] + a[0][2] + a[0][3] +a[1][1] + a[1][2] + …… + a[3][1]
但事实真的是这样吗？其实不是的，如果按照上述的方式去计算二维数组前缀和的话，本质其实就相当于遍历了一次二维数组，其时间复杂度就为O(N*M)了，其实已经偏离了前缀和的本心了
所以，在这里我们计算前缀和采取了另外一种计算策略：拼接
简单来说，就是遵循：计算哪个点的前缀和，就以这个点的横纵左边为边界，计算此点与起点（[1，1]）之间所形成的矩阵内所有元素的和 的原则。
简单图解：这里把矩阵的最上面和最左边添加上一行和一列 0，这样可以省去很多的边界处理。
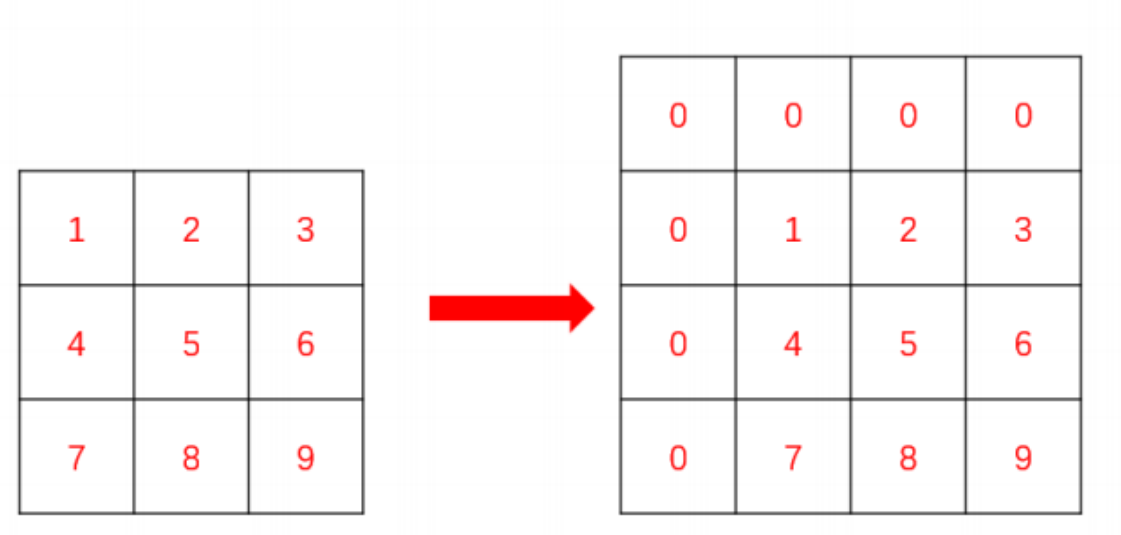
预处理出二维前缀和数组：
使用二维前缀和数组：
综上，便可以得出两条递推公式
计算某一个位置的前缀和：
dp[i, j] = 第i行j列格子与起点（[1,1]）所围成的矩阵中所有元素的和
dp[ i ][ j ] = dp[ i - 1 ] [ j ] + dp[ i ] [ j - 1] + arr[ i ] [ j ] - dp [ i - 1] [ j - 1];
计算某一区间的前缀和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
dp[ x2 ] [ y2 ] - dp[ x1 - 1 ] [ y2 ] - dp[ x2 ] [ y1 - 1] + dp[ x1 - 1] [ y1 - 1]
②牛客DP35 【模板】二维前缀和
【模板】二维前缀和_牛客题霸_牛客网
#include <iostream>
using namespace std;int main() {int a, b;while (cin >> a >> b) { // 注意 while 处理多个 casecout << a + b << endl;}
}
// 64 位输出请用 printf("%lld")解析代码
想到高中数学的一句话：手中无图，心中有图。想着图敲上面的公式就行了。
#include <iostream>
#include <vector>
using namespace std;int main()
{int n = 0, m = 0, q = 0;cin >> n >> m >> q;vector<vector<int>> arr(n + 1, vector<int>(m + 1, 0));for(int i = 1; i <= n; ++i) // 读数据{for(int j = 1; j <= m; ++j){cin >> arr[i][j]; }}vector<vector<long long>> dp(n + 1, vector<long long>(m + 1, 0));for(int i = 1; i <= n; ++i) // 构成前缀和数组{for(int j = 1; j <= m; ++j){dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];}}int x1 = 0, y1 = 0, x2 = 0, y2 = 0;while(q--) // 使用前缀和数组查询{cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] << endl;}return 0;
}
