前言

DevEco Studio版本：4.0.0.600

使用效果

如何使用

参考文档：OpenHarmony http数据请求

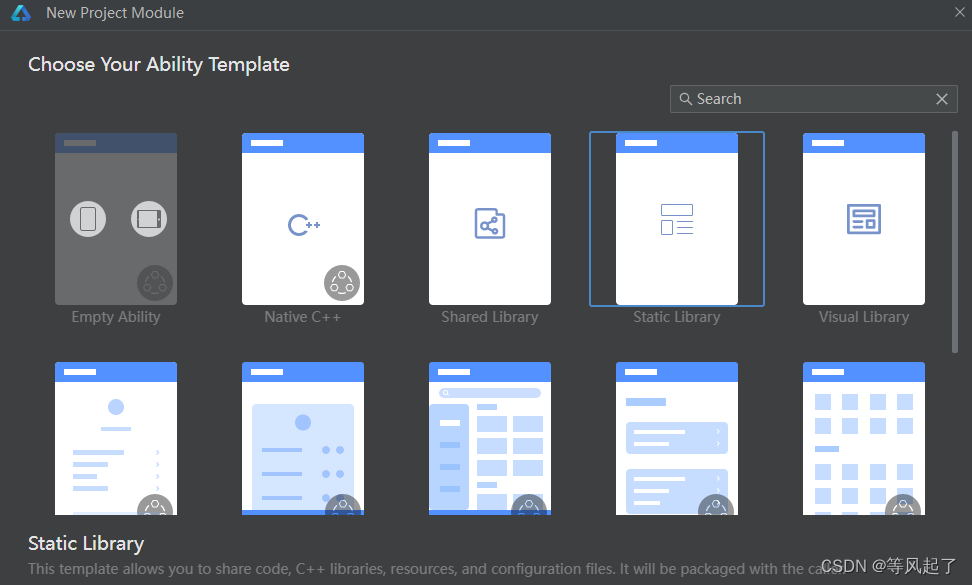
1、module创建

File-->New-->Module，选择Static Library

2、相关类创建

HttpCore：Http的核心类，用于http的请求

RequestMethod：http请求的类型，包含：GET、POST等

RequestOptions：http的请求配置，包含：请求的url、请求头等

HttpManager：Http请求的管理类

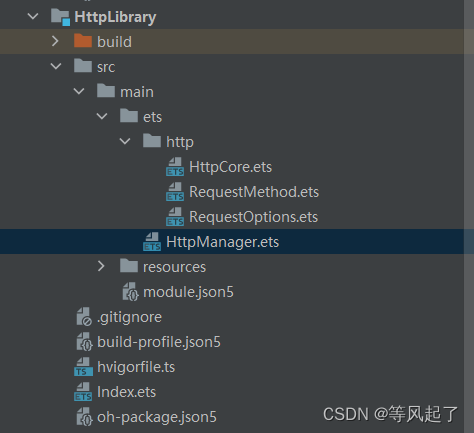
然后在HttpLibrary的Index.ets类中添加对外输出的引用

export { HttpManager } from './src/main/ets/HttpManager'export { RequestMethod } from './src/main/ets/http/RequestMethod'

HttpCore类：

import http from '@ohos.net.http';
import { RequestOptions } from './RequestOptions';/*** Http请求器*/
export class HttpCore {/*** 发送请求*/request<T>(requestOption: RequestOptions): Promise<T> {