辅助定理
增益=Gm*输出阻抗
输出短路求Gm
输入置0求输出阻抗
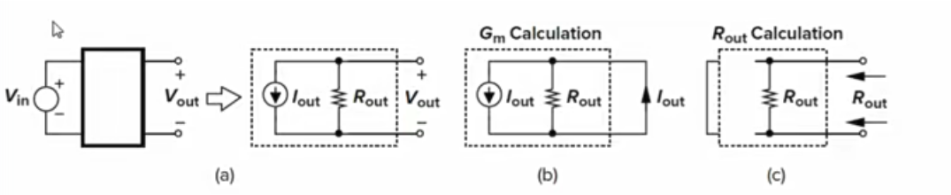
求源极负反馈的增益
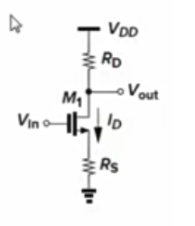
随着Vin的增加,Id也在增加,Rs上压降增加,所以,Vin的一部分电压体现在Rs上,而不是全部作为Vgs,因此导致Id变得平滑。
Rs足够大的时候,Gm=1/Rs,跨导Gm线性化,Gm的线性度是以牺牲增益为代价的。用增益换线性度。
源极负反馈的一个主要作用时增加共源极的输出阻抗,将Rs换成一个MOS管,就是我们常见的Cascode结构。总输出阻抗是上式并联RD。
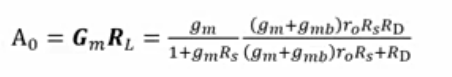
当RD远远小于Rout时,增益≈RD/RS。当RD远远大于Rout时,增益≈gmro,为MOS管本征增益。相当于源极负反馈对输出电阻的增强刚好抵消其对跨导的衰减。
Cascode OTA
DC分析
用辅助定理求增益。
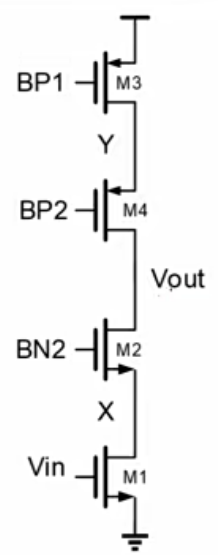
![]()
AC分析
考虑电容,主极点在输出极点。CL越大,主极点越低,因此GBW越小,稳定性越好。次级点在X点。
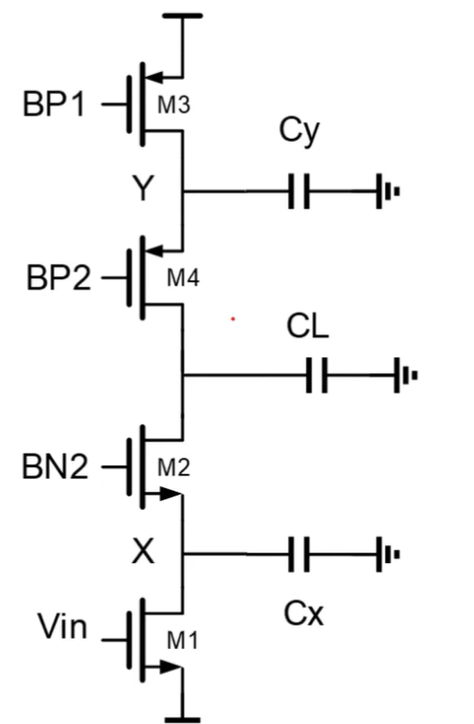

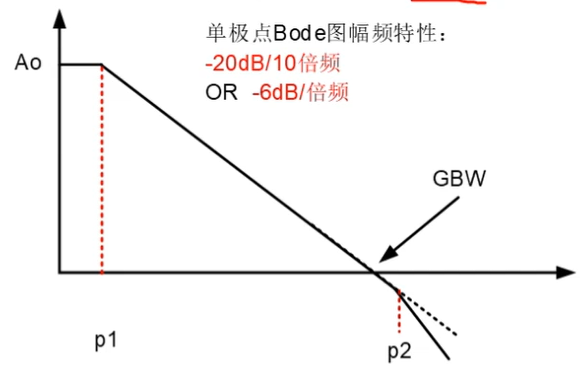
问题:为什么Y点没有引入次级点,M1和M2构成信号通路,M3恒润M4构成负载通路,负载通路的极点对频率特性无影响吗?Cy可以无穷大?
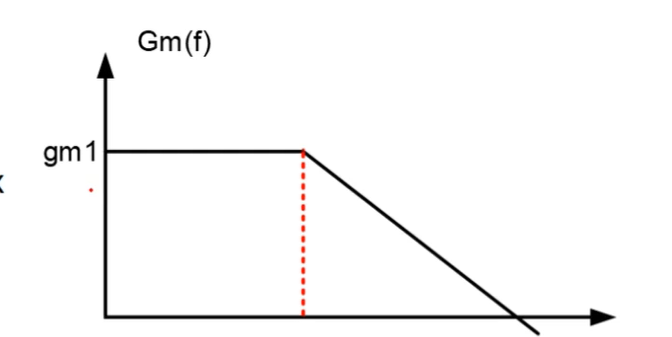
求Gm
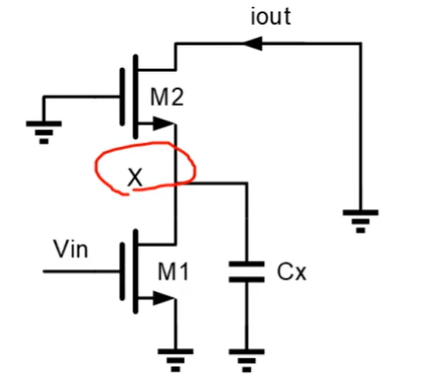
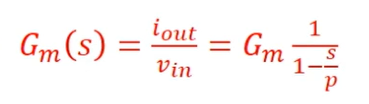
![]()
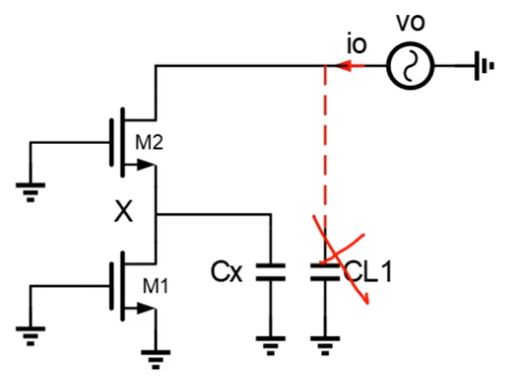
输出阻抗
考虑下半部分,首先忽略CL1,求出阻抗之后,再与CL1并联。
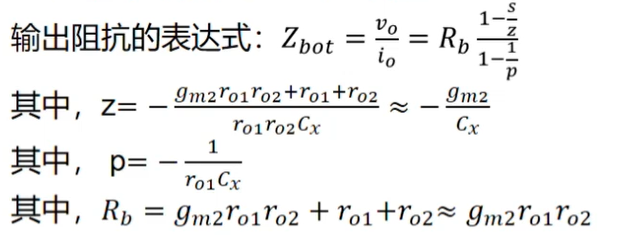
上述结果与CL1并联得到下图结果,p1b是主极点,p2b是次级点。
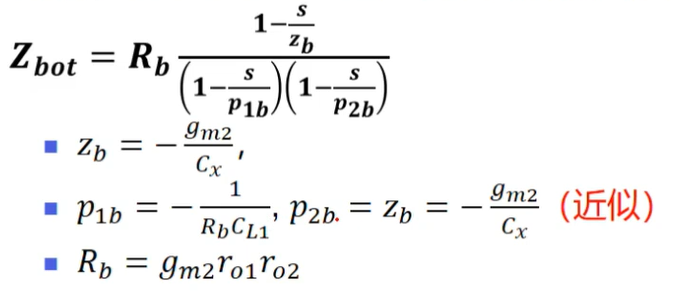
求OTA上半部分输出阻抗。
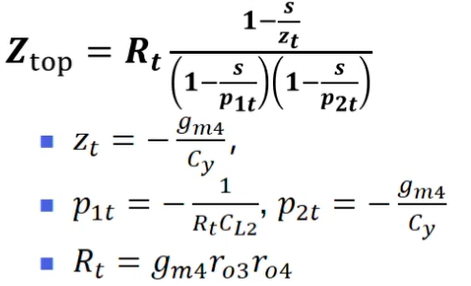
把上下两部分合并,阻抗合并后主极点也将合并,CL1和CL2合并。
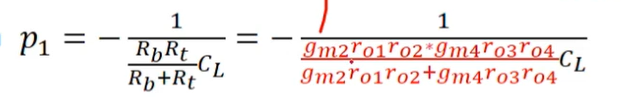
增益
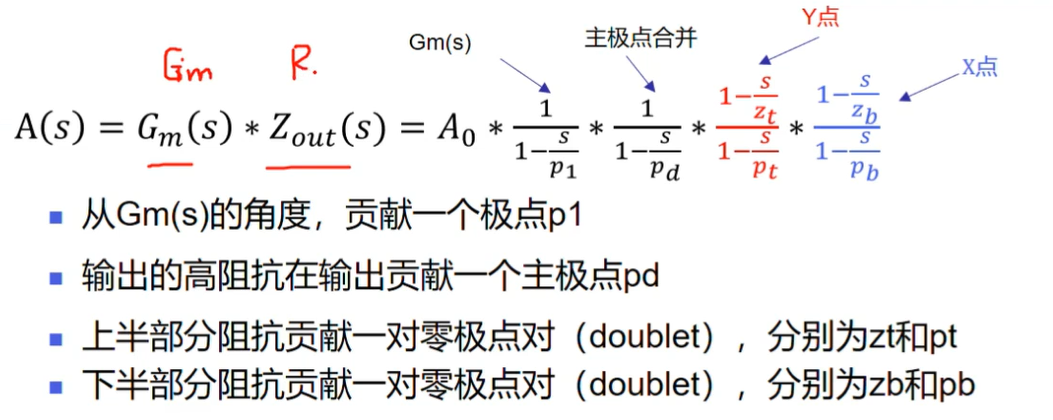
p1=zb,所以可以简化。Y点引入的零极点对近似相等,某种意义上可以抵消。

速度
饱和区,偏置电流一定的情况下,增益正比于WL,为了增大增益,需要增加MOS面积。
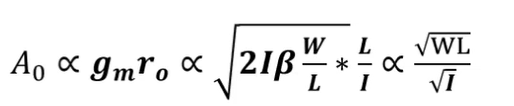
次级点表达式如下。
次级点p1越大,稳定性越好,为了增大次级点,所以需要减小M2的L。


噪声
M2不贡献噪声,所以只需要从增益和稳定性的角度去设计M2的尺寸。从噪声的角度考虑,R3的gm3要做小,gm1要做大。因为M3是负载管,M1是输入管。所以M3的宽长比要做小,M1的宽长比要做大。
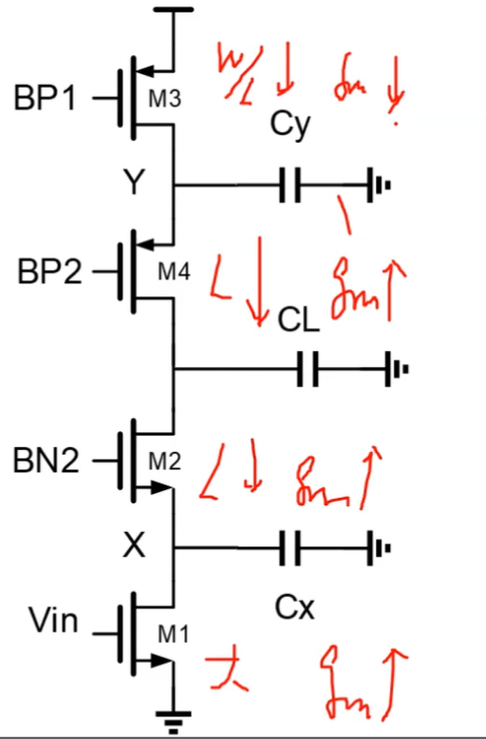
综上所示,M1宽长比要大,gm要大(增益、噪声);M2的L要小,gm要大(带宽稳定性、输出阻抗);M4同M2;M3的宽长比要小,gm要小(噪声)。
距离较近的零极点对
具体公式推导可参考:Kamath B, Meyer R G, Gray P R. Relationship between frequency response and settling time of operational amplifiers[J]. IEEE Journal of Solid-State Circuits, 1974, 9(6): 347-352.
频域特性
设置低频增益为1e3,主极点为1e3,零极点对在20e3左右、零点是20e3,极点是k*20e3。k的大小显示了零极点对的相对位置,查看k从0.8变化到1.2时的频率响应。
%%pole-zero doublet frequency responseclear;clc;
p1 = 1e3;
A0 = 1e3;
w_doublet = 20e3;
figure(1);
hold on;
for k = 0.8:0.1:1.2z2 = w_doublet;p2 = w_doublet*k;num = A0.*[1/z2,1];den = conv([1/p1,1],[1/p2,1]);tf_sys = tf(num , den);bode(tf_sys)
end
legend( 'k = 0.8',...'k = 0.9',...'k = 1 ',...'k = 1.1',...'k = 1.2')
%%
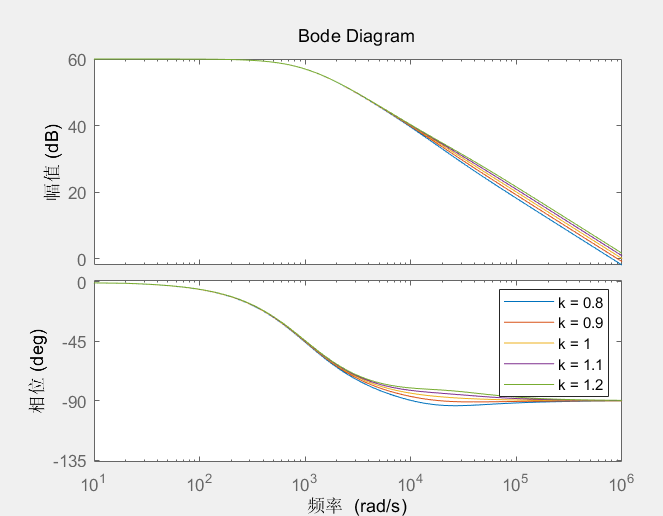
结论:零极点对,对频域特性响应有限
时域特性
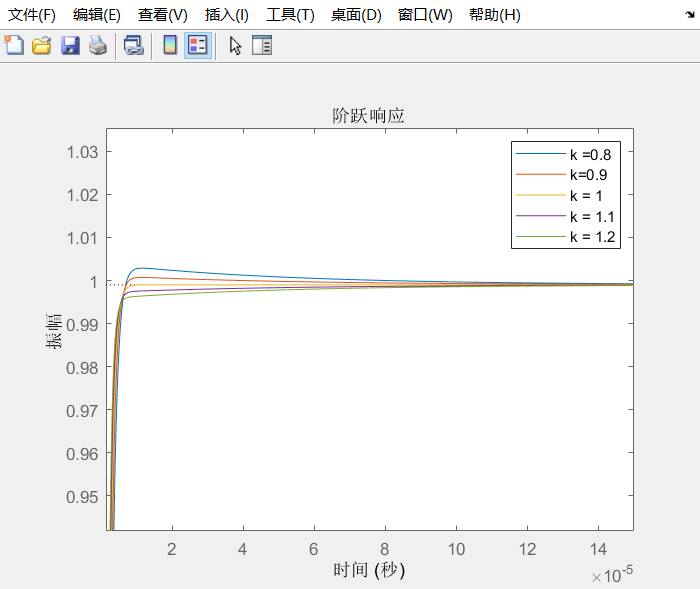
给阶跃信号,发现零极点对,对阶跃响应影响很大。这在采样电路设计中影响很大。
%%pole-zero doublet setting responseclear;clc;
p1=1e3;
A0 = 1e3;
w_doublet = 20e3;
k=1;
for k=0.8:0.1:1.2z2 = w_doublet;p2 = w_doublet*k ;num= A0.*[1/z2,1];den = conv([1/p1,1],[1/p2,1]);tf_sys = tf(num , den);tf_sys = tf_sys/(1+tf_sys)figure(1);hold on;t =0:1e-7:15e-5;step(tf_sys,t);
end
legend( 'k =0.8',...'k=0.9',...'k = 1',...'k = 1.1',...'k = 1.2')













 实战指南)
)




