今天在看一个比较常见的激活函数，叫作 sigmoid 激活函数，它的数学表达式为：

其中，x 为输入，画出图来看更直观一些。

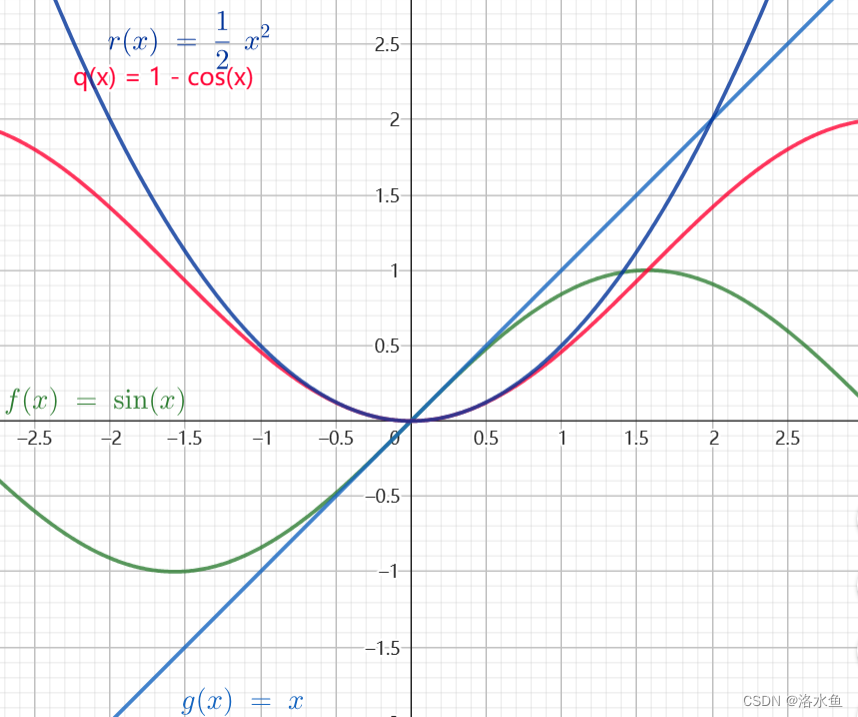
Sigmoid 函数的图像看起来像一个 S 形曲线，我们先分析一下这个函数的特点。

1. Sigmoid 函数的输出范围在 (0, 1) 之间，并且不等于0或1。

2. Sigmoid 很明显是一种非线性函数，因此也可以用来做激活。

3. Sigmoid 函数非常平滑，在整个实数范围内都是可导的。

从以上几个特点，可以看出 sigmoid 作为激活函数的一些优势。

1. Sigmoid 可用于二分类问题，因为它将输出映射到(0, 1)的概率范围，适用于模型输出表示概率的场景，如逻辑回归模型。

2. Sigmoid 在整个实数范围内都是可导的，这使得它可以与梯度下降等优化算法配合使用，便于模型参数的更新。

当