加法器的介绍与原理分析

什么是加法器？

加法器是一种数字电路，用于将两个二进制数相加并输出它们的和。

如何实现加法器

要讨论如何实现加法器就要先从只有一位的数字先进行考虑

一位二进制数相加

不考虑来自低位的进位——半加器

对于一位二进制数相加，由于是二进制有可能要进位也可能不需要进位，根据具体的情况如下图所示：

没有进位的话，把进位补上0：

转化为列表如下：

数字A	数字B	输出S	进位CO
1	0	1	0
0	1	1	0
0	0	0	0
1	1	0	1

对于一位数字的话我们使用A表示第一个数字，B表示第二个数字，S表示加和之后的当前位的和，CO表示向高位的进位，使用逻辑函数式那么
$$\begin{array}{rl}S& =A{B}^{\prime }+A^{\prime }B(异或操作)\\ CO& =AB(与操作)\end{array}$$
也就是说对于一位二进制数的加法，我们可以使用异或操作跟与操作求出加法结果。
逻辑电路如图所示：

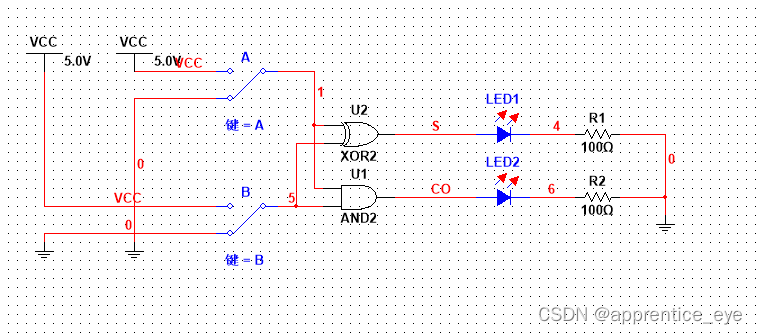
这样可以根据灯的亮灭判断到底输出了什么。
这样组成的期间就是半加器，但是半加器并没有考虑来自低位的进位，所以它的功能是不完善的。

考虑来自低位的进位——全加器

如果考虑到来自低位的进位那么输入就会有三个分别是数字A、数字B与进位CI。
相加的过程中我们可以看作先将数字A与数字B相加，相加得到的加和再与进位CI相加，即全加器由两个半加器组成。
真值表为：

数字A	数字B	进位CI	数字S	进位CO
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

根据真值表可以得到以下逻辑函数式
$$\begin{array}{rl}S& =A{B}^{\prime }C{I}^{\prime }+A^{\prime }BC{I}^{\prime }+A^{\prime }{B}^{\prime }CI+ABCI\\ CO& =ABC{I}^{\prime }+A^{\prime }BCI+A{B}^{\prime }CI+ABCI\end{array}$$
将逻辑表达式进行化简得到
$$\begin{array}{rl}S& =C{I}^{\prime }(A{B}^{\prime }+A^{\prime }B)+CI(A^{\prime }{B}^{\prime }+AB)\\ S& =C{I}^{\prime }(A{B}^{\prime }+A^{\prime }B)+CI(A{B}^{\prime }+A^{\prime }B{)}^{\prime }\\ S& =C{I}^{\prime }(A⨁B)+CI(A⨁B{)}^{\prime }\\ S& =CI⨁A⨁B\\ CO& =AB(C{I}^{\prime }+CI)+CI(A^{\prime }B+A{B}^{\prime })\\ CO& =AB+CI(A⨁B)\\ CO& =ABC{I}^{\prime }+A^{\prime }BCI+A{B}^{\prime }CI+ABCI\end{array}$$
最终我们得到的逻辑函数式为:
$$\begin{array}{rl}S& =CI⨁A⨁B\\ CO& =AB+CI(A⨁B)\end{array}$$
转化为电路图为：

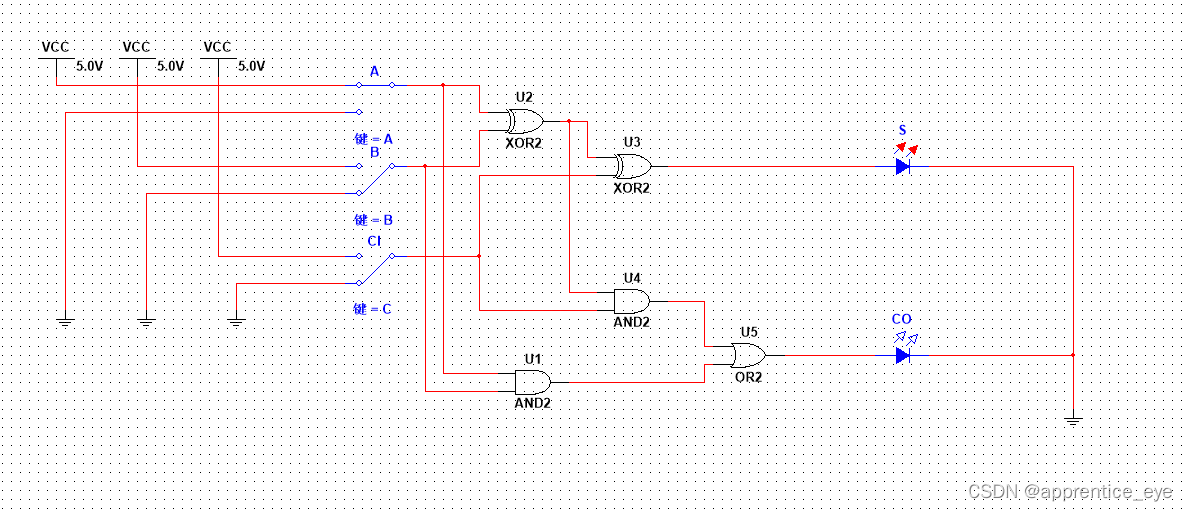
这样我们就得到了一个全加器。
有了半加器与全加器，就能着手实现二进制加法了。

四位二进制加法器

最低位相加是不需要考虑进位的，所以使用半加器就行，当然使用全加器也可以只不过进位CI要置零。
现在就着手实现四位二进制数加法器：
多位加法器的原理就是，有多个一位加法器组成，每个一位加法器负责多位中的一位的运算，运算的结果需要进位到下一位，然后下一位求出结果，很明显这是一种
电路图如下:

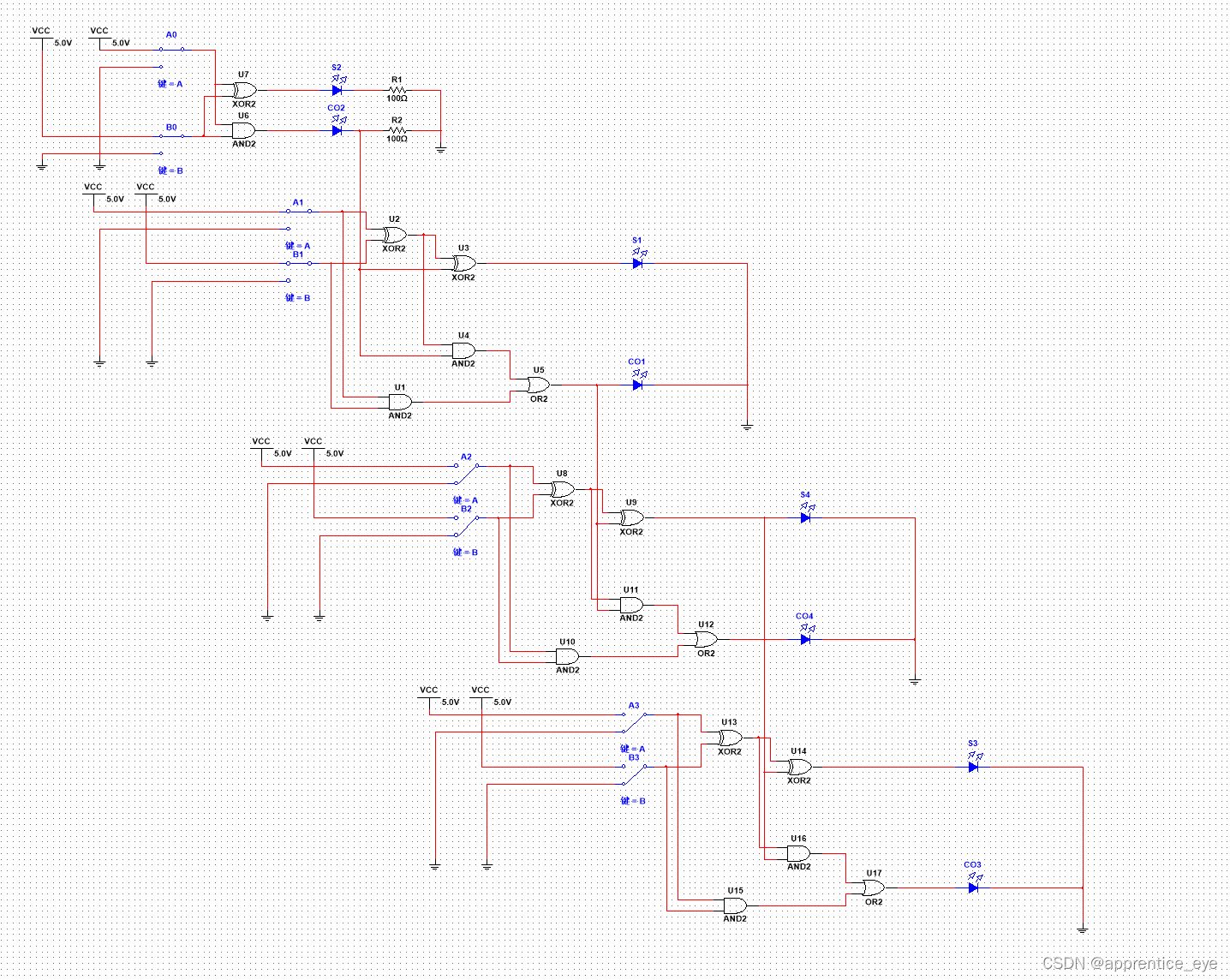
如图所示，但是此加法器是一种串联的结构，进行运算时高位需要等待低位求出运算结果才能得到高位的结果，也就是花费的时间比较多，有没有办法在进行低位运算的同时进行高位的运算。

超前进位四位加法器

如果我们不再使用先算低位进位，然后再算高位，而是直接根据低位数字直接算出应该到高位的进位，这样就能将串行结构改成并行结构，这样就能够大大减少运算所需的时间。

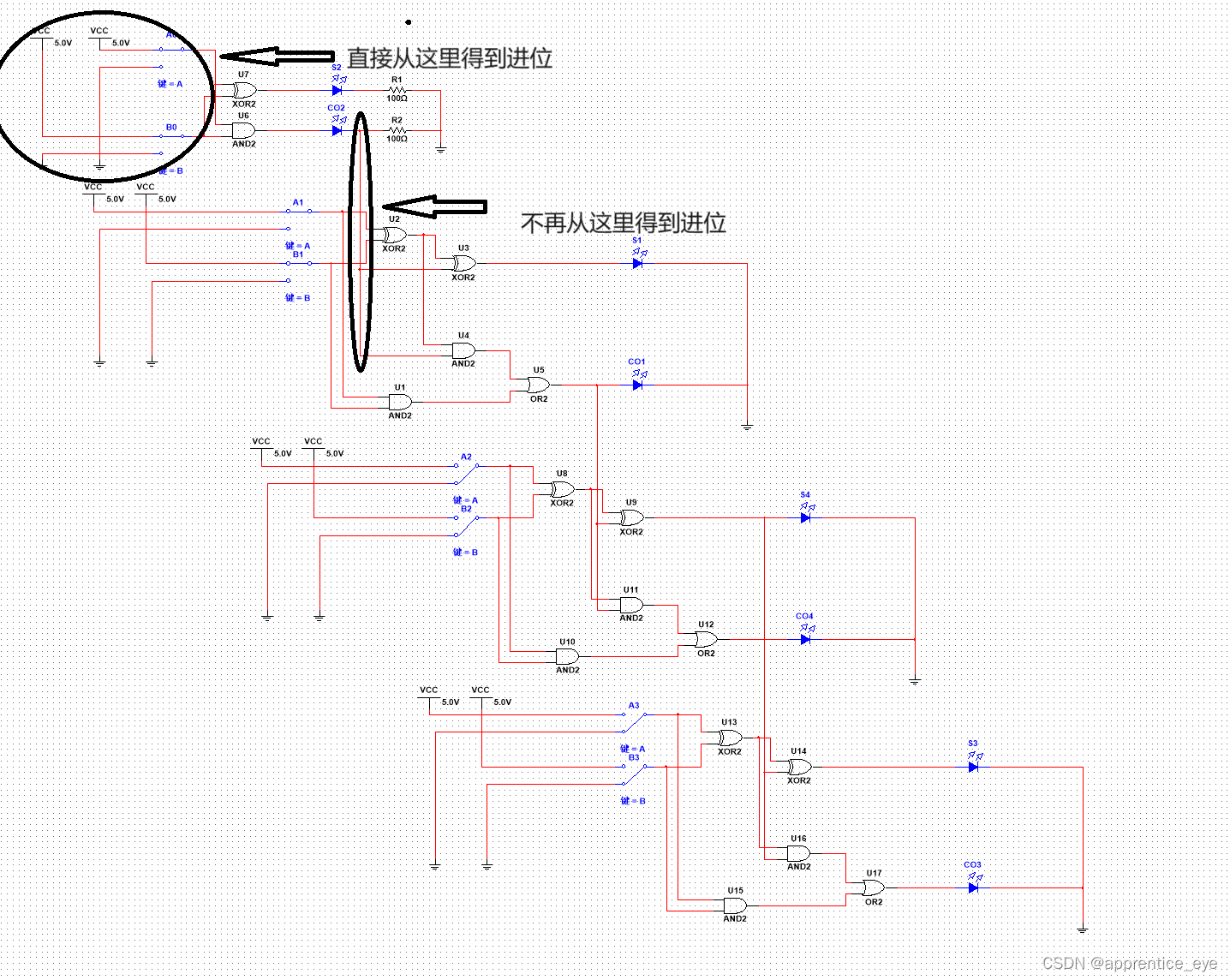
这样我们就能够将结构改成下面的样子：

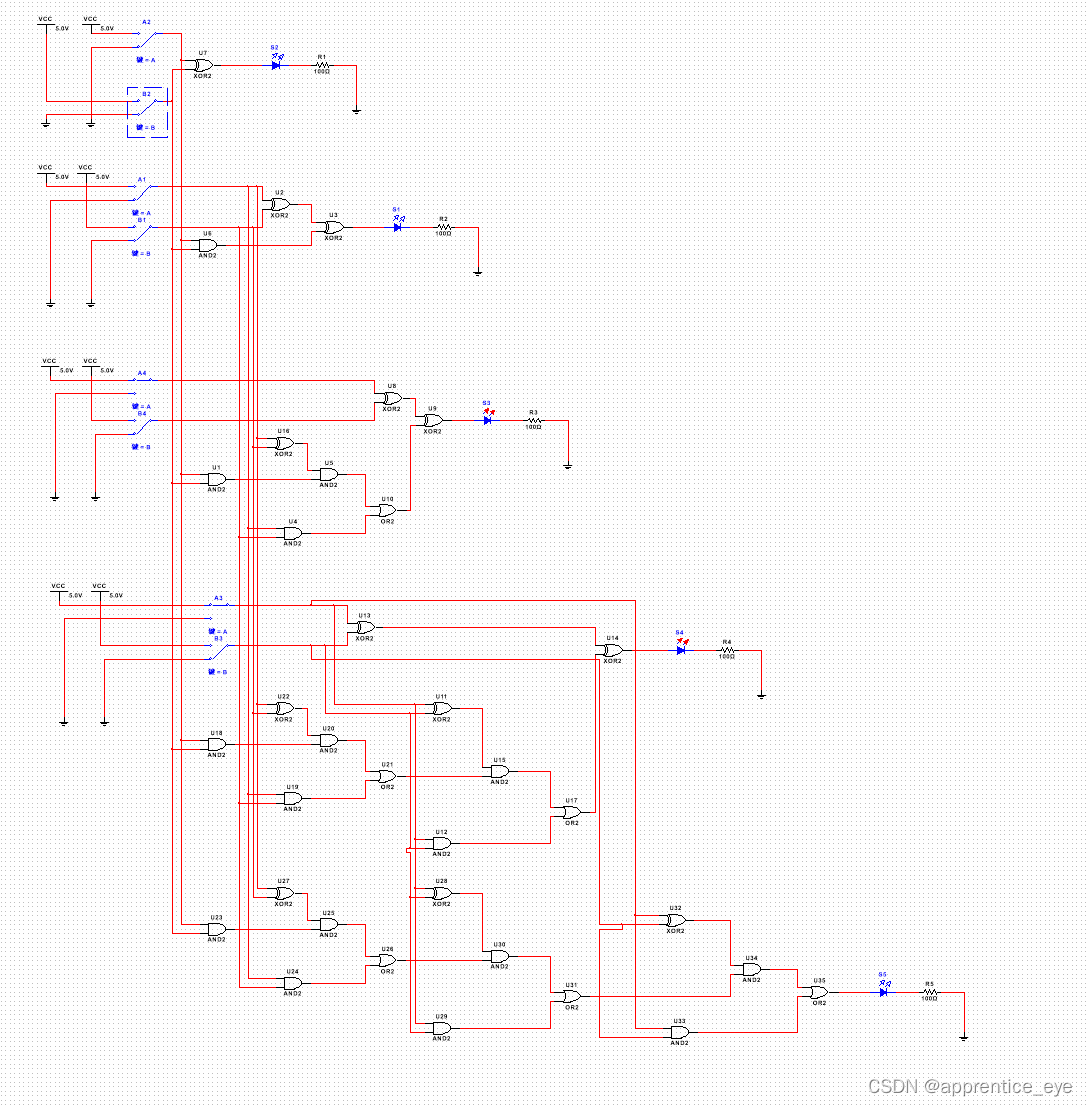
从图中我们可以看出是根据原始输入计算的进位，而不是一位一位进行计算的进位，这样每一位数字就可以同时计算，这样就可以在一个时钟周期内完成加法运算。
但是这一个明显优缺点，到后面计算进位的电路越来越复杂。
至此关于加法器的原理就讲完了。

注：如果电路图，或者逻辑函数式有写错的，请在评论区@我，我会尽快修改的。
multisim电路仿真图可以在我的GitHub的项目中下载：电路仿真图

如果有什么地方讲的不好或者讲错的地方欢迎大家指出来，如果我所讲的对你们有帮助不要忘了点赞、收藏、关注哦！
我是你们的好伙伴apprentice_eye
一个致力于让知识变的易懂的博主。