【详解】KMP算法——每步配图让你打穿KMP

介绍

什么是KMP算法：

KMP算法主要运用串的模式匹配中（简单来说就是在s串中找到一个与t串相等的子串，称为模式匹配）例如s为abcdef，t为bcd，那么就是在s中找到bcd，并返回其在s中的首下标，该算法和BF算法相比有比较大的改进，主要是消除了主串指针的回溯，从而使算法的效率有了某种程度的提高。（了解这些就够了，其他都是废话）

有些读者可能不了解什么使BF算法，下面我简单讲解一下（了解的读者可跳过）

BF算法

可以看到BF算法其实就是类似遍历（一定可行，但是时间复杂度是O（m*n）m为s的字符个数，n为t的字符个数）效率太低了，KMP算法就是对它的改进

思维图如下：

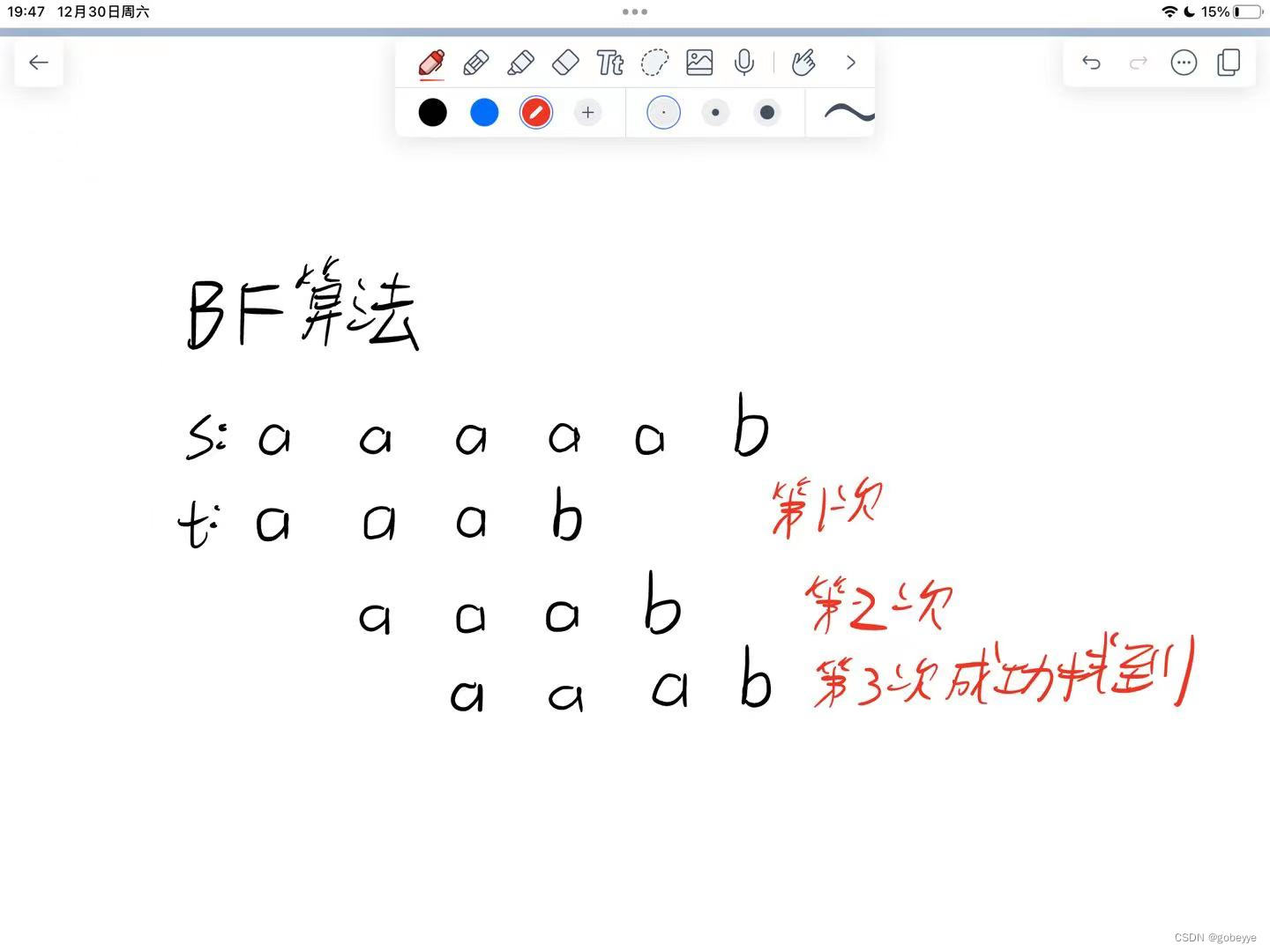
代码如下（解释都在代码里了）

#define  _CRT_SECURE_NO_WARNINGS 1
//BF算法
#include <stdio.h>
#include <string.h>
typedef struct
{char data[1000];int length;
}SqString;
int index(SqString s, SqString t)
{int i = 0, j = 0;while (i < s.length && j < t.length){if (s.data[i] == t.data[j])  	//继续匹配下一个字符{i++;				//主串和子串依次匹配下一个字符j++;}else          			//主串、子串指针回溯重新开始下一次匹配{i = i - j + 1;			//主串从下一个位置开始匹配j = 0; 				//子串从头开始匹配}}if (j >= t.length)return(i - t.length);  		//返回匹配的第一个字符的下标elsereturn(-1);        		//模式匹配不成功
}
int main()
{SqString s, t;strcpy(s.data, "ababcabcacbab");strcpy(t.data, "abcac");s.length = 13;t.length = 5;printf("位置:%d\n", index(s, t));return 1;
}

接着就是我们的重头戏KMP算法，了解了BF算法，我们发现每次比较完，若不匹配，指向s的指针要进行回溯，那有没有办法让指向s的指针不回溯，一直向前这样是不是效率就会高很多。

KMP算法

分为两步

第一步：求next数组（是关于t串的数组）

我先给出代码（如果理解这个代码直接看第二步）

一开始看不懂很正常（因为非常抽象，花掉一个早上理解这个代码都算正常的）

求解next数组代码如下（别小看这个和递归一样小小代码，大大能量）

void GetNext(SqString t, int next[])
{int j, k;j = 0, k = -1;next[0] = -1;while (j < t.length - 1){if (k == -1 || t.data[j] == t.data[k]){k++; j++;next[j] = k;}else k = next[k];}
}

为什么要求next数组呢，这是因为KMP算法比较过程其实是让t串进行移动（理解这个非常重要），next数组存储当前可以移动多少个字符。

概念：对于t[j]的每个字符存在一个整数k，使得模式串t中开头的k个字符（t[0]，t[1]，...，t[k-1]）依次与t[j]的前面k个字符（t[j-k]，t[j-k+1]....t[j-1]，这里t[j-k]最多从t[1]开始）。如果这样的k有多个取最大的一个，模式串t中每个位置j的字符都有这种信息，采用next[j]数组表示,及next[j] = MAX(k).

概念如上，不理解很正常下面我会用图画来帮助大家理解（包括我从不懂到理解的一些经验）

首先总体next我先给出下面会逐一分析

总体next（不懂没关系看下面的）

规定next[0]为-1，这是规定不必深究，B前面只有A，故next[1]为0

找k的规则，大一点的看的比较清楚，我就先讲为什么下标7的B下面的k为什么为3，找的时候一个必须从0开始，另一个的结尾必须是下标7的前一个，7下标对应的k是反应前6个，不包括本身。

其中特别注意（从0开始的哪个不能超过j，从j前面为结尾的不能往前到0），这其实就是前后缀的概念（防止太乱我给了两张图片）

第一步：

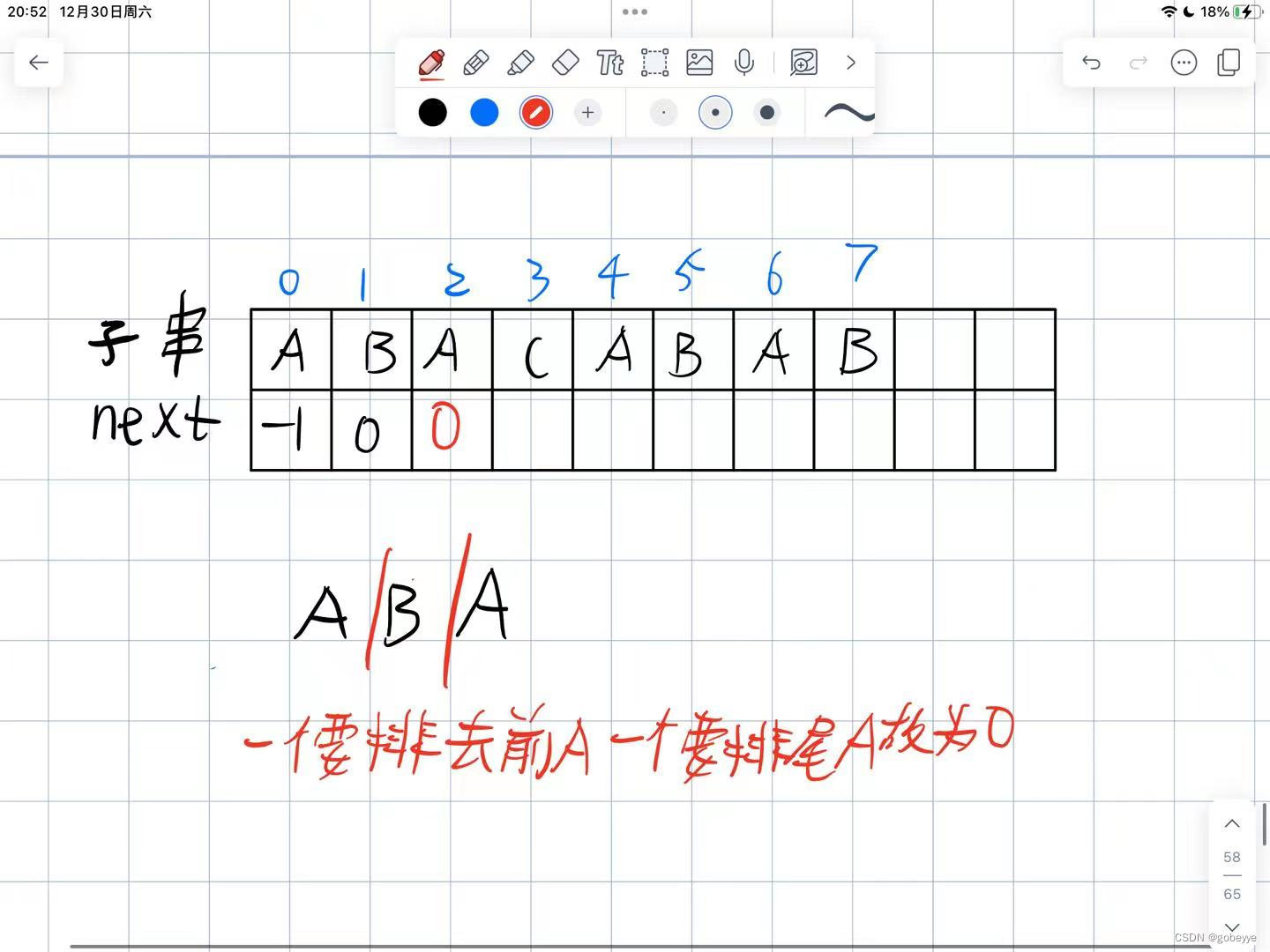
next【0】规定为-1，next【1】前面只有A显然为0自己本身不算相等，next【2】要记得我上面讲的前后缀

第二步：

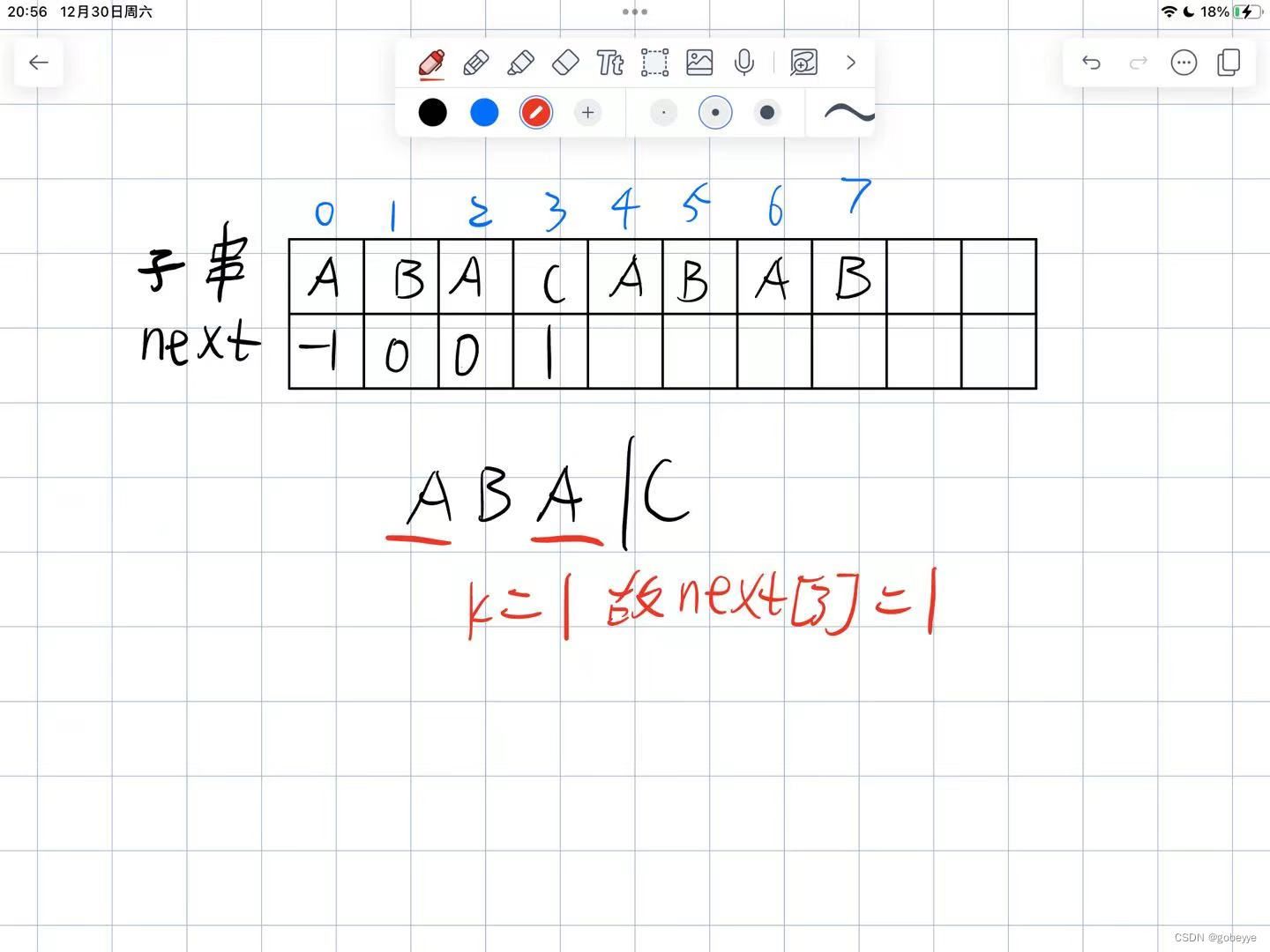
后面类似，就麻烦读者自行完成。

将上面的图解归纳起来就得到了一个求解next数组的公式

下面那个代码再理解理解（上是手算，下面是代码实现要理解一下，特别注意k每次最多增加1，k=next【k】是k回退，因为不相等，读者可以自己画图帮助理解一下）

void GetNext(SqString t, int next[])
{int j, k;j = 0, k = -1;next[0] = -1;while (j < t.length - 1){if (k == -1 || t.data[j] == t.data[k]){k++; j++;next[j] = k;}else k = next[k];}
}

接着就是

第二步KMP算法的模式匹配过程

一样我先给代码

int KMPIndex(SqString s, SqString t)
{int i = 0, j = 0;int next[20];GetNext(t, next);while (i < s.length && j < t.length){if (j == -1 || s.data[i] == t.data[j]){j++; i++;}else j = next[j];}if (j >= t.length) return (i-t.length);else return -1;
}

有了next数组的帮助，我们就可以知道当模式串t与s串不同时，t串要向右移动多少个字符

整个过程图解如下：

相信细心的同学发现KMP算法其实是移动t串，s串是一直向前的。

总代码如下

c语言

#define  _CRT_SECURE_NO_WARNINGS 1
//串的模式匹配
//kmp求解
#include <stdio.h>
#include <string.h>
typedef struct
{char data[1000];int length;
}SqString;
void GetNext(SqString t, int next[])
{int j, k;j = 0, k = -1;next[0] = -1;while (j < t.length - 1){if (k == -1 || t.data[j] == t.data[k]){k++; j++;next[j] = k;}else k = next[k];}
}
int KMPIndex(SqString s, SqString t)
{int i = 0, j = 0;int next[20];GetNext(t, next);while (i < s.length && j < t.length){if (j == -1 || s.data[i] == t.data[j]){j++; i++;}else j = next[j];}if (j >= t.length) return (i - t.length);else return -1;
}
int main()
{SqString s1, s2;strcpy(s1.data, "abcdefg");strcpy(s2.data, "de");s1.length = 7;s2.length = 2;int t = KMPIndex(s1, s2);printf("%d", t);return 0;
}

c++版的如下

//KMP算法
#include "sqstring.cpp"
void GetNext(SqString t,int next[])		//由模式串t求出next值
{int j,k;j=0;k=-1;next[0]=-1;while (j<t.length-1) {	if (k==-1 || t.data[j]==t.data[k]) 	//k为-1或比较的字符相等时{printf("(1)j=%d,k=%d,两个指向字符相同",j,k);printf(",执行j++,k++ -> ");j++;k++;next[j]=k;printf("(1) j=%d,k=%d,next[%d]=%d\n",j,k,j,k);}else{printf("(2)j=%d,k=next[%d]=",j,k);k=next[k];printf("%d\n",k);}}
}
int KMPIndex(SqString s,SqString t)  //KMP算法
{int next[MaxSize],i=0,j=0;GetNext(t,next);while (i<s.length && j<t.length) {if (j==-1 || s.data[i]==t.data[j]) {i++;j++;  			//i,j各增1}else j=next[j]; 		//i不变,j后退}if (j>=t.length)return(i-t.length);  	//返回匹配模式串的首字符下标else  return(-1);        		//返回不匹配标志
}
/*
int main()
{SqString s,t;StrAssign(s,"ababcabcacbab");StrAssign(t,"abcac");printf("s:");DispStr(s);printf("t:");DispStr(t);printf("位置:%d\n",KMPIndex(s,t));return 1;
}
*/int main()
{SqString s,t;StrAssign(t,"aaba");//StrAssign(t,"aaaac");printf("t:");DispStr(t);int next[100];GetNext(t,next);return 1;
}