一、LSH 介绍

    LSH(Locality sensitive hashing)是局部敏感性hashing，它与传统的hash是不同的。传统hash的目的是希望得到O（1）的查找性能，将原始数据映射到相应的桶内。
    LSH的基本思想是将空间中原始数据相邻的2个数据点通过映射或者投影变换后，这两个数据点在新的空间中的相邻概率很大，不相邻的点映射到同一个桶的概率小。我们可以看到将一个在超大集合内查找相邻元素的问题转化为了在一个很小的集合内查找相邻元素的问题，显然计算量下降了很多。下面借用一幅图来表示：

LSH满足如下条件：
$if\quad d(x,y) \le d_1, then \quad P(h(x)=h(y))\ge P_1$
$if \quad d(x,y) \ge d_2, then\quad P(h(x)=h(y))\le P_2$
•其中d(x,y)表示x和y之间的距离，d1 < d2，h(x)和h(y)分别表示对x和y进行hash变换。
•满足以上两个条件的hash functions称为(d1,d2,p1,p2)-sensitive。而通过一个或多个(d1,d2,p1,p2)-sensitive的hash function对原始数据集合进行hashing生成一个或多个hash table的过程称为Locality-sensitive Hashing.

二、Simhash 算法

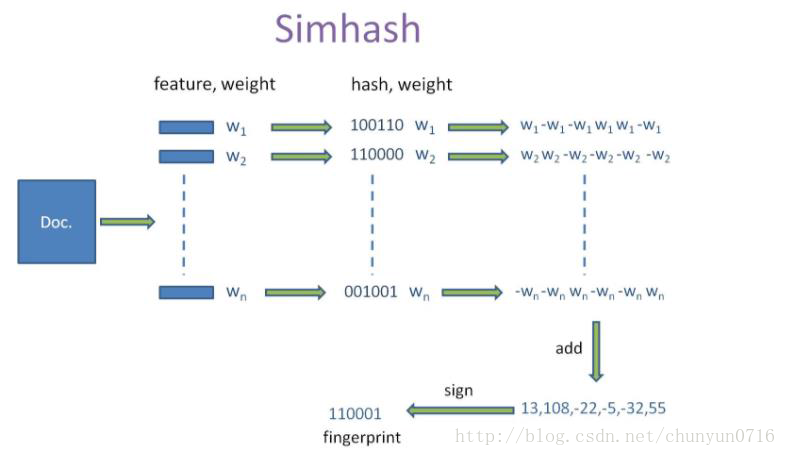
    SimHash 算法的输入是一个向量，输出是一个$f$位的签名值。设输入的是一个文档的特征集合，每个特征有一定的权重。
Simhash 算法如下：

1. 将一个$f$维向量$\vec v$初始化为$\vec0$, $f$位的二进制数$S$初始化为0
   • 对每一个特征:
     用传统的hash算法对该特征产生一个$f$位的签名$b$.
     对于$i=1 \quad to \quad f:$
     $\quad$如果$b$的第$i$位为1，则 $\vec v$$S$加上该特征的权重
     $\quad$否则，$\vec v$的第$i$个元素减去该特征的权重
   • 如果$\vec v$的第$i$个元素大于0， $S$ 的第$i$位为1，否则为0
   • 输出$S$作为签名

   • 如下图所示：
     

     SimHash是由随机超平面hash算法演变而来的，对于一个$n$维向量$\vec v$, 要得到一个f位的签名（$f <<n$）,算法如下：

     1.随机产生$f$个$n$维的向量$\vec r_1,\vec r_2,…,\vec r_f$
     2.对每一个向量$\vec r_i$，如果$\vec v$与$\vec r_i$的点积大于$0$，则最终签名的第$i$位为$1$，否则为$0$

         上述算法相当于随机产生了f个n维超平面，每个超平面将v所在的空间一分为二。v在这个超平面上方则得到一个1，否则得到一个0，然后将得到的f个0或1组合起来成为一个f维的签名。

         如果两个向量$\vec u, \vec v$的夹角为$\theta$，则一个随机超平面将它们分开的概率为$\frac{\theta}{\pi}$，因此$\vec u, \vec v$的签名的对应位不同的概率等于$\frac{\theta}{\pi}$，所以，我们可以用两个向量的签名的不同的对应位的数量，即汉明距离，来衡量这两个向量的差异程度。

         在simhash中并没有直接产生用于分割空间的随机向量，而是间接产生的：第k个特征的hash签名的第i位拿出来，如果为0，则改为-1，如果为1则不变，作为第i个随机向量的第k维。由于hash签名是f位的，因此这样能产生f个随机向量，对应f个随机超平面。

         simhash算法得到的两个签名的汉明距离可以用来衡量原始向量的夹角。这其实是一种降维技术，将高维的向量用较低维度的签名来表征。衡量两个内容相似度，需要计算汉明距离。汉明距离是两个字符串对应位置的不同字符的个数：
     1011101 与1001001 之间的汉明距离是2。