PMBOK第7版
#PMP##职场##项目管理##战略##价值#
2020年1月15日PMBOK ®第7版的征求意见稿发布,并于2020年1月14日结束意见征集,预计于今年第四季度发布。
基于我的项目组合管理(PfMP),项目集管理(PgMP),项目管理(PMP)的培训和研究经验,我个人感觉此次改变并没有太大的实质性变化,有点像车企造车,7系先推出的技术,过段时间下放到5系,再过段时间到3系,本次改版就是将部分原来项目集管理标准(PgMP的考试用书)与项目组合管理标准(PfMP的考试用书)的内容下放了。闲话不多说,下面我来具体说说PMBOK ®第7版的变化。
什么促使PMBOK的改版?
此前版本的PMBOK基本都是维持启动,规划,执行,监控,收尾这样一个五大过程组的瀑布式项目管理。但是,随着我们进入一个VUCA的时代["不稳定"(Volatile)、"不确定"(Uncertain)、"复杂"(Complex)、和"模糊"(Ambiguous)]。这使得产品或项目的需求随时都可能发生变化。
现有的PMBOK体系无法满足快速变化的项目需求。其实早在2000的时候PMI就意识到了这一点当时推出了敏捷项目管理(ACP),敏捷管理近些年在IT与软件开发行业特别盛行。
美国项目管理协会PMI是目前世界最大的项目管理组织,PMP认证又是其旗下最为强势的认证体系,而PMBOK正是PMP认证考试的基石。因此PMBOK每3-5年更新一次以适应项目管理的动态变化与发展。以确保PMBOK作为项目管理届圣经的权威性。
PMBOK第七版中的变化
简单来说PMBOK第七版的变化主要是由之前的注重流程改变为更加注重基本原则。这也就是说PMBOK 第七版更加关注最终的项目成功与否和价值交付。新的标准更加建议项目经理根据自身项目特征,行业,干系人和组织要求等,选择更加适合的管理方法,这些方法可以是敏捷,混合或瀑布式的等而不必局限与某一种。
基于原则管理与基于流程管理的区别
考过PMP的应该都知道ITTO(即输入,工具,技术,输出)也是考试人的恶梦,每个知识领域都有对应的ITTO。好消息是想考PMP的同学,不着急的话等等,等到PMP考试用书改为PMBOK第七版的时候,就不再用死记硬背这些ITTO了,它们在新标准中不再适用。因为PMBOK第七版将秉持注重那些被普遍接受和良好的实践的原则。简单来说就是新PMBOK第七版将关注项目最终向组织及其干系人交付的整体价值,而不在像现在这样仅仅关注项目的产出和可交付物,也就是说项目通过交付成果,再由这些成果给组织和干系人带来价值。不过要知道的是传统的项目管理方法依然有效,并且会在很多传统项目中继续发挥积极作用。
PMBOK第6版与第七版的变化对比
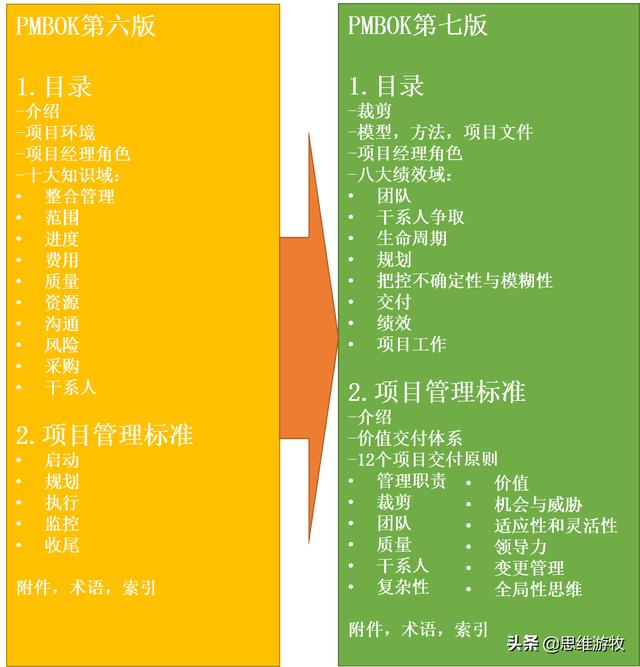
PMBOK第6版与第7版的变化对比
PMBOK 第六版中10大知识领域在PMBOK第七版中,将由8大绩效与领域取代,此外将增加还将有“裁剪,模型,方法和项目文件”章节。
PMBOK第七版中将传统的PMBOK 五大项目管理过程组:启动,规划,执行,监控以及收尾,定义为项目生命周期的五个阶段。每个绩效域,都有属于这些过程组的过程。例如,规划干系人争取是属于规划过程组和干系人争取绩效域的过程。
PMBOK第7版将会从原来的基于过程转变为基于原则。新版本将定义12个项目交付原则和价值交付系统。价值交付系统将专注于交付有价值的成果。在价值交付体系中项目是其基本组成部分,其原则将指导项目经理,团队成员和干系人如何实现预期结果,从而为组织和干系人带来价值。
价值交付体系
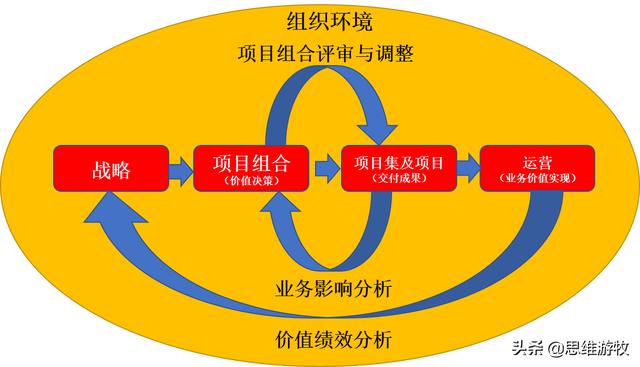
价值交付体系
基于此价值交付体系,我们可以看出组织的战略,使命或目标将决定项目组合的构成。项目组合可以包括子项目组合,项目集或项目。为了实现项目组合的目标,项目集和项目的交付就必须达到项目组合预定的目标。根据项目执行的结果进行业务影响分析,将业务影响分析结果作为评审和调整项目组合的依据。
业务价值实现是指项目不仅需要成功交付,而且还必须为组织创造预期的业务价值。 组织根据已实现的业务价值和已交付项目的成果,再次制定战略,并根据新的战略新的项目组合。
项目团队可以通过使用不同的交付方式来产生预期的结果。因此传统意义上的“项目管理”可能不适用于某些项目,所以在PMBOK第7版中使用“项目交付”代替“项目管理”,以涵盖项目的成果和可交付成果。
项目交付原则
PMBOK第7版将有12条原则,这些原则定义了项目交付的“内容”和“原因”。项目交付原则描述的是基本原理,规范或价值。为了确保项目交付能够预期结果,项目团队成员必须遵循以下12条原则:
1)管理职责:成为勤勉的,懂得尊重和关怀他人的管理者。
2)团队:有担当和懂尊重的团队文化。
3)干系人:做好干系人争取工作并充分了解他们的利益和需求。
4)价值:专注于价值。
5)全局性思维:识别并响应系统性的相互影响。
6)领导力:激励,影响,指导和学习。
7)裁剪:根据不同的项目环境裁剪项目交付方法以制定出最适合的交付交付方法。
8)质量:将质量管理监控融入到各个流程与结果中去。
9)复杂性:使用知识,经验和不断学习来解决复杂性。
10)机遇与威胁:应对机遇与威胁。
11)适应性和灵活性:具有适应性和灵活性。
12)变更管理:通过变更管理是组织最好接受变更的准备,减小变革阻力等以实现预期的收益。
夯实基础:图解项目,项目集,项目组合,运营与组织的关联
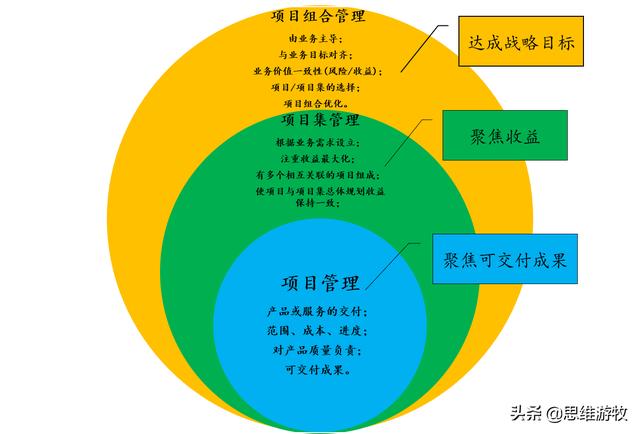
项目,项目集与项目组合管理的关系
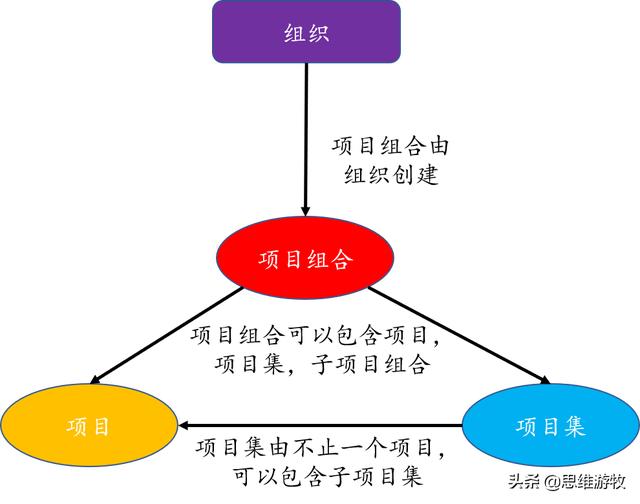
项目,项目集,项目组合,组织之间的关联
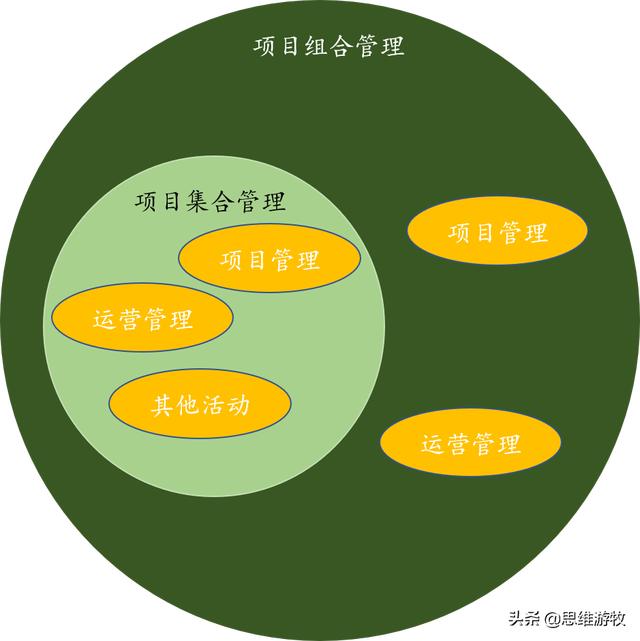
项目,项目集,项目组合与运营的关联
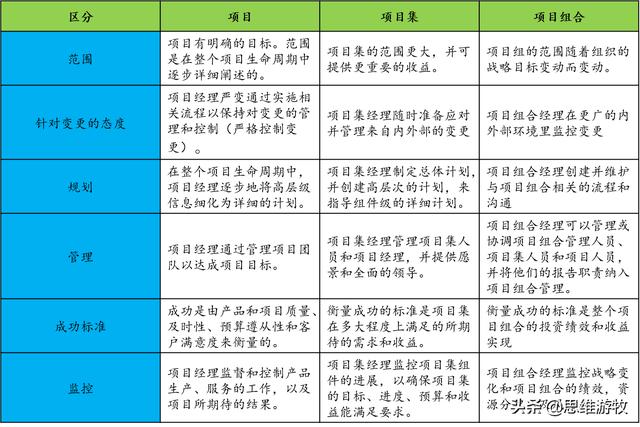
项目,项目集,项目管理之间的区别