
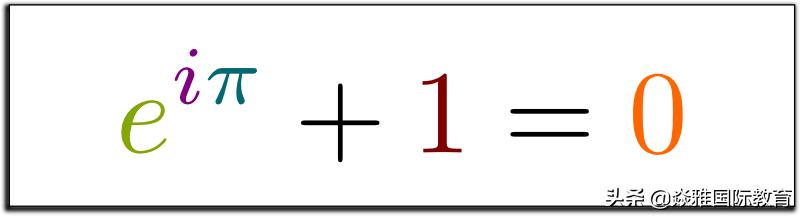
同学们,我们先来跟老师欣赏一下数学中最优美的式子吧?
是什么魔力让以上几个似乎毫不相干的数学中最特殊的数字能如此优美的写在同一个式子呢?
是欧拉,是数学。
0和1——老师就不用介绍啦,
e是自然常数(natural constant),在数学中具有举足轻重的地位,定义为
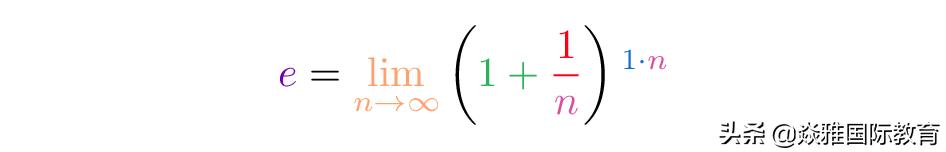
e是一个无理数,意味着其小数点后的数字是随机的不存在什么规律,关于e同学们可以参看老师之前说的文章(我和小e有个“约会”),其大概大小为2.71828,而π大家应该也都很熟悉,同样也是一位无理数,大概为3.14159。i是我们在高数中会学到的,是虚数单位,定义为
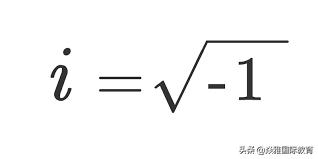
同学们了解完上述的数值后,下面隆重登场今天的“重头戏”:给大家介绍两种巧妙的证明方法,不需要借助泰勒展开(Taylor series),会一点微积分基础的同学都可以明白的。
第一种证明方法
我们先通过一个微分方程(differential equation)来进一步推导出第一种证明方法:
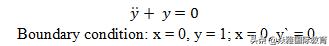
1、微分方程定义:
微分方程是把一个是指含有未知函数及其导数的关系式,物理中的各种公式几乎都是微分方程。
2、推导过程:
首先,我们可以用科学史上最有效的方法来解这个不会的东西,那就是:

常见的多项式、三角函数、指数对数函数、中二阶导数等于负的函数,insight!
余弦函数,y=cosx, y'=-sinx, y''=-cosx
我们也可以验证:
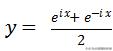
同样也可以符合,
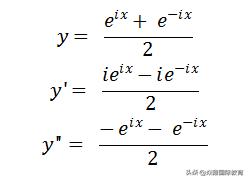
因为微分方程的虚数解只是实数解的另一种表达方法,所以我们可以得到:
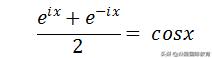
等式两边我们同时求微分,可以得到:
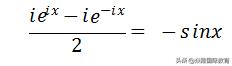
同时乘上-i
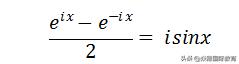
两式相加,我们可以得到:
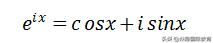
那当x=π的时候,我们就可以得到:
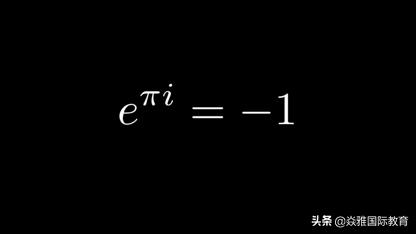
第二种证明方法
我们假设
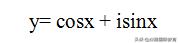
那么对y微分可以得到,
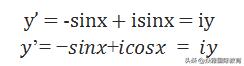
即
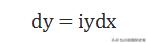
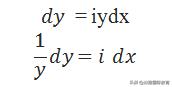
等式两边同时积分,
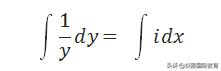
我们可以得到
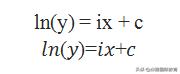
等式两边同时取e^x
我们可以得到
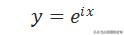
即
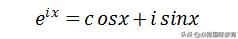
The End
基思•德夫林(Keith Devlin)曾说过:“就像莎士比亚的十四行诗抓住了爱的本质,或者一幅画展现了人类形态的美,远远超出了肤浅的东西,欧拉方程深入到了存在的最深处"。而哈佛大学(Harvard University)教授本杰明·皮尔斯(Benjamin Peirce)在一次演讲中证明了欧拉恒等式后表示"这个恒等式是矛盾的;我们不能理解它,我们不知道它意味着什么,但我们已经证明了它,因此我们知道它一定是真理”。
那么,同学们你们觉得它是美的吗?或许大家有比上述还要好的证明方法,不妨可以和老师一起来探讨研究一下~~
说明:图片来源于网络,如有雷同,请见谅!


...)



。...)


)
)








