1 简介
1.1 横向联邦学习
横向联邦学习也称为按样本划分的联邦学习,主要应用于各个参与方的数据集有相同的特征空间和不同的样本空间的场景,例如两个地区的城市商业银行可能在各自的地区拥有非常不同的客户群体,所以他们的客户交集非常小,并且数据集有不同的样本ID,然而他们的业务模型却非常相似,因此他们的数据集的特征空间是相同的。由此,这两家银行就可以联合起来进行横向联邦学习以构建更好的风控模型。
1.2 相关工作
谷歌联邦学习研发团队在ACM CCS 2017学术大会上提出的一种高效的安全聚合方法,利用秘密共享技术使服务器能够安全地聚合来自不同用户的梯度,同时单个用户的梯度不会被泄露。
Practical secure aggregation for privacy-preserving machine learning
源代码见:https://github.com/ammartahir24/SecureAggregation
2 Practical secure aggregation for privacy-preserving machine learning分析
2.1 论文的动机
机器学习模型通常会包含大量的神经网络参数,而在联邦学习的场景中,用户在本地训练好模型后,需要将这些参数上传至服务器进行聚合,但直接上传是存在隐私泄露的风险的,因此需要将所有参数进行加密再进行聚合。
我们知道加密解密的运算时间是不容忽视的,特别是在训练深度学习神经网络时,模型参数可能达到上千个甚至上万个,对这些模型参数加密并满足同态的性质是一个极具挑战的任务。
2.2 贡献
- (1)支持高维向量的加密;
- (2)即使每一轮有新的用户加入,该方案也能保持高效的通信;
- (3)能够应付用户掉线的情况;
- (4)在以服务器为中介的、未经身份验证的网络模型的约束下提供最强的安全性。
2.3 预备知识
将涉及到秘密共享、密钥协商、认证加密、伪随机数生成、数字签名、公钥基础设施等知识。
2.3.1 Key Agreement 密钥协商
核心为Diffie-Hellman密钥交换,两个用户可以协商一个共享密钥:
- KA.param(k)\operatorname{KA.param} (k)KA.param(k):生成一些公共参数 ppp ppp。
- KA.gen(pp)\operatorname{KA.gen} (p p)KA.gen(pp) :参与方 uuu 根据 ppp ppp 生成私-公密钥对 (suSK,suPK)\left(s_{u}^{S K}, s_{u}^{P K}\right)(suSK,suPK)。
- KA.agree(suSK,svPK)\operatorname{KA.agree} \left(s_{u}^{S K}, s_{v}^{P K}\right)KA.agree(suSK,svPK):用户使用自身的私钥 suSKs_{u}^{S K}suSK 和所有其他用户 vvv 的公钥 svPKs_{v}^{P K}svPK 生成 uuu 和 vvv 之间的私有共享密钥 su,vs_{u, v}su,v 。 在DH密钥协商中使用了哈希函数的密钥协商方案。
2.3.2 Secret Sharing 秘密共享
核心为shamir的(t,n)(t, n)(t,n)秘密分享方案,将要分享的秘密参数sss通过多项式分成nnn份,只有满足至少ttt份份额才可解密得到sss:
- SS.share(s,t,U)\operatorname{SS.share} (s, t, \mathcal{U})SS.share(s,t,U):共享算法,输入为秘密 sss ,代表用户ID的 nnn 个域元素的集合 U\mathcal{U}U ,和一个阈值 t≤∣U∣t \leq|\mathcal{U}|t≤∣U∣ ,输出为共享 sus_{u}su 的集合,其中 u∈Uu \in \mathcal{U}u∈U。
- SS.recon({(u,su)}u∈V,t)\operatorname{SS.recon}\left(\left\{\left(u, s_{u}\right)\right\}_{u \in \mathcal{V}}, t\right)SS.recon({(u,su)}u∈V,t):重构函数,输入为阈值 ttt ,参与共享的用户子集 V⊆U\mathcal{V} \subseteq \mathcal{U}V⊆U 且满足 ∣V∣≥t|\mathcal{V}| \geq t∣V∣≥t ,输出为域元素 sss。
2.3.3 加密、哈希、签名
PRG可以理解为Hash,加密和签名为密码学基本工具。
- 加密:
– AE.enc\operatorname{AE.enc}AE.enc:认证加密的加密算法,输入为密钥key和消息message,输出为密文ciphertext。
– AE.dec\operatorname{AE.dec}AE.dec:认证加密的解密算法,输入为密文ciphertext和密钥key,输出为原始明文或者是错误一个符号。 - 哈希:
– PRG(b)\operatorname{P R G}(b)PRG(b):以 bbb 为随机种子的伪随机数生成算法。 - 签名机制:
– SIG.gen(k)\operatorname{SIG.gen} (k)SIG.gen(k):以安全参数 kkk 作为输入,输出为一个私钥 dSKd^{S K}dSK 和一个公钥 dPKd^{P K}dPK 。
– SIG.sign(dSK,m)\operatorname{SIG.sign} \left(d^{S K}, m\right)SIG.sign(dSK,m):以私钥 dSKd^{S K}dSK 和消息 mmm 作为输入,输出为签名 σ\sigmaσ 。
– SIG.ver(dPK,m,σ)\operatorname{SIG.ver} \left(d^{P K}, m, \sigma\right)SIG.ver(dPK,m,σ) :输入为公钥 dPKd^{P K}dPK ,消息 mmm 和签名 σ\sigmaσ ,验证签名的合法性。
2.4 协议构造
该方案假设用户id有序,且以下算法是以单次聚合的角度进行讨论,但我们知道机器学习需要多次聚合才能收敛到阈值,因此以下讨论的步骤需要在每一次聚合时执行。
2.4.1 加密构思
加密的设计方案如下所示:
yu=xu+∑v∈U:u<vsu,v−∑v∈U:u>vsv,u(modR)\boldsymbol{y}_{u}=\boldsymbol{x}_{u}+\sum_{v \in \mathcal{U}: u<v} \boldsymbol{s}_{u, v}-\sum_{v \in \mathcal{U}: u>v} \boldsymbol{s}_{v, u}(\bmod R) yu=xu+v∈U:u<v∑su,v−v∈U:u>v∑sv,u(modR)
其中su,vs_{u, v}su,v 为用户 uuu 通过与每一个其他用户进行KA.agree(suSK,svPK)\operatorname{KA.agree}( s_{u}^{S K}, s_{v}^{P K} )KA.agree(suSK,svPK) (Key Agreement)得到,若当前用户uuu的id大于vvv的id则加密时相加,否则相减。直观的可以得到,当所有用户上传参数后,这些加密 的参数自然而然能够抵消。
问题1: 这种方法显然存在问题,首先就是巨大的计算和通信开销,为了保证加密参数的随机性,这种 方法需要对每个模型参数都进行一次KA\operatorname{KA}KA协商,那么通信代价为 O(N∗d)\mathbf{O}\left(\mathbf{N}^{*} \mathbf{d}\right)O(N∗d) ,其中N\mathbf{N}N为用户总数, d\mathrm{d}d 为向量 维度(模型参数总数)。
解决方案1: 论文中对加密方式进行了改造,如下所示:
yu=xu+∑v∈U:u<vPRG(su,v)−∑v∈U:u>vPRG(sv,u)(modR)\boldsymbol{y}_{u}=\boldsymbol{x}_{u}+\sum_{v \in \mathcal{U}: u<v} \operatorname{PRG}\left(s_{u, v}\right)-\sum_{v \in \mathcal{U}: u>v} \operatorname{PRG}\left(s_{v, u}\right) \quad(\bmod R) yu=xu+v∈U:u<v∑PRG(su,v)−v∈U:u>v∑PRG(sv,u)(modR)
其中,PRG\operatorname{PRG}PRG就代表哈希,这个式子含义为当所有用户都使用同一个哈希函数并遵循一定的规则,就能实现每一对用户都只需要协商一次KA\operatorname{KA}KA,并将该值哈希 d\mathrm{d}d 次实现加密式子的随机性,便能实现 O(N)\mathbf{O}\left(\mathbf{N}\right)O(N) 的 通信代价。
问题2: 如何解决掉线问题?
解决方案2: 论文使用了shamir大神的秘密共享方案,用户 uuu 将自己的私钥 suSKs_{u}^{S K}suSK 作为 秘密共享参数,把不同的份额分发给其他用户,在聚合阶段若用户 uuu 掉线,那么通过其他至少ttt个用 户便能恢复出密钥。
问题3: 看似已经解决了所有问题,但是考虑这种情况,若用户uuu很晩才将参数上传,但此时服务器判定用 户uuu已经掉线并让其他用户恢复了该用户的私钥,那么此时便能破解用户uuu的参数。考虑更坏的情 况,好奇的服务器可以撒谎用户uuu掉线,这样一来,方案还无法构成足够的安全。
最终方案:
yu=xu+PRG(bu)+∑v∈U:u<vPRG(su,v)−∑v∈U:u>vPRG(sv,u)(modR)\begin{aligned} \boldsymbol{y}_{u}=\boldsymbol{x}_{u} &+\mathbf{P R G}\left(\boldsymbol{b}_{u}\right) \\ &+\sum_{v \in \mathcal{U}: u<v} \operatorname{PRG}\left(s_{u, v}\right) \\ &-\sum_{v \in \mathcal{U}: u>v} \mathbf{P R G}\left(s_{v, u}\right) \quad(\bmod R) \end{aligned} yu=xu+PRG(bu)+v∈U:u<v∑PRG(su,v)−v∈U:u>v∑PRG(sv,u)(modR)
其中bub_{u}bu为用户uuu自行添加的秘密参数,和 sus_{u}su 一样需要将不同的份额分发给其他用户,但是区别就在于 bub_{u}bu是若用户uuu在线才恢复,而sus_{u}su 是用户uuu掉线时恢复,如此一来,一个诚实的用户 vvv便不会同时提交用户uuu的两个秘密份额。
2.4.2 方案具体流程
以用户uuu作为视角作为讨论,其余的用户uuu执行的操作与用户相同。
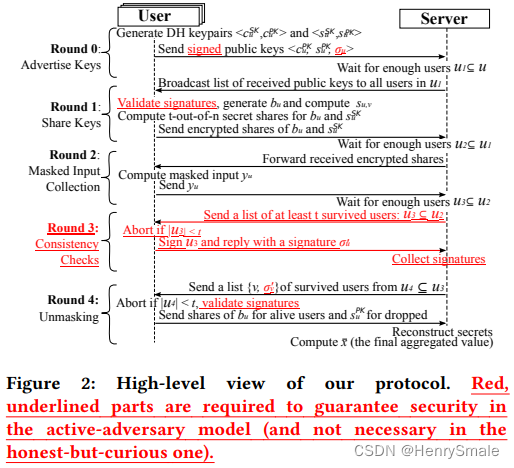
Setup
- 各方都被赋予了安全参数 kkk , 用户数nnn 和一个门限值ttt , honestly generated pp←KA.gen(k)p p \leftarrow \operatorname{KA.gen} (k)pp←KA.gen(k) , 参数mmm和RRR,则 ZRm\mathbb{Z}_{R}^{m}ZRm 是对输入进行采样的空间, 和一个用于秘密分享的字段F\mathbb{F}F 。所有用户还具有与服务器的私有身份验证通道。
- 所有用户 uuu 都会从受信任的第三方收到他们的签名密钥 duSKd_{u}^{SK}duSK,以及绑定到每个用户身份 vvv 的验证密钥 dvPKd_{v}^{P K}dvPK。
Round 0 (AdvertiseKeys)
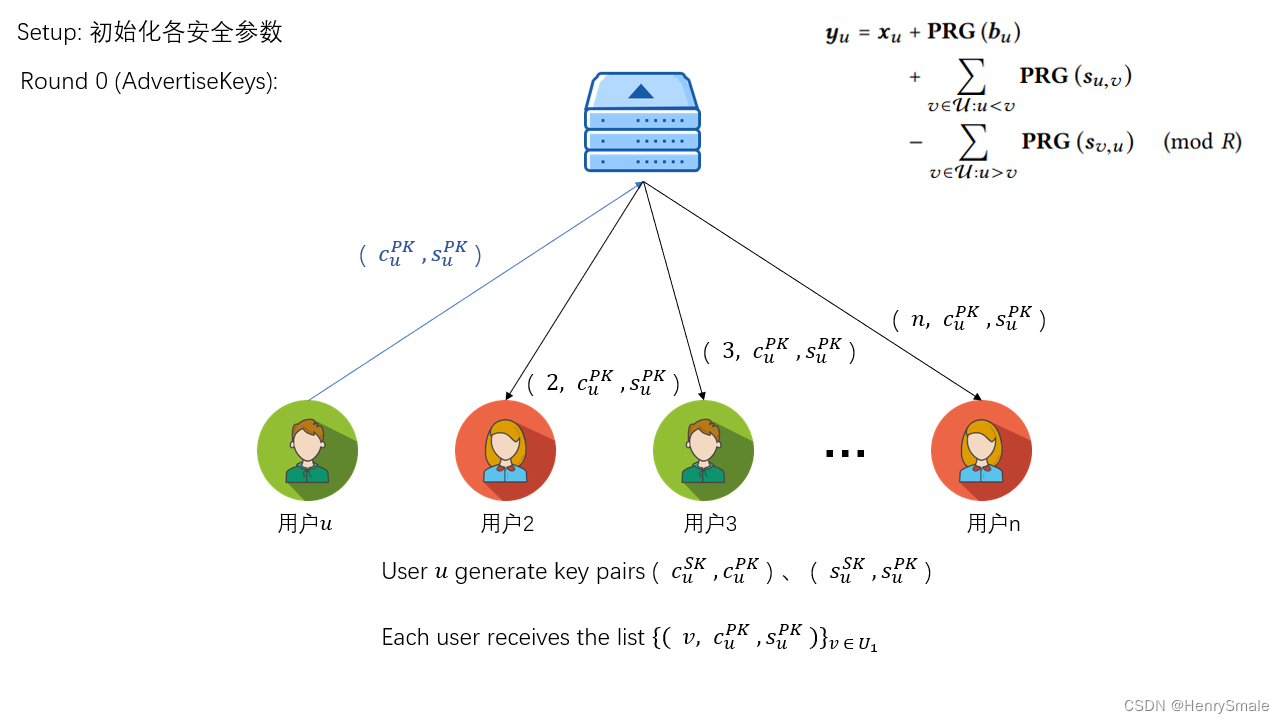
用户uuu:
- 产生密钥对(cuPK,cuSK)←KA⋅gen(pp),(suPK,suSK)←KA⋅gen(pp)\left(c_{u}^{P K}, c_{u}^{S K}\right) \leftarrow \operatorname{KA} \cdot \operatorname{gen}(p p),\left(s_{u}^{P K}, s_{u}^{S K}\right) \leftarrow \operatorname{KA} \cdot \operatorname{gen}(p p)(cuPK,cuSK)←KA⋅gen(pp),(suPK,suSK)←KA⋅gen(pp)以及签名σu←SIG⋅sign(duSK,cuPK∥suPK)\sigma_{u} \leftarrow \operatorname{SIG} \cdot \operatorname{sign}\left(d_{u}^{S K}, c_{u}^{P K} \| s_{u}^{P K}\right)σu←SIG⋅sign(duSK,cuPK∥suPK);
- 将公钥及签名(cuPK∥suPK∥σu)\left(c_{u}^{P K}\left\|s_{u}^{P K}\right\| \sigma_{u}\right)(cuPK∥∥suPK∥∥σu) 发送给服务器,服务器将公钥路由给其他用 户;
- 其他用户拿到用户 uuu 的公钥后与自己的私钥 (cvSK,svSK)\left(c_{v}^{S K}, s_{v}^{S K}\right)(cvSK,svSK) 结合便能得到两个共享密钥: cu,vc_{u, v}cu,v 用来后续加密传输的信息,su,vs_{u, v}su,v 用来加密模型参数。
服务器:
- 从上一轮的个人用户中收集至少 ttt 条消息(用U1\mathcal{U}_{1}U1表示这组用户)。 否则,中止;
- 向 U1\mathcal{U}_{1}U1 列表中的所有用户广播 {(v,cvPK,svPK,σv)}v∈U1\left\{\left(v, c_{v}^{P K}, s_{v}^{P K}, \sigma_{v}\right )\right\}_{v \in \mathcal{U}_{1}}{(v,cvPK,svPK,σv)}v∈U1;
Round 1 (ShareKeys)
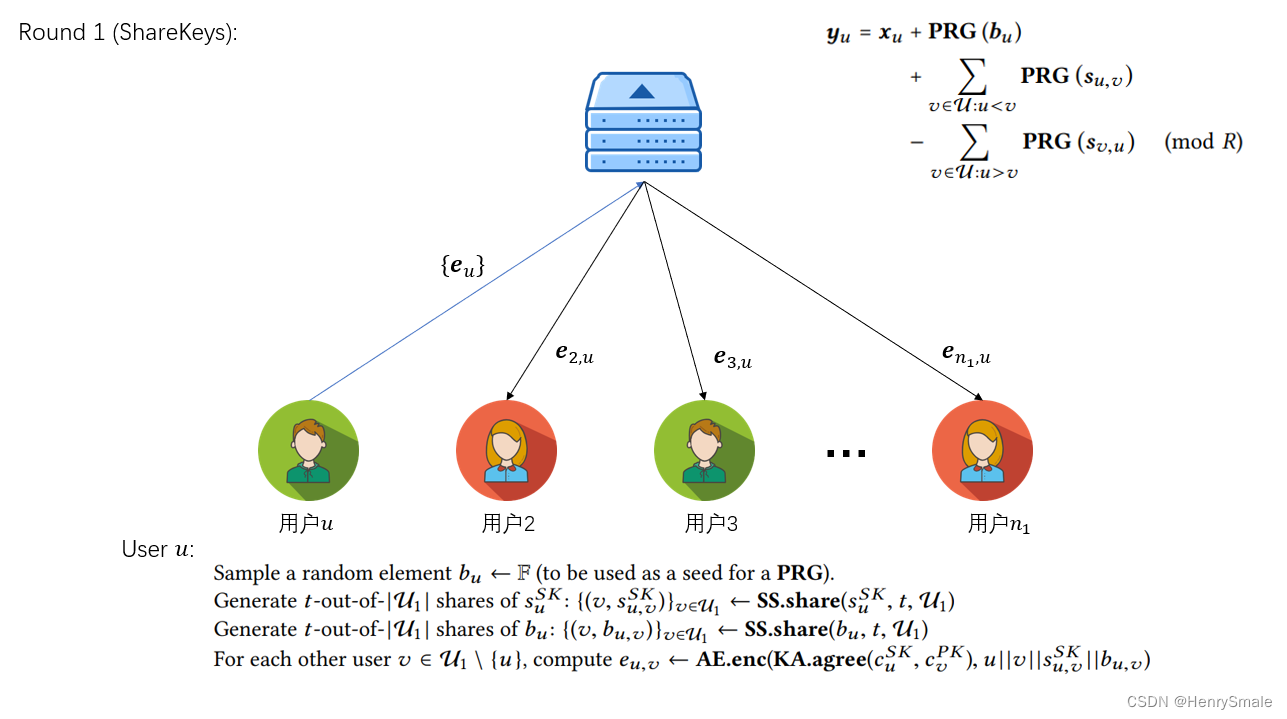
将bub_{u}bu 与 sus_{u}su的秘密份额通过Round 0得到的cu,vc_{u, v}cu,v加密发送给对应的其他用户。
用户uuu:
- 接收由服务器广播得到的列表 {(v,cvPK,svPK,σv)}v∈U1\left\{\left(v, c_{v}^{P K}, s_{v}^{P K}, \sigma_{v}\right)\right\}_{v \in \mathcal{ U}_{1}}{(v,cvPK,svPK,σv)}v∈U1 。 判断以下条件是否满足:∣U1∣≥t\left|\mathcal{U}_{1}\right| \geq t∣U1∣≥t,所有的公钥对都是不同的,并且 ∀v∈U1,SIG.ver(dvPK,cvPK∥svPK,σu)=1\forall v \in \mathcal{U}_{1} , \operatorname{SIG.ver} \left(d_{v}^{PK}, c_{v}^ {P K} \| s_{v}^{P K}, \sigma_{u}\right)=1∀v∈U1,SIG.ver(dvPK,cvPK∥svPK,σu)=1;
- 采样一个随机元素 bu←Fb_{u} \leftarrow \mathbb{F}bu←F(用作 PRG 的种子);
- 生成 t -out-of- ∣U1∣\left|\mathcal{U}_{1}\right|∣U1∣ suSKs_{u}^{SK}suSK 的份额:{(v,su,vSK)}v∈U1←SS.share(suSK,t,U1)\left\{\left(v, s_{u, v}^{SK}\right)\right\}_{v \in \mathcal{U}_{1 }} \leftarrow \operatorname{SS.share}\left(s_{u}^{SK}, t, \mathcal{U}_{1}\right){(v,su,vSK)}v∈U1←SS.share(suSK,t,U1);
- 生成 t -out-of- ∣U1∣\left|\mathcal{U}_{1}\right|∣U1∣ bub_{u}bu 的份额:{(v,bu,v)}v∈U1←SS.share(bu,t,U1)\left\{\left(v, b_{u, v}\right)\right\}_{v \in \mathcal{U}_{1}} \leftarrow \operatorname{SS.share}\left(b_{u}, t, \mathcal{U}_{1}\right){(v,bu,v)}v∈U1←SS.share(bu,t,U1);
- 对于每个其他用户 v∈U1\{u}v \in \mathcal{U}_{1} \backslash\{u\}v∈U1\{u} ,计算 eu,v←AE.enc(KA.agree(cuSK,cvPK),u∥v∥su,vSK∥bu,v)e_{u, v} \leftarrow \operatorname{AE.e n c}\left(\operatorname{KA.agree} \left(c_{u}^{SK}, c_{v}^{PK}\right), u\|v\| s_{u, v}^{SK} \| b_{u, v}\right)eu,v←AE.enc(KA.agree(cuSK,cvPK),u∥v∥su,vSK∥bu,v);
- 如果上述任何操作(断言、签名验证、密钥协商、加密)失败,则中止;
- 将所有密文 eu,ve_{u, v}eu,v 发送到服务器(每个都隐含地包含寻址信息 u,vu, vu,v 作为元数据);
- 存储本轮收到的所有消息和生成的值,然后进入下一轮。
服务器:
- 收集至少 ttt 个用户的密文列表(用 U2⊆U1\mathcal{U}_{2} \subseteq \mathcal{U}_{1}U2⊆U1 这组用户表示);
- 向每个用户 u∈U2u \in \mathcal{U}_{2}u∈U2 发送为其加密的所有密文: {eu,v}v∈U2\left\{e_{u, v}\right\}_{v \in \mathcal{U}_{2} }{eu,v}v∈U2 并进入下一轮。
Round 2 (MaskedInputCollection)
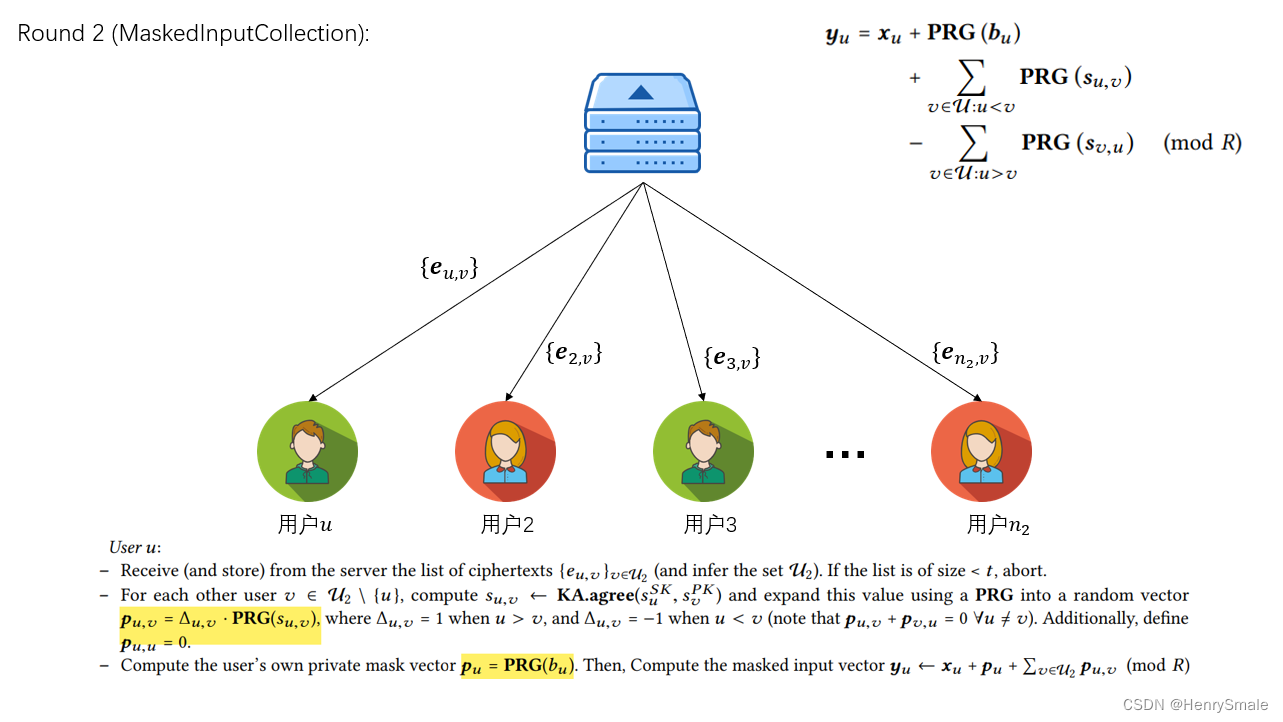
- 从服务端收到其他用户发送给自己的秘密份额后,根据收到的用户列表,计算PRG(su,v)\operatorname{PRG} \left(s_{u, v}\right)PRG(su,v) 和PRG(bu)\operatorname{PRG}( b_{u} )PRG(bu),注意这是每个参数都需要哈希一次,保证每个位置上的参数加密的数都是随机的。
- 计算完成后将加密后的参数上传给服务器。
Round 3
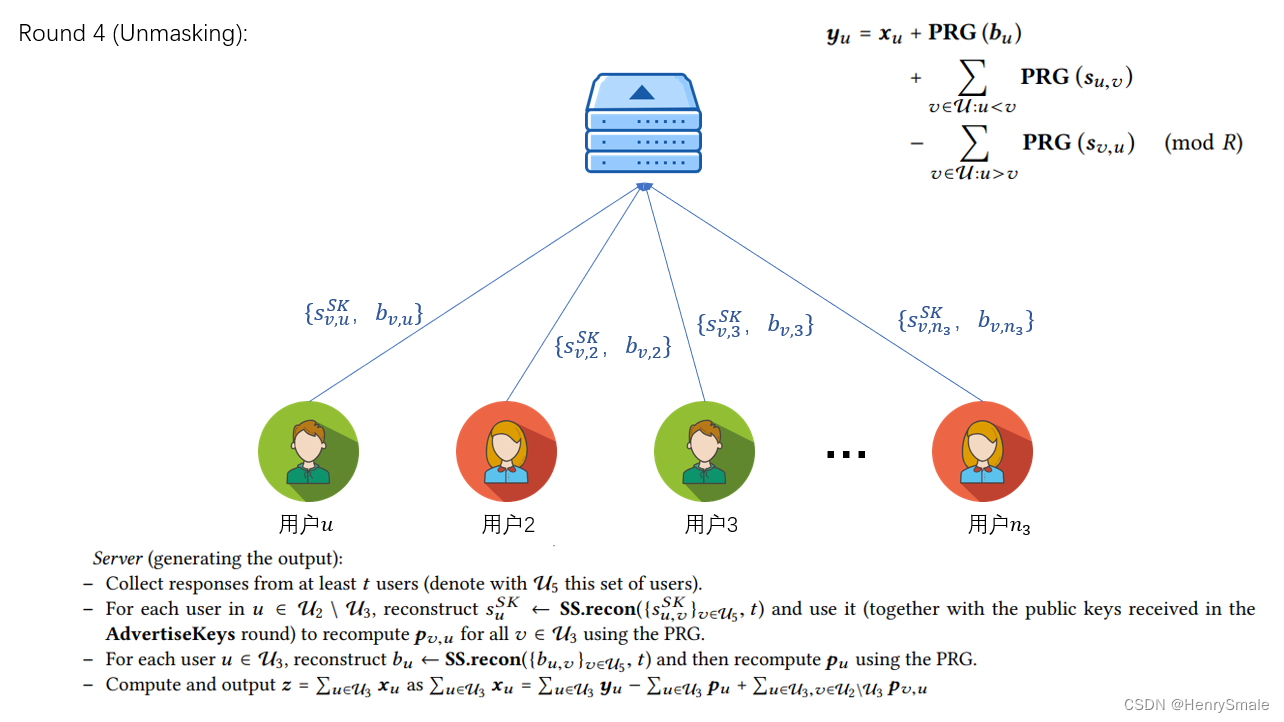
- 服务器将收到的模型参数进行聚合并将掉线用户列表发送给所有用户,用户通过该列表上传掉线用户的秘密份额 sj′s_{j}^{\prime}sj′ 和在线用户的秘密份额 bi′b_{i}^{\prime}bi′;
- 服务器收到至少ttt个用户上传的份额后恢复对应参数,得到聚合结果。
2.4.3 其它
从上述的方案我们可以得知,服务器主要做的路由的作用,完成用户之间信息的交换,因此服务器有能力对不同的用户宣称不同的用户掉线,借此来试图破解shamir秘密共享中的多项式,因此原论文还加了一轮一致性检测,感兴趣的朋友可以去原论文看看~。
参考文献:
内容大部分借鉴了
http://joeybarry.cn/practical-secure-aggregation/

。...)


)
)













:1005.K次取反后最大化的数组和...)