隐私计算 1 隐私计算的定义与背景

1 隐私计算的定义

隐私计算：在保证数据提供方不泄露原始数据的前提下，对数据进行分析计算的一系列技术，保障数据在流通和融合过程中“可用不可见”。

隐私计算涉及到的学科：

密码学；
统计学；
计算机体系结构；
人工智能；
…

两大任务：

数据查询与分析：查询、求和、求平均和方差等简单运算，如何定义数据拥有方的数据隐私并对其进行保护，是该类任务的重要研究课题。
机器学习：利用训练数据，使用最优化方法学习模型，该模型能够学习提取训练数据的特征与共同规律，并利用这些特征和规律对新的数据进行推理分析，从而完成预测、分类和指导行为等任务。如何对训练数据进行隐私保护，以及使用模型对新数据进行推理时，如何对推理数据进行隐私保护，是该类任务的重要研究课题。

2 隐私计算分类

保护的对象：

数据中直观的、有价值的个人隐私，如用户的身份证号码、手机号码和信用卡号码等；
计算任务的运算中间数据与结果，如机器学习训练过程中产生的训练梯度信息与训练完成的模型参数；
计算任务使用的程序或模型，例如实现关键计算任务的函数、过程及SQL语句等。

中文名称	英文名称	定义
隐私计算	Privacy Computing	狭义：以密码学工具为核心的加密计算。广义：保护数据隐私的同时实现计算任务所使用的一系列技术的统称
隐私保护计算	Privacy-perserving Computing	计算前：对数据的安全获取和管理；计算中：对数据隐私的保护和度量；计算后：对生成数据隐私的保护及相关权属与收益分配的一系列技术
安全多方计算	Secure Multi-party Computing	使用密码学工具在安全协议层次构建隐私计算协议，从而实现多个数据拥有者协同完成指定的计算函数，同时不暴露任何其他的隐私信息
秘密共享	Secure Sharing	将隐私数据拆分成多个份额进行分发和计算的加密计算工具。是隐私加密计算的主要实现方案之一。只有获得一定数量的参与方的同意，才能恢复出原始数据
同态加密	Homomorphic Encryption	允许在密文上进行运算的加密方案。在对数据进行加密之后，能够进行运算获得密文结果，只有密钥持有方才能解密查看结果。是加密计算的常用工具
不经意传输	Oblivious Transfer	带隐私保护的数据传输模型。保证发送方将某条隐私数据发送给接收方，发送方不知道接收方的选择，接收方也不知道发送方的其他隐私数据
混淆电路	Garbled Circuit	通过对逻辑门的输入信号和输出信号进行加密来保护电路的明文信号，是适用性最广的隐私加密技术之一
差分隐私	Differential Privacy	一种灵活高效的隐私保护技术。与密码学方案不同，差分隐私并不对数据进行加密，而是以在数据中加入随机噪声的方式对数据进行保护
可信执行环境	Trusted Execution Environment	在硬件层面提供隐私计算的解决方案。可信执行环境提供一个将用户的程序和数据隔离起来的运行环境，使用户的程序代码和数据不会被潜在的攻击者窃取或者篡改
联邦学习	Federated Learning	在机器学习领域提出的一种隐私保护计算方案。在训练的过程中，训练模型所必需的信息在各参与方之间传递，但数据不能传递。联邦学习可以使用保护隐私的技术，如同态加密等，对传输的信息进一步进行保护

3 隐私计算的发展历程

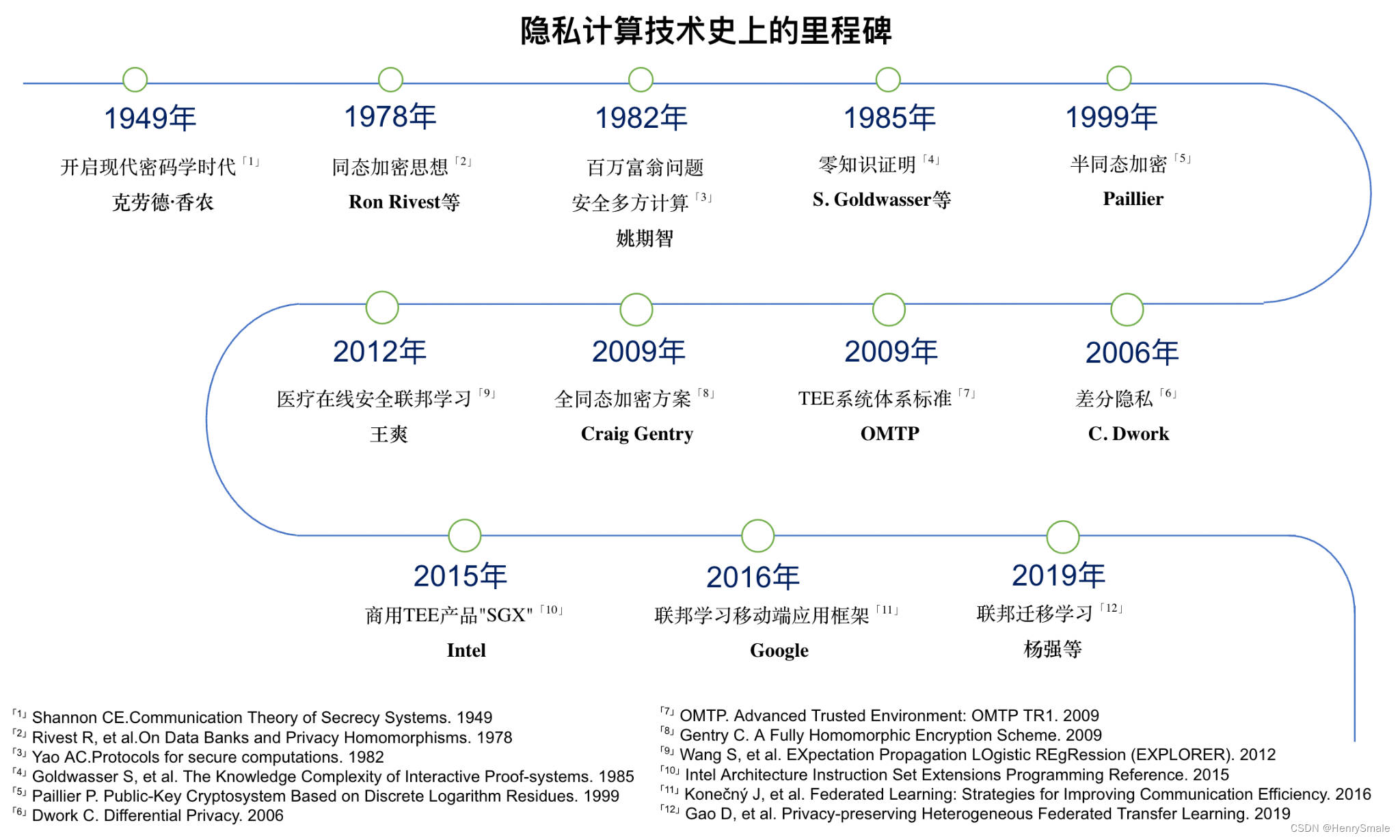
在这里插入图片描述

3.1 萌芽期（1949年-1982年）

20世纪40年代，现代信息学之父克劳德·香农在备忘录《密码学的一个数学理论》的基础上，发表一篇重要论文《保密系统的通信理论》(1)，被认为是开启了现代密码学时代。
1976年，Whitfield Diffie和Martin Hellman共同发表学术论文《New Direction in Cryptography》(2)，创建了公钥加密体制，是现代密码学的里程碑。
1977年，Ron Rivest、Adi Shamir和Leonard Adleman发明非对称式加密算法RSA，突破了长期以来的瓶颈，达到了新的阶段(3)。
1978年，Ron Rivest、Leonard Adleman和Michael L. Dertouzos提出同态加密问题(4)，并在当年提出了满足同态属性的算法，但是并未有完全解决其安全性问题。同态加密问题的提出将加密技术的研究从静态引向动态，是理论上的巨大革新，也开创了隐私计算的先河。
1979年，秘密分享（Secret Sharing, SS）最早由Shamir(5)和Blakley(6)提出。
1981年，不经意传输（Oblivious Transfer, OT）由Rabin首次提出(7)。
1982年，姚期智教授在论文《Protocols for Secure Computations》中提出了“百万富翁问题”，开创性地引入了安全多方计算概念(8)。
Tips：这个阶段，出现了许多划时代的里程碑，不仅仅是香农开启了现代密码学时代，更包括同态加密、多方安全计算等主流技术先后被提出，为日后隐私计算的高速发展与应用奠定了坚实的基础。

3.2 探索期（1983年-1999年）

1985年，S. Goldwasser、S. Micali和C. Rackoff首次提出零知识证明（Zero-Knowledge Proof, ZKP）概念(9)。其目的是解决如下问题：证明者如何向验证者证明自己拥有某一特定的数据，但证明过程不能透露任何有关该数据的信息。
1986年，姚期智教授提出混淆电路（Garbled Circuit, GC）技术，实现了第一个多方（两方）安全计算方案(10)。
1987年，Goldreich等人提出了基于电路的秘密共享方案GMW，并将其应用于多方安全计算(11)。
1996年，Cheung首次提出在分布式数据库中，实现关联规则（Association Rules）挖掘，奠定联邦学习的一些基础概念(12)。
1999年，Paillier在欧密会（EUROCRYPT）上首次提出支持加法同态的公钥密码系统(13)。
Tips：这个阶段，混淆电路、基于秘密分享的MPC、半同态加密等协议和算法陆续出现，此外，零知识证明被提出，联邦学习也开始露出雏形，在即将登场的下一个阶段，联邦学习将闪烁出熠熠光辉。

3.3 成长期（2000年-2018年）

2006年，C. Dwork提出差分隐私（Differential Privacy, DP）(14)，通过引入噪声对数据进行扰动，并要求输出结果对数据集中的任意一条记录的修改不敏感，使攻击者无法根据背景知识推断出敏感信息。
2009年，OMTP工作组率先提出一种双系统解决方案(15)，即在同一个智能终端下，除多媒体操作系统外再提供一个隔离的安全操作系统，这一运行在隔离硬件之上的隔离安全操作系统用来专门处理敏感信息以保证信息安全，该方案是可信执行环境（Trusted Execution Environment, TEE）的前身。
2009年，Craig Gentry提出了首个全同态加密方案（Fully Homomorphic Encryption, FHE）(16)，同时支持密文下的加法和乘法运算，标志着全同态计算时代的开始，并逐渐发展出多种不同的全同态加密方案。其后Paillier，Gentry，王爽等人牵头成立国际同态加密标准委员会，标志着同态加密在全球进入高速发展阶段。
2013年，王爽教授团队在SCI学术期刊Journal of Biomedical Informatics发表《Expectation Propagation Logistic Regression (EXPLORER): Distributed privacy-preserving online model learning》论文 (17)，提出了数据“可用不可见”问题。首次解决医疗在线安全联邦学习问题，该框架服务于多个国家级医疗健康网络，也是联邦学习系统构架层面的突破。
2015年Intel推出商用TEE方案“英特尔软件防护扩展”（Intel Software Guard Extensions, Intel SGX）(18)。
2016年，Google AI团队提出联邦学习算法框架应用于移动互联网手机终端的隐私保护(19)。
2019年，杨强教授团队提出联邦迁移学习，结合联邦学习和迁移学习并发布FATE开源系统(20)。
Tips：这个阶段是隐私计算技术的快速成长期，可谓星光灿烂。在技术创新上，推出首个全同态加密方案，首个医疗在线安全联邦学习底层框架，还包括TEE方案框架的提出与落地。

3.4 应用期（2019年至今）

2019年至今，在数据要素市场建设和数据价值发挥的时代背景下，产业需求快速增长，隐私计算走出学院派与实验室，广泛与行业应用场景相结合，赋能数据价值的安全、合规流转，各类隐私计算厂商也如雨后春笋一般涌现出来，激发了隐私计算技术可用性的快速提升。
当前，隐私计算仍处于产业快速导入期，即将迈入“隐私计算+”时代。未来，隐私计算将如同移动互联网、水、电网一般，成为数字时代的底层基础设施。

4 秘密共享算法分类

秘密共享算法大致可以分为十类：

阈值秘密共享方案：
– Shamir-Blakley方案
– 基于中国剩余定理的Asmuth-Bloom方法
– 使用矩阵乘法的Karnin-Greece-Hellman方法
一般访问结构上秘密共享方案：单调电路构造法等
多重秘密共享方案
多秘密共享方案
可验证共享方案
动态秘密共享方案
量子秘密共享方案
可视秘密共享方案
基于多分辨滤波的秘密共享方案
基于广义自缩序列的秘密共享方案

5 经典秘密共享方案

介绍四种经典的秘密共享方案：Shamir、基于中国剩余定理、Brickell、Blakley。

参考文献

Shannon CE. Communication theory of secrecy systems. The Bell System Technical Journal. 1949 Oct;28(4):656–715.
Diffie W, Hellman M. New directions in cryptography. IEEE Trans Inf Theory. 1976 Nov;22(6):644–54.
Calderbank. The rsa cryptosystem: history, algorithm, primes. Chicago: math uchicago edu [Internet]. Available from: http://math.uchicago.edu/~may/VIGRE/VIGRE2007/REUPapers/INCOMING/REU%20paper.pdf
Rivest RL, Adleman L, Dertouzos ML. On data banks and privacy homomorphisms. Foundations of secure [Internet]. 1978; Available from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.500.3989&rep=rep1&type=pdf
Shamir A. How to share a secret. Commun ACM. 1979 Nov;22(11):612–3.
Blakley. Safeguarding cryptographic keys. In: Managing Requirements Knowledge, International Workshop on. 1979. p. 313.
Rabin MO. How To Exchange Secrets with Oblivious Transfer. Cryptology ePrint Archive [Internet]. 2005 [cited 2022 May 28]; Available from: https://eprint.iacr.org/2005/187
Yao AC. Protocols for secure computations. In: 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982). 1982. p. 160–4.
Goldwasser S, Micali S, Rackoff C. The knowledge complexity of interactive proof-systems [Internet]. Proceedings of the seventeenth annual ACM symposium on Theory of computing – STOC ’85. 1985. Available from: http://dx.doi.org/10.1145/22145.22178
Yao ACC. How to generate and exchange secrets. In: 27th Annual Symposium on Foundations of Computer Science (sfcs 1986). 1986. p. 162–7.
Goldreich O, Micali S, Wigderson A. How to Play ANY Mental Game. In: Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing. New York, NY, USA: ACM; 1987. p. 218–29. (STOC ’87).
Cheung DW, Han J, Ng VT, Fu AW, Fu Y. A fast distributed algorithm for mining association rules. In: Fourth International Conference on Parallel and Distributed Information Systems. 1996. p. 31–42.
Paillier P. Public-Key Cryptosystem Based on Discrete Logarithm Residues. EUROCRYPT 1999 [Internet]. 1999 [cited 2022 May 28]; Available from: https://ci.nii.ac.jp/naid/10021850608/
Dwork C. Differential Privacy. In: Automata, Languages and Programming. Springer Berlin Heidelberg; 2006. p. 1–12.
Hardware Working Group. ADVANCED TRUSTED ENVIRONMENT: OMTP TR1 [Internet]. OMTP Limited; 2009. Available from: https://www.gsma.com/newsroom/wp-content/uploads/2012/03/omtpadvancedtrustedenvironmentomtptr1v11.pdf
Gentry C. A fully homomorphic encryption scheme [Internet]. 2009. Available from: https://search.proquest.com/openview/93369e65682e50979432340f1fdae44e/1?pq-origsite=gscholar&cbl=18750
Wang S, Jiang X, Wu Y, Cui L, Cheng S, Ohno-Machado L. EXpectation Propagation LOgistic REgRession (EXPLORER): distributed privacy-preserving online model learning. J Biomed Inform. 2013 Jun;46(3):480–96.
Intel. Intel Architecture Instruction Set Extensions Programming Reference [Internet]. Intel; 2015. Available from: https://www.intel.com/content/www/us/en/developer/overview.html#page=36
Konečný J, Brendan McMahan H, Yu FX, Richtárik P, Suresh AT, Bacon D. Federated Learning: Strategies for Improving Communication Efficiency [Internet]. arXiv [cs.LG]. 2016. Available from: http://arxiv.org/abs/1610.05492
Gao D, Liu Y, Huang A, Ju C, Yu H, Yang Q. Privacy-preserving Heterogeneous Federated Transfer Learning. In: 2019 IEEE International Conference on Big Data (Big Data). 2019. p. 2552–9.
http://prnews.techweb.com.cn/qiyenews/archives/321251.html
李凤华, 李晖, 牛犇. 隐私计算理论与技术
中国移动通信联合会, 中科院信工所, 中国信通院. 2021隐私机密计算蓝皮书
交通银行. 隐私计算金融应用蓝皮书
中国信通院. 联邦学习场景应用研究报告（2022年）
北京金融科技产业联盟. 隐私计算技术金融应用研究报告
中国移动. 隐私计算应用白皮书（2021）
微众银行, 毕马威. 2021隐私计算行业研究报告：深潜数据蓝海
艾瑞咨询. 2022年中国隐私计算行业研究报告