算法的重要性，我就不多说了吧，想去大厂，就必须要经过基础知识和业务逻辑面试+算法面试。所以，为了提高大家的算法能力，这个公众号后续每天带大家做一道算法题，题目就从LeetCode上面选 ！

今天和大家聊的问题叫做 子集 II，我们先来看题面：

https://leetcode-cn.com/problems/subsets-ii/

Given a collection of integers that might contain duplicates, nums, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

题意

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集(幂集)。说明：解集不能包含重复的子集。样例

输入: [1,2,2]
输出:[
  [2],[1],[1,2,2],[2,2],[1,2],[]
]

解题

https://www.cnblogs.com/techflow/p/13489811.html

题解

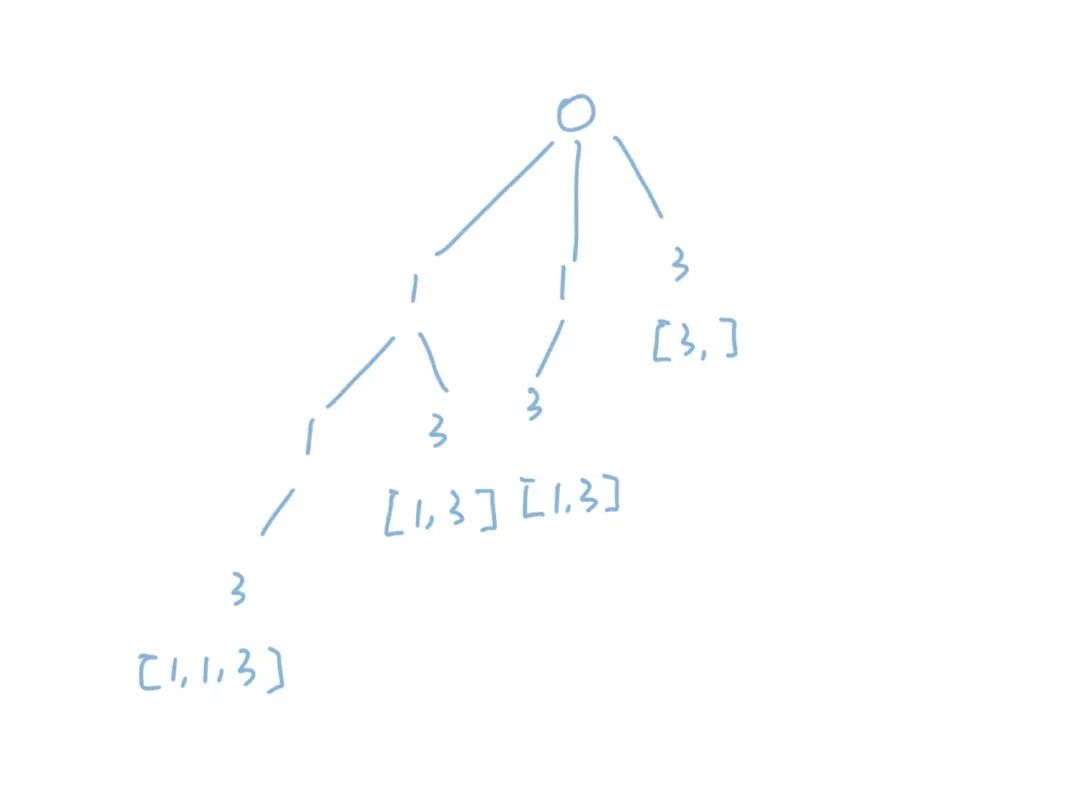
全排列的问题也好，获取子集也好，这些问题都已经算是老生常谈了，我们之前做过不少。这些问题经过转化之后，本质上还是搜索问题。我们在样本空间当中搜索所有合法的解，存储起来。这道题的前身LeetCode78题用的正解也是搜索的解法，对于使用搜索算法来解这道题问题不大，但问题是针对数组当中的重复元素我们应该怎么样来处理。最简单也是最容易想到的方法当然是先把所有的子集全部找到之后，我们再进行去重。如果采用这样的方法，还有一个便利是我们可以不用递归，而是可以通过二进制枚举的方法获取所有的子集。但也有一个问题，问题就是复杂度。我们把集合当中的每一个数字都看成是独立的，那么对于每一个数字来说都有取和不取两种方案。对于n个数字来说，方案总数当然就是。并且我们还需要对这个集合进行去重，这带来的开销可想而知。当然针对这个问题我们也有解决方案比如可以用hash算法将一个集合hash成一个数，如果hash值一样说明集合的构成相同。这样我们就可以通过对数字去重来实现集合去重了。但这样仍然不是完美的，首先hash算法也不是百分百可靠的，也可能会出现hash值碰撞的情况。其次，这种方案的实现复杂度也很大，我们找出所有集合之后再通过hash算法进行过滤，整个过程非常麻烦。很明显，这题一定还存在更好的方法。既然事后找补不靠谱，那么我们可以试着事前避免。也就是说我们在搜索所有子集的时候就设计一种机制可以过滤掉重复的集合或者是保证重复的集合不会出现。我们可以分析一下重复的集合出现的原因，两个集合完全一样，说明其中的元素构成完全一致。元素的构成一致又有两种可能，第一种是重复的获取，比如[1, 3]，我们先拿1再拿3和先拿3再拿1本质上是一样的。还有一种可能是元素的重复导致的集合重复，比如[1, 3]假如我们候选的1不止一个，那么拿不同的1也会被认为是不同的方案。针对第一种情况出现的重复非常简单，我们可以对元素进行排序，之后限定拿取元素的顺序。只能从左拿到右，不能先拿右边的元素再回头拿左边的元素，这样就禁止了第一种情况导致的重复。这个方法我们曾经在很多问题当中用到过，就不详细介绍了。下面来说说第二种情况，就是重复元素导致的重复集合。这一点需要结合代码来仔细说明，我们来看一段经典的搜索代码：

def dfs(cur, subset):    for i in range(cur, n):
        nxt = subset + [nums[i]]
        ret.append(nxt)
        dfs(i+1, nxt)

这一段是一个经典的搜索代码，我们在for循环当中执行的其实是一个枚举操作，也就是枚举这一轮我们要拿取哪一个元素。这里我们限制了选择的范围只能在上一次选择元素的右侧，也就是上文当中说的针对第一种情况的方案。假设我们当前候选的元素是[1, 1, 3, 3]，这里虽然有4个元素，但是值得我们搜索的其实只有两个，就是1和3。因为第二个1和第二个3都没有任何用处，只会导致结果重复。并且假设我们希望得到[1, 1]这样的结果，只能通过拿取左侧的1实现。也就是说如果出现重复的元素，我们只需要考虑第一个出现的，其余都没有考虑的必要。为了更加形象， 我们画出这一段的搜索树。这里我们为了简化图示，只画了[1, 1, 3]三个数的情况。可以看出我们选第一个1和第二个1，都构建出了[1, 3]这个集合，这是重复的。并且我们可以发现第二个1的所有情况第一个1都已经包括了，所以这一整个分支都是多余的，可以剪掉。

最后，我们把上面的细节全部串起来写出代码：

class Solution:def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:# 对元素排序，将重复的元素挨在一起
        nums = sorted(nums)
        ret = [[]]
        n = len(nums)def dfs(cur, subset):    # 上一次选择的元素，一开始置为None
            last = Nonefor i in range(cur, n):if i == cur or nums[i] != last:# 存储集合
                    nxt = subset + [nums[i]]
                    ret.append(nxt)# 更新last
                    last = nums[i]
                    dfs(i+1, nxt)
        dfs(0, [])return ret

到这里，我们关于这道题的介绍就结束了。从代码上来看，这道题的代码不长，涉及到需要推理的细节也并不多，总体的难度并不大。但作为一道搜索问题，它仍然非常有价值。如果你能自己思考推导得出正确的递归代码，那么说明你对递归的理解已经可以算是合格了，所以这题也非常适合面试，要准备找工作的小伙伴，可以仔细刷刷。好了，今天的文章就到这里，如果觉得有所收获，请顺手点个在看或者转发吧，你们的支持是我最大的动力。

上期推文：

LeetCode50-80题汇总，速度收藏！LeetCode刷题实战81：搜索旋转排序数组 IILeetCode刷题实战82：删除排序链表中的重复元素 IILeetCode刷题实战83：删除排序链表中的重复元素LeetCode刷题实战84： 柱状图中最大的矩形LeetCode刷题实战85：最大矩形LeetCode刷题实战86：分隔链表LeetCode刷题实战87：扰乱字符串LeetCode刷题实战88：合并两个有序数组LeetCode刷题实战89：格雷编码