
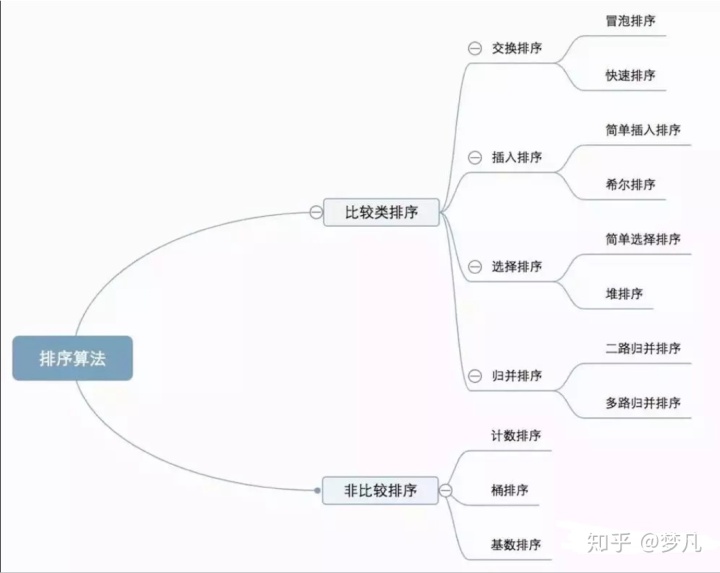
排序算法作为数据结构的重要部分,系统地学习一下是很有必要的。
十种常见排序算法可以分为两大类:
比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
全部排序代码整理:
链接:https://pan.baidu.com/s/1c02Nfm8PjXg0PQtFRv6F1A
提取码:rjnq
1、冒泡排序
它重复地走访过要排序的元素列,依次比较两个相邻的元素
- 动图演示
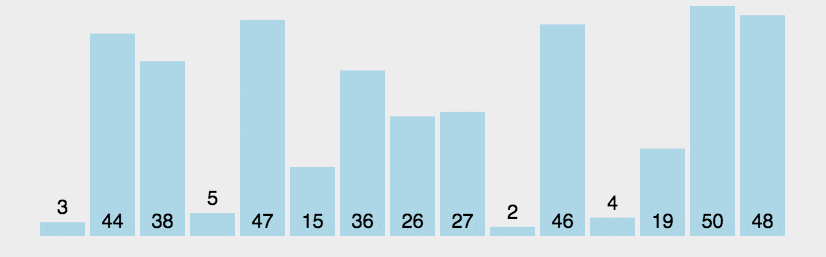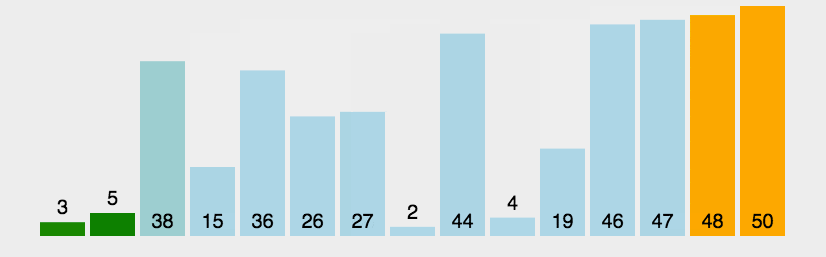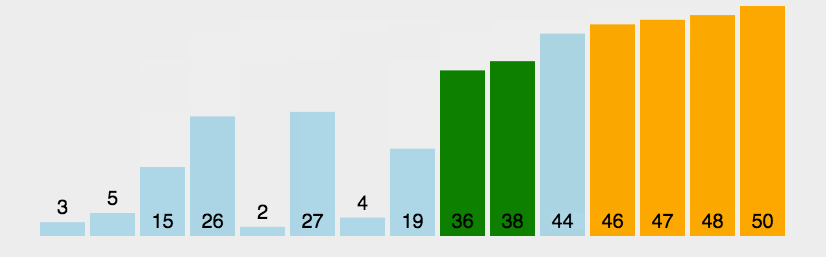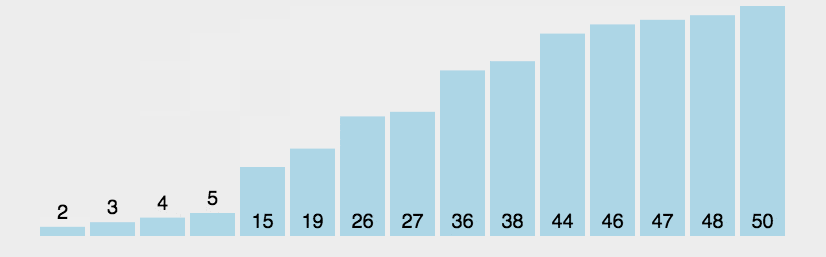
- 代码实现
void 2、选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
- 动图演示
- 代码实现
void SelectSort(int arr[], int n)
{for (int i = 0; i < n - 1; i++){for (int j = i + 1; j < n; j++){if (arr[i] > arr[j]){swap(arr, i, j); //交换arr数组arr[i]和arr[j]的值}}}
}3、插入排序
插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据
- 动图演示
- 代码实现
void InsertSort(int arr[], int n)
{int tempVal;for (int i = 1, j; i < n; i++){tempVal = arr[i]; //保存要插入的值for (j = i - 1; tempVal < arr[j] && j >= 0; --j) //数据往后移动,给要插入的值腾位{arr[j + 1] = arr[j];}arr[j + 1] = tempVal; //插入数据}
}4、快速排序
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
- 动图演示
- 代码实现
void Quicksort(int a[], int low, int high)
{if (low >= high){return;}int first = low;int last = high;int key = a[first];while (first<last){while (first < last && a[last] >= key) //从右往左找一个比arr[left]小的值{--last;}a[first] = a[last];while (first < last && a[first] <= key) //从左往右找一个比arr[left]要大的值{++first;}a[last] = a[first];}a[first] = key;Quicksort(a, low, first - 1); //排左边Quicksort(a, last + 1, high); //排右边
}5、希尔排序
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。插入排序是将未排序的数字插入到已排序数列中,而希尔排序是将一个已排序的数列插入到另一个已排序的数列中。
- 图片演示
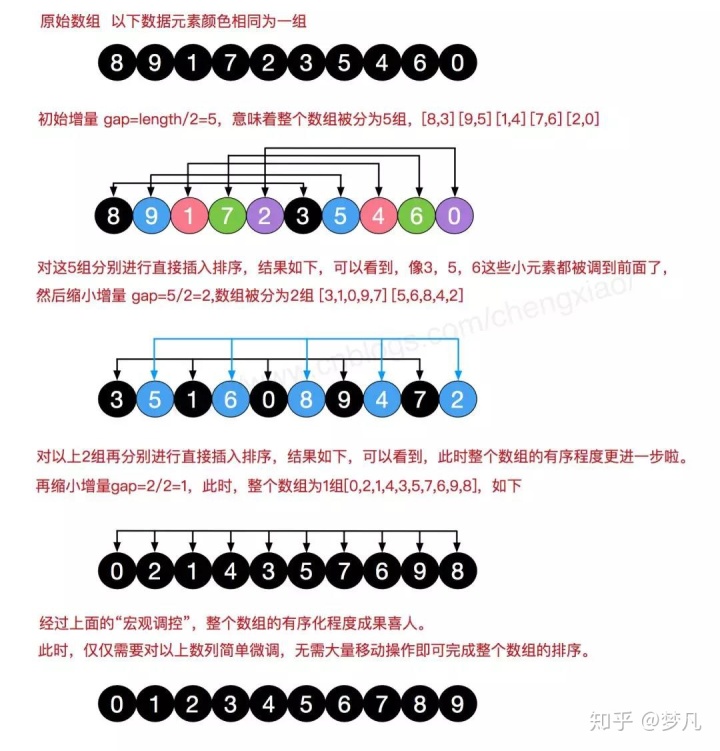
- 代码实现
void ShellSort(int arr[], int n)
{int tempVal, j;int jump = n >> 2; //步长值while (jump != 0){for (int i = jump; i < n; i++){tempVal = arr[i]; //保存待排序的第一个数,也就是待插入的数for (j = i - jump; j >= 0 && tempVal < arr[j]; j -= jump){arr[j + jump] = arr[j];}arr[j + jump] = tempVal;}jump = jump >> 1; //步长值减半}
}6、归并排序
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表
- 动图演示
- 代码实现
void MergeSort(int arr[], int left, int right)
{if (left >= right)//递归的终止条件,left == right证明这个区间只有一个元素,不需要再拆了return;int mid = ((right - left) >> 1) + left;//求中点MergeSort(arr, left, mid); //拆分左MergeSort(arr, mid + 1, right); //拆分右//并操作_merge_in_arr(arr, left, mid, right);
}void _merge_in_arr(int arr[], int left, int mid, int right)
{int length = right - left + 1; //定义一个辅助的空间的长度int *pData = (int*)malloc(sizeof(int)*length);//分配一个动态内存来调整元素的位置memset(pData, 0, sizeof(int)* length);//合并int low = left; //左边区间的起始下标int hig = mid + 1; //右边区间的起始下标int index = 0; //辅助数组的下标while (hig <= right)//右区间没有合并完{while (low <= mid && arr[low] <= arr[hig])//证明左区间没有合并完,且左区间的值小于右区间的值{pData[index] = arr[low]; //把左边的值放进辅助数组low++; //左边往高位移,下一次需要判断左边的新下标index++; //下一次放进辅助数组的新下标}if (low > mid) //证明左区间已经放完break;while (hig <= right && arr[low] > arr[hig])//证明右区间没有合并完,且左区间的值大于右区间的值{pData[index] = arr[hig]; //把右边的值放进辅助数组hig++; //右边往高位移,下一次需要判断右边的新下标index++; //下一次放进辅助数组的新下标}}//到这一步,证明起码有一个区间已经合并完成if (hig <= right) //证明右边没有完成memmove(&pData[index], &arr[hig], sizeof(int)* (right - hig + 1));if (low <= mid) //证明左边没有完成memmove(&pData[index], &arr[low], sizeof(int)* (mid - low + 1));//把所有区间都合并到了辅助区间memmove(&arr[left], pData, sizeof(int)* length);free(pData); //释放空间
}7、桶(基数)排序
桶排序是典型的空间换时间,在对整数排序中,没有什么算法能比它还快,但是在空间浪费上,它是祖宗。
- 动图演示

- 代码实现
void radix_sort(int arr[], size_t len)
{int**temp = (int **)malloc(sizeof(int) * 10); //10行//申请动态内存 辅助数组temp[10][];for (int i = 0; i < 10; i++){temp[i] = (int *)malloc(sizeof(int)*len);}for (int i = 1; i <= 100; i *= 10)//循环数值可能有的位数{for (int x = 0; x < 10; ++x)//辅助数组行循环{for (int y = 0; y < len; ++y)//辅助数组列循环{temp[x][y] = -1;//辅助数组的初始化赋值,-1表示在arr里面不可能出现的数值 }}//arr数组中的元素放入辅助数组for (int m = 0; m < len; ++m){int index = (arr[m] / i) % 10;temp[index][m] = arr[m];}//把辅助数组的内容放回待排序数组int k = 0;//待排序的下标for (int x = 0; x < 10; x++){for (int y = 0; y < len; ++y){if (temp[x][y] != -1)arr[k++] = temp[x][y];}}}//释放内存for (int i = 0; i < 10; i++){free(temp[i]);}free(temp);
}在这里我列举了7中常见的排序算法并用C语言实现,你们可能就要问了,不是十种吗?怎么还能缺斤短两,不是我不会写啊,是写起来麻烦,你们也用不到后面那几种,跟别说去研究了,能看懂常见的七种排序算法你就能在学校里横着走了。
编辑:梦凡
微信公众号:编程学习基地








![webservice 实现与his系统对接_[Share] EDI 及其他常见系统对接技术](http://pic.xiahunao.cn/webservice 实现与his系统对接_[Share] EDI 及其他常见系统对接技术)


)


)


—— 浏览器安全)

