前言

这篇文章是基于B站王道考研的教程写的。
文章图片会有不少引用课程ppt。

以下思维导图概括了本文的内容。

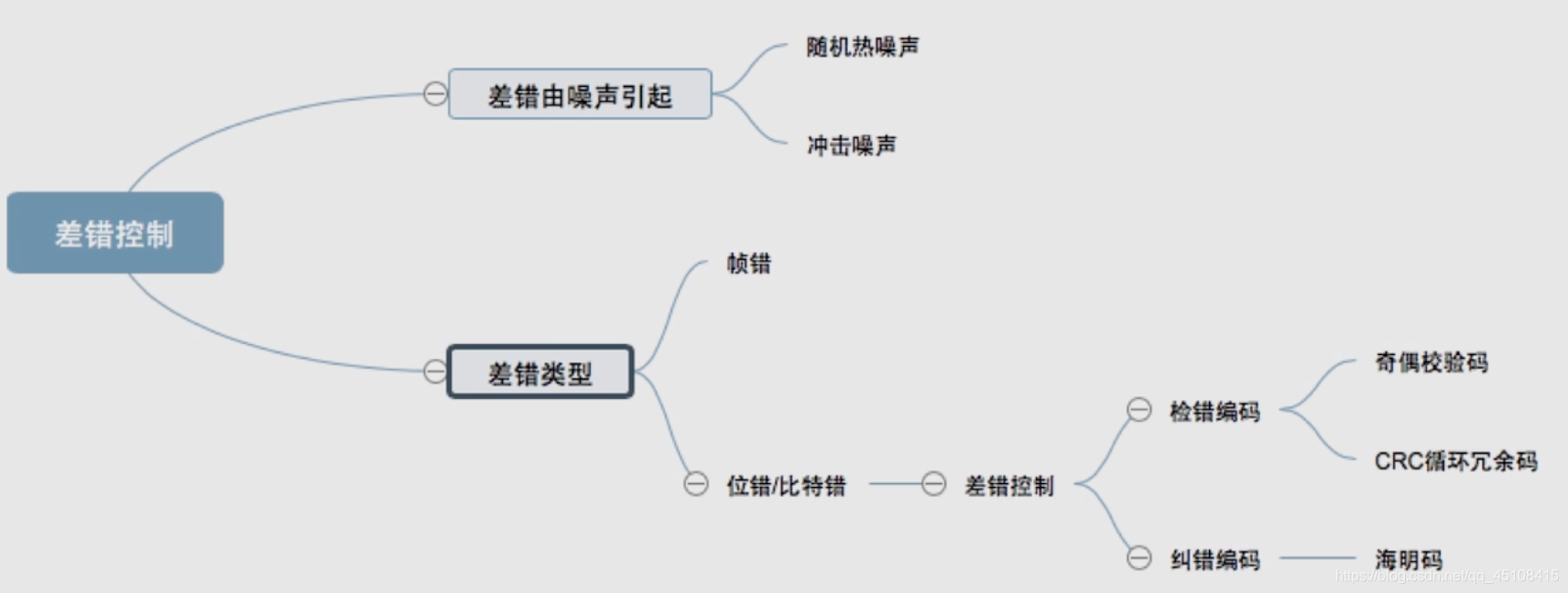
一. 差错控制简介

• 差错是由噪声引起的

• 全局性：固有噪声，随机存在。
  解决方法：提高信噪比来减小干扰

• 局部性：由外界原因导致的冲击噪声，是差错的主要原因
  解决方法：通常是用编码技术

• 差错类型：帧错 & 位错
  1）帧错：三种类型，以传输[1]、[2]、[3]三个帧为例子
  a.丢失：只收到[1] [3]——丢失了[2]
  b.重复：收到了[1] [2] [2] [3]——[2]重复了。
  c.失序：收到[1] [3] [2]——[2]和[3]的顺序错了。

  2）位错：比特位出错，1变成0，或者0变成1。

二.补充知识

• 为什么要进行差错控制：可以节约资源，提升效率。
• 同样是编码，物理层面向单个比特，而数据链路层面向的是一组比特
• 数据链路层都是用冗余编码技术检错

三. 检错编码

开始到本文重点了。
检错编码分为奇偶检验码与CRC循环冗余码。
特点：只能检查出了错，具体错在哪位并不清楚。

（1）奇偶检验码

组成：

由第1位的检验元，与后n-1位的信息元组成。

可以是奇检验码，也可以是偶检验码。区别在于检验码中为’1’的比特的数量是奇数还是偶数。

构造方法：以奇检验码为例。

1）首先计算为’1’的比特的数量。
2）如果1）中结果为偶数，则检验元设为1（让偶变奇），否则检验元设为0（保持偶）

举个例子：

检验码求法：

传输数据1100101有4个’1’，因此我们把检验元设置为1，得到奇检验码为1 1100101。

错误检测方法：

我们可以看到，选项中，ABC的’1’都是偶数个，说明我们传输的奇检测码出错了。而D选项，我们很容易看出传输出了错，但是由于D选项的‘1’也是奇数个，因此这种检验码无法检测出它的错误。

特点

只能检查出奇数个数比特的错误，检错能力为50%。
（这个特点可以自己思考一下，原理挺简单的）

（2）CRC循环冗余检验码

三要素：

• 传输数据
• 生成多项式
• 冗余码/FCS帧检验序列

可参考这个图片的例子理解

考察点：冗余码的计算

1） 加0

根据生成多项式的阶数，给传输数据加0

2）模2除法

用经过1)步骤后的传输数据除以生成多项式，来获得冗余码。
除法过程中用到的不是减法，而是异或。

3）来个例子吧！

图片可能有点乱，见谅= =

检验码获取

在这个例子中，我们就是用到的异或除法来获取冗余码。
由此，我们得到了检验码
数据 + 冗余码：1101 0110 11 1110（粗体为冗余码）

检错部分

左边为具体过程，右边为过程描述。
概括起来就是：接收端对接受到的数据，用同样的除数（本例中为10011）进行同样的异或除法。如果余数为0，说明没错。

3）检错编码后言

总结一下下图，就是：

1. 凡是接收端数据链路层接收的帧均认为无差错（接近1的概率）
2. CRC实现无比特差错传输，但还并不是可靠传输
3. 可靠传输：数据链路层发送端发送什么，接收端就收到什么。
   

三. 纠错编码（海明码）

1）海明码特点

发现双比特错，纠正单比特错

2）工作原理

动一发而牵全身。
也就是一个比特，被多个检验码检验。

3）工作流程

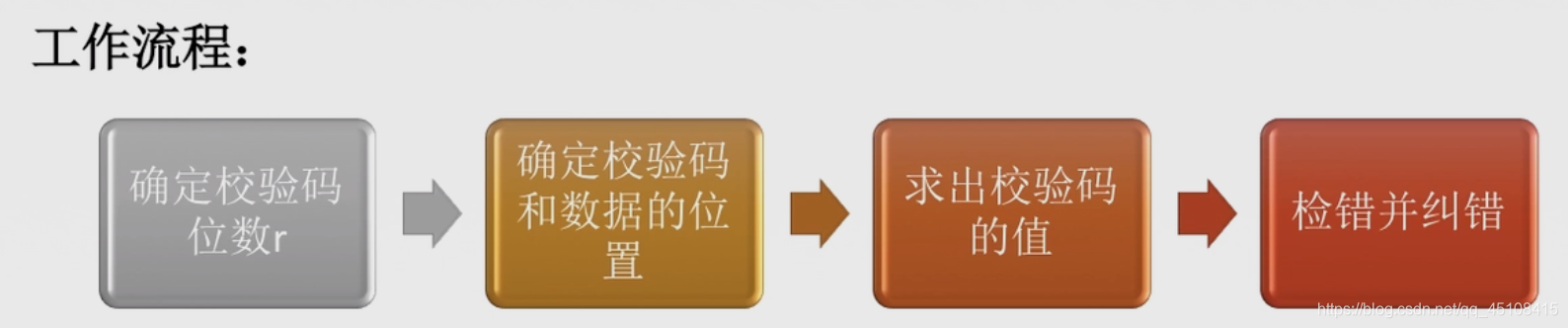
接下来根据顺序来进行工作流程的描述。

I. 确定检验码位数r

依据就是这个海明不等式，图片右边是例子。

II. 确定检验码位置

由I确定检验码有4位，即P1,P2,P3,P4。

检验码放置有一个要求：放置于2的n次方位置
在这里就是1，2，4，8四个下标。

接下来，按顺序把传输数据分别填入剩下的空位。同时把传输数据的实际值也填好。

III. 求出检验码的值

首先我们要知道，每个检验码分别控制哪些数据。
现在更换数据位的进制，换成二进制。

检验码控制数据，是按照其占据数据位的二进制的1的位置来判断的。
如果某个数据占据的数据位，在相同位置也有1，那么这个数据被该检验码控制。
比如此处的P1，占据0001的位置，那么0011、0101、0111、1001都被P1控制，也就是D1、D2、D4、D5被控制。

接下来根据这个性质，就可以求出P1的实际值

检验码和所有控制值的异或，最终结果为0

假设值为X，有 X ⊕ D1 ⊕ D2 ⊕ D4 ⊕ D5 = 0
带入实际值，有 X ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 0 = 0
由此有 X ⊕ 0 = 0，从而得出 X = 0。

以此类推，依次求出P2、P3、P4即可。

由此可知海明码：0010 0111 01

IV. 检错并纠错

此处只需令所有检验码进行和III相同的异或计算即可。

偷懒了，不过ppt写得很清楚，就直接摆上来了。