官方给我们提供了UIExplorer项目，这里边包含React Native的基本所有组件的使用介绍和方法。

运行官方DEMO步骤如下

• 安装react native环境
• React Native项目源码下载
• 下载安装cygwin软件
• 下载安装NDK然后安装以及配置
• 添加Node依赖模块:该命令行需要切到react-native项目中,主要运行如下命令
  cd react-native以及npm install(这里发生错误，是因为npm需要升级的缘故)
• 还需要安装配置python2版本，python3不行
• 开始编译官方实例UIExploerer项目
  打开之前安装的cygwin终端，切换到当前react-native项目中。注意切换路径方法以实际项目路径为准,运行以下命令
  ./gradlew :Examples:UIExplorer:android:app:installDebug
  需要下载很多东西，挺慢的，而且由于网络原因，经常会失败，多试几次才行
• 接下来就是最关键的一步啦~执行如下命令进行打包启动服务.
  ./packager/packager.sh

References

windows版本编译运行react-native官方实例

效果如下

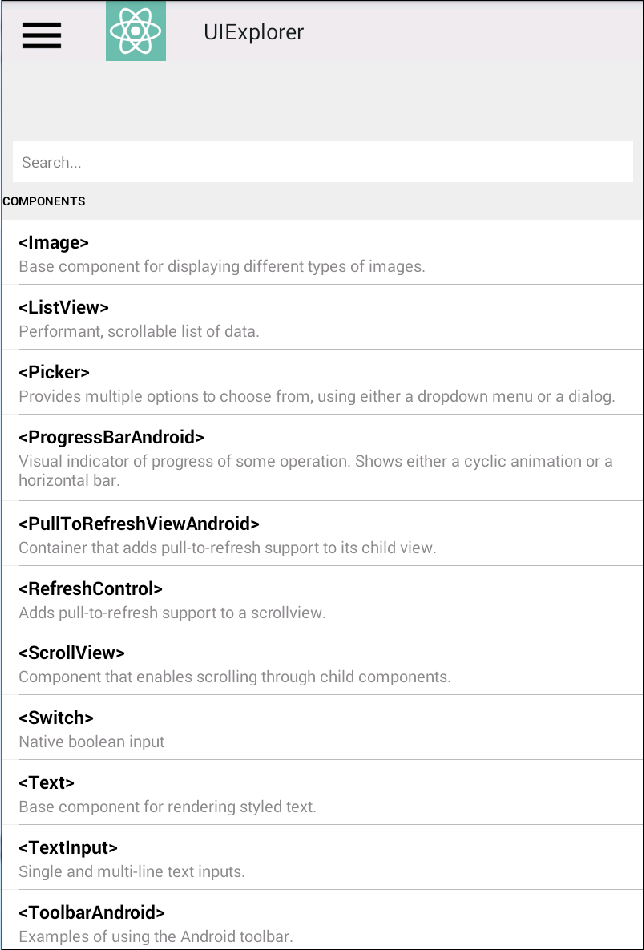
该DEMO包含了react native主要组件与API的实例

COMPONETS

• ActivityIndicatorExample
• SliderExample
• ImageExample
• ListViewExample等

AIPS

• AccessibilityAndroidExample
• AlertExample
• AppStateExample
• BorderExample

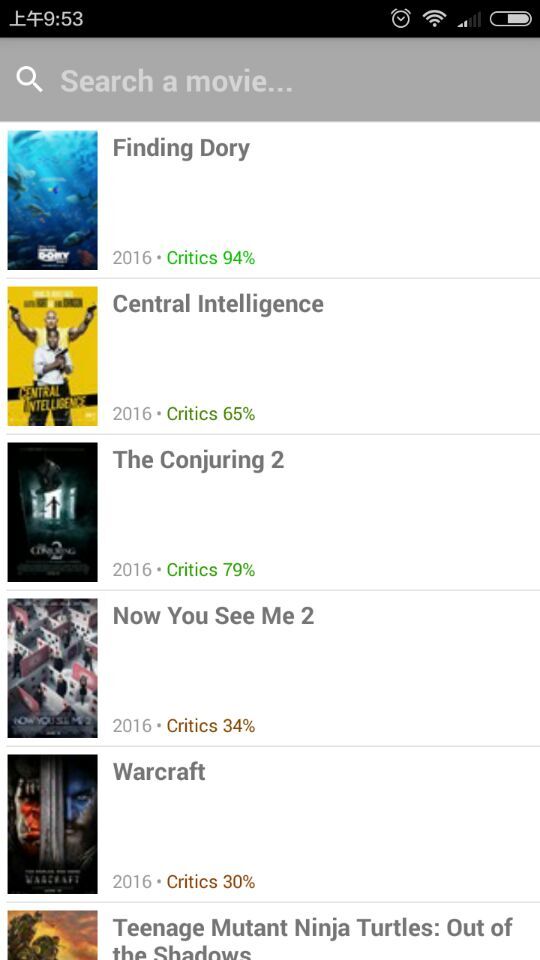
官方Movie实例

The Movies app is a demonstration of basic concepts, such as fetching data, rendering a list of data including images, and navigating between different screens.

Running this app

Before running the app, make sure you ran:

git clone https://github.com/facebook/react-native.git
cd react-native
npm install

Running on Android

You’ll need to have all the prerequisites (SDK, NDK) for Building React Native installed.

Start an Android emulator (Genymotion is recommended).

cd react-native
./gradlew :Examples:Movies:android:app:installDebug
./packager/packager.sh

Note: Building for the first time can take a while.

Open the Movies app in your emulator.

See Running on Device in case you want to use a physical device.

effect