数据结构之DFS与BFS实现

本文主要包括以下内容

  1. 邻接矩阵实现无向图的BFS与DFS
  2. 邻接表实现无向图的BFS与DFS

理论介绍

深度优先搜索介绍

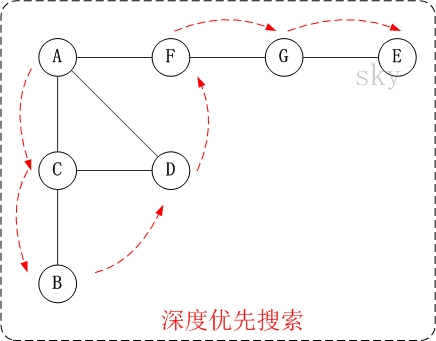
图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。

它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

显然，深度优先搜索是一个递归的过程。

广度优先搜索介绍

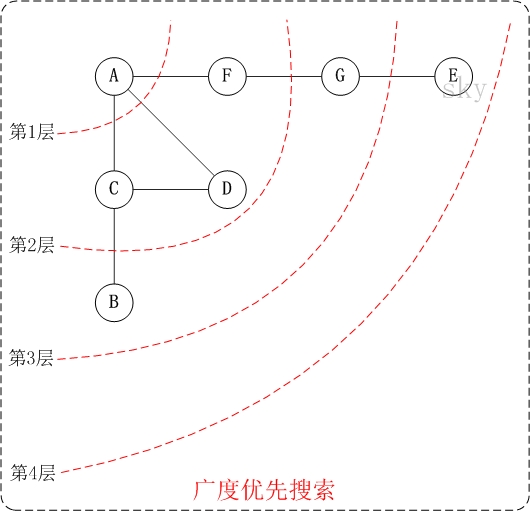
广度优先搜索算法(Breadth First Search)，又称为”宽度优先搜索”或”横向优先搜索”，简称BFS。

它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2…的顶点。

邻接矩阵实现无向图的BFS与DFS

/*** C++: 邻接矩阵表示的"无向图(Matrix Undirected Graph)"** @author skywang* @date 2014/04/19*/#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;#define MAX 100
class MatrixUDG {private:char mVexs[MAX];    // 顶点集合int mVexNum;             // 顶点数int mEdgNum;             // 边数int mMatrix[MAX][MAX];   // 邻接矩阵public:// 创建图(自己输入数据)MatrixUDG();// 创建图(用已提供的矩阵)MatrixUDG(char vexs[], int vlen, char edges[][2], int elen);~MatrixUDG();// 深度优先搜索遍历图void DFS();// 广度优先搜索（类似于树的层次遍历）void BFS();// 打印矩阵队列图void print();private:// 读取一个输入字符char readChar();// 返回ch在mMatrix矩阵中的位置int getPosition(char ch);// 返回顶点v的第一个邻接顶点的索引，失败则返回-1int firstVertex(int v);// 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1int nextVertex(int v, int w);// 深度优先搜索遍历图的递归实现void DFS(int i, int *visited);};/* * 创建图(自己输入数据)*/
MatrixUDG::MatrixUDG()
{char c1, c2;int i, p1, p2;// 输入"顶点数"和"边数"cout << "input vertex number: ";cin >> mVexNum;cout << "input edge number: ";cin >> mEdgNum;if ( mVexNum < 1 || mEdgNum < 1 || (mEdgNum > (mVexNum * (mVexNum-1)))){cout << "input error: invalid parameters!" << endl;return ;}// 初始化"顶点"for (i = 0; i < mVexNum; i++){cout << "vertex(" << i << "): ";mVexs[i] = readChar();}// 初始化"边"for (i = 0; i < mEdgNum; i++){// 读取边的起始顶点和结束顶点cout << "edge(" << i << "): ";c1 = readChar();c2 = readChar();p1 = getPosition(c1);p2 = getPosition(c2);if (p1==-1 || p2==-1){cout << "input error: invalid edge!" << endl;return ;}mMatrix[p1][p2] = 1;mMatrix[p2][p1] = 1;}
}/** 创建图(用已提供的矩阵)** 参数说明：*     vexs  -- 顶点数组*     vlen  -- 顶点数组的长度*     edges -- 边数组*     elen  -- 边数组的长度*/
MatrixUDG::MatrixUDG(char vexs[], int vlen, char edges[][2], int elen)
{int i, p1, p2;// 初始化"顶点数"和"边数"mVexNum = vlen;mEdgNum = elen;// 初始化"顶点"for (i = 0; i < mVexNum; i++)mVexs[i] = vexs[i];// 初始化"边"for (i = 0; i < mEdgNum; i++){// 读取边的起始顶点和结束顶点p1 = getPosition(edges[i][0]);p2 = getPosition(edges[i][1]);mMatrix[p1][p2] = 1;mMatrix[p2][p1] = 1;}
}/* * 析构函数*/
MatrixUDG::~MatrixUDG() 
{
}/** 返回ch在mMatrix矩阵中的位置*/
int MatrixUDG::getPosition(char ch)
{int i;for(i=0; i<mVexNum; i++)if(mVexs[i]==ch)return i;return -1;
}/** 读取一个输入字符*/
char MatrixUDG::readChar()
{char ch;do {cin >> ch;} while(!((ch>='a'&&ch<='z') || (ch>='A'&&ch<='Z')));return ch;
}/** 返回顶点v的第一个邻接顶点的索引，失败则返回-1*/
int MatrixUDG::firstVertex(int v)
{int i;if (v<0 || v>(mVexNum-1))return -1;for (i = 0; i < mVexNum; i++)if (mMatrix[v][i] == 1)return i;return -1;
}/** 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1*/
int MatrixUDG::nextVertex(int v, int w)
{int i;if (v<0 || v>(mVexNum-1) || w<0 || w>(mVexNum-1))return -1;for (i = w + 1; i < mVexNum; i++)if (mMatrix[v][i] == 1)return i;return -1;
}/** 深度优先搜索遍历图的递归实现*/
void MatrixUDG::DFS(int i, int *visited)
{int w;visited[i] = 1;cout << mVexs[i] << " ";// 遍历该顶点的所有邻接顶点。若是没有访问过，那么继续往下走for (w = firstVertex(i); w >= 0; w = nextVertex(i, w)){if (!visited[w])DFS(w, visited);}}/** 深度优先搜索遍历图*/
void MatrixUDG::DFS()
{int i;int visited[MAX];       // 顶点访问标记// 初始化所有顶点都没有被访问for (i = 0; i < mVexNum; i++)visited[i] = 0;cout << "DFS: ";for (i = 0; i < mVexNum; i++){//printf("\n== LOOP(%d)\n", i);if (!visited[i])DFS(i, visited);}cout << endl;
}/** 广度优先搜索（类似于树的层次遍历）*/
void MatrixUDG::BFS()
{int head = 0;int rear = 0;int queue[MAX];     // 辅组队列int visited[MAX];   // 顶点访问标记int i, j, k;for (i = 0; i < mVexNum; i++)visited[i] = 0;cout << "BFS: ";for (i = 0; i < mVexNum; i++){if (!visited[i]){visited[i] = 1;cout << mVexs[i] << " ";queue[rear++] = i;  // 入队列}while (head != rear) {j = queue[head++];  // 出队列for (k = firstVertex(j); k >= 0; k = nextVertex(j, k)) //k是为访问的邻接顶点{if (!visited[k]){visited[k] = 1;cout << mVexs[k] << " ";queue[rear++] = k;}}}}cout << endl;
}/** 打印矩阵队列图*/
void MatrixUDG::print()
{int i,j;cout << "Martix Graph:" << endl;for (i = 0; i < mVexNum; i++){for (j = 0; j < mVexNum; j++)cout << mMatrix[i][j] << " ";cout << endl;}
}int main()
{char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};char edges[][2] = {{'A', 'C'}, {'A', 'D'}, {'A', 'F'}, {'B', 'C'}, {'C', 'D'}, {'E', 'G'}, {'F', 'G'}};int vlen = sizeof(vexs)/sizeof(vexs[0]);int elen = sizeof(edges)/sizeof(edges[0]);MatrixUDG* pG;// 自定义"图"(输入矩阵队列)//pG = new MatrixUDG();// 采用已有的"图"pG = new MatrixUDG(vexs, vlen, edges, elen);pG->print();   // 打印图pG->DFS();     // 深度优先遍历pG->BFS();     // 广度优先遍历return 0;
}

邻接表实现无向图的BFS与DFS

/*** C++: 邻接表表示的"无向图(List Undirected Graph)"** @author skywang* @date 2014/04/19*/#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;#define MAX 100
// 邻接表
class ListUDG
{private: // 内部类// 邻接表中表对应的链表的顶点class ENode{public:int ivex;           // 该边所指向的顶点的位置ENode *nextEdge;    // 指向下一条弧的指针};// 邻接表中表的顶点class VNode{public:char data;          // 顶点信息ENode *firstEdge;   // 指向第一条依附该顶点的弧};private: // 私有成员int mVexNum;             // 图的顶点的数目int mEdgNum;             // 图的边的数目VNode mVexs[MAX];public:// 创建邻接表对应的图(自己输入)ListUDG();// 创建邻接表对应的图(用已提供的数据)ListUDG(char vexs[], int vlen, char edges[][2], int elen);~ListUDG();// 深度优先搜索遍历图void DFS();// 广度优先搜索（类似于树的层次遍历）void BFS();// 打印邻接表图void print();private:// 读取一个输入字符char readChar();// 返回ch的位置int getPosition(char ch);// 深度优先搜索遍历图的递归实现void DFS(int i, int *visited);// 将node节点链接到list的最后void linkLast(ENode *list, ENode *node);
};/** 创建邻接表对应的图(自己输入)*/
ListUDG::ListUDG()
{char c1, c2;int v, e;int i, p1, p2;ENode *node1, *node2;// 输入"顶点数"和"边数"cout << "input vertex number: ";cin >> mVexNum;cout << "input edge number: ";cin >> mEdgNum;if ( mVexNum < 1 || mEdgNum < 1 || (mEdgNum > (mVexNum * (mVexNum-1)))){cout << "input error: invalid parameters!" << endl;return ;}// 初始化"邻接表"的顶点for(i=0; i<mVexNum; i++){cout << "vertex(" << i << "): ";mVexs[i].data = readChar();mVexs[i].firstEdge = NULL;}// 初始化"邻接表"的边for(i=0; i<mEdgNum; i++){// 读取边的起始顶点和结束顶点cout << "edge(" << i << "): ";c1 = readChar();c2 = readChar();p1 = getPosition(c1);p2 = getPosition(c2);// 初始化node1node1 = new ENode();node1->ivex = p2;// 将node1链接到"p1所在链表的末尾"if(mVexs[p1].firstEdge == NULL)mVexs[p1].firstEdge = node1;elselinkLast(mVexs[p1].firstEdge, node1);// 初始化node2node2 = new ENode();node2->ivex = p1;// 将node2链接到"p2所在链表的末尾"if(mVexs[p2].firstEdge == NULL)mVexs[p2].firstEdge = node2;elselinkLast(mVexs[p2].firstEdge, node2);}
}/** 创建邻接表对应的图(用已提供的数据)*/
ListUDG::ListUDG(char vexs[], int vlen, char edges[][2], int elen)
{char c1, c2;int i, p1, p2;ENode *node1, *node2;// 初始化"顶点数"和"边数"mVexNum = vlen;mEdgNum = elen;// 初始化"邻接表"的顶点for(i=0; i<mVexNum; i++){mVexs[i].data = vexs[i];mVexs[i].firstEdge = NULL;}// 初始化"邻接表"的边for(i=0; i<mEdgNum; i++){// 读取边的起始顶点和结束顶点c1 = edges[i][0];c2 = edges[i][1];p1 = getPosition(c1);p2 = getPosition(c2);// 初始化node1node1 = new ENode();node1->ivex = p2;// 将node1链接到"p1所在链表的末尾"if(mVexs[p1].firstEdge == NULL)mVexs[p1].firstEdge = node1;elselinkLast(mVexs[p1].firstEdge, node1);// 初始化node2node2 = new ENode();node2->ivex = p1;// 将node2链接到"p2所在链表的末尾"if(mVexs[p2].firstEdge == NULL)mVexs[p2].firstEdge = node2;elselinkLast(mVexs[p2].firstEdge, node2);}
}/* * 析构函数*/
ListUDG::~ListUDG() 
{
}/** 将node节点链接到list的最后*/
void ListUDG::linkLast(ENode *list, ENode *node)
{ENode *p = list;while(p->nextEdge)p = p->nextEdge;p->nextEdge = node;
}/** 返回ch的位置*/
int ListUDG::getPosition(char ch)
{int i;for(i=0; i<mVexNum; i++)if(mVexs[i].data==ch)return i;return -1;
}/** 读取一个输入字符*/
char ListUDG::readChar()
{char ch;do {cin >> ch;} while(!((ch>='a'&&ch<='z') || (ch>='A'&&ch<='Z')));return ch;
}/** 深度优先搜索遍历图的递归实现*/
void ListUDG::DFS(int i, int *visited)
{ENode *node;visited[i] = 1;cout << mVexs[i].data << " ";node = mVexs[i].firstEdge;while (node != NULL){if (!visited[node->ivex])DFS(node->ivex, visited);node = node->nextEdge;}
}/** 深度优先搜索遍历图*/
void ListUDG::DFS()
{int i;int visited[MAX];       // 顶点访问标记// 初始化所有顶点都没有被访问for (i = 0; i < mVexNum; i++)visited[i] = 0;cout << "DFS: ";for (i = 0; i < mVexNum; i++){if (!visited[i])DFS(i, visited);}cout << endl;
}/** 广度优先搜索（类似于树的层次遍历）*/
void ListUDG::BFS()
{int head = 0;int rear = 0;int queue[MAX];     // 辅组队列int visited[MAX];   // 顶点访问标记int i, j, k;ENode *node;for (i = 0; i < mVexNum; i++)visited[i] = 0;cout << "BFS: ";for (i = 0; i < mVexNum; i++){if (!visited[i]){visited[i] = 1;cout << mVexs[i].data << " ";queue[rear++] = i;  // 入队列}while (head != rear) {j = queue[head++];  // 出队列node = mVexs[j].firstEdge;while (node != NULL){k = node->ivex;if (!visited[k]){visited[k] = 1;cout << mVexs[k].data << " ";queue[rear++] = k;}node = node->nextEdge;}}}cout << endl;
}/** 打印邻接表图*/
void ListUDG::print()
{int i,j;ENode *node;cout << "List Graph:" << endl;for (i = 0; i < mVexNum; i++){cout << i << "(" << mVexs[i].data << "): ";node = mVexs[i].firstEdge;while (node != NULL){cout << node->ivex << "(" << mVexs[node->ivex].data << ") ";node = node->nextEdge;}cout << endl;}
}int main()
{char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};char edges[][2] = {{'A', 'C'}, {'A', 'D'}, {'A', 'F'}, {'B', 'C'}, {'C', 'D'}, {'E', 'G'}, {'F', 'G'}};int vlen = sizeof(vexs)/sizeof(vexs[0]);int elen = sizeof(edges)/sizeof(edges[0]);ListUDG* pG;// 自定义"图"(输入矩阵队列)//pG = new ListUDG();// 采用已有的"图"pG = new ListUDG(vexs, vlen, edges, elen);pG->print();   // 打印图pG->DFS();     // 深度优先遍历pG->BFS();     // 广度优先遍历return 0;
}

References

图的遍历之 深度优先搜索和广度优先搜索 - 如果天空不死 - 博客园

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/493978.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

一图分析华为最新AI生态与未来趋势

一图分析华为最新AI生态与未来趋势

华为全联接大会2018年10月10日在上海召开&#xff0c;作为面向ICT产业的年度大会&#xff0c;华为公布了重要AI战略&#xff0c;将华为AI发展战略概括为以下五大方向&#xff1a;强力投资基础研究、打造全栈解决方案、投资开放生态和人才培养、解决方案增强以及内部效率提升。华…
阅读更多...
在读博士的第八年，她破解了量子计算领域最基本的问题之一

在读博士的第八年，她破解了量子计算领域最基本的问题之一

来源&#xff1a;原理Urmila Mahadev&#xff08;厄米拉马哈德夫&#xff09;花了八年时间在研究生院解决了量子计算领域最基本的问题之一&#xff1a;怎么知道量子计算机是否做了量子计算呢&#xff1f;2017年春天&#xff0c;Urmila Mahadev发现自己处于大多数研究生都会认为…
阅读更多...
React Native实例之房产搜索APP

React Native实例之房产搜索APP

React Native 开发越来越火了&#xff0c;web app也是未来的潮流, 现在react native已经可以完成一些最基本的功能. 通过开发一些简单的应用, 可以更加熟练的掌握 RN 的知识. 在学习的过程&#xff0c;发现了一个房产搜索APP的实例&#xff0c;但只有ios版本&#xff0c; 本文…
阅读更多...
“间谍芯片”疑云：谁在撒谎？警示何在？

“间谍芯片”疑云：谁在撒谎？警示何在？

芯片级安全没有终点来演&#xff1a;科学网摘要&#xff1a;10月5日起&#xff0c;一则“苹果、亚马逊被卷入&#xff0c;中国黑客利用微芯片入侵美国”的消息不胫而走&#xff0c;消息所波及的中美科技企业的股价应声下跌。10月5日起&#xff0c;一则“苹果、亚马逊被卷入&…
阅读更多...
Extjs4前端开发代码规范参考

Extjs4前端开发代码规范参考

准则&#xff1a; 一致性&#xff0c; 隔离与统一管理&#xff0c; 螺旋式重构改进&#xff0c; 消除重复&#xff0c; 借鉴现有方案 1. 保证系统实现的一致性&#xff0c;寻求一致性方案&#xff0c; 相同或相似功能尽量用统一模式处理&#xff1b; 2. 尽可能使用隔离技…
阅读更多...
数据结构之最小生成树

数据结构之最小生成树

prime算法 普里姆(Prim)算法&#xff0c;是用来求加权连通图的最小生成树的算法。 基本思想 对于图G而言&#xff0c;V是所有顶点的集合&#xff1b;现在&#xff0c;设置两个新的集合U和T&#xff0c;其中U用于存放G的最小生成树中的顶点&#xff0c;T存放G的最小生成树中…
阅读更多...
打造无所不及的智能：徐直军发布华为AI战略及全栈全场景方案

打造无所不及的智能：徐直军发布华为AI战略及全栈全场景方案

来源&#xff1a;C114通信网摘要&#xff1a;选择正确的问题比寻找新奇的方案更重要。“这是一个伟大的时代&#xff0c;华为立志为推动人类进步和世界繁荣做出贡献。2017年底&#xff0c;我们提出了新的愿景和使命&#xff0c;‘把数字世界带入每个人、每个家庭、每个组织&…
阅读更多...
同步博客到CSDN

同步博客到CSDN

经过一些朋友的多次邀请&#xff0c;现同步博客到CSDN&#xff0c;地址:http://blog.csdn.net/knightswarrior。 转载于:https://www.cnblogs.com/KnightsWarrior/p/BackupToCSDN.html
阅读更多...
四超多强 一文看懂中国CV独角兽格局

四超多强 一文看懂中国CV独角兽格局

来源&#xff1a;网易智能通过短短两三年的攻城略地&#xff0c;中国CV&#xff08;Computer Vision&#xff0c;计算机视觉&#xff09;行业形成“四超多强”的格局。商汤、云从、依图、旷视还被称为“四小龙”&#xff0c;他们之间的故事由来已久&#xff0c;谈及最多的当属他…
阅读更多...
http://www.shengshiyouxi.com

http://www.shengshiyouxi.com

android从Linux系统启动有4个步骤&#xff1b; (1) init进程启动 (2) Native服务启动 (3) System Server&#xff0c;Android服务启动 (4) Home启动 总体启动框架图如&#xff1a; 第一步&#xff1a;initial进程(system\core\init) init进程&…
阅读更多...
清华 Aminer 发布最新2018人脸识别研究报告

清华 Aminer 发布最新2018人脸识别研究报告

来源&#xff1a;专知AMiner平台由清华大学计算机系研发&#xff0c;拥有我国完全自主知识产权。平台包含了超过2.3亿学术论文/专利和1.36亿学者的科技图谱&#xff0c;提供学者评价、专家发现、智能指派、学术地图等科技情报专业化服务。 今日&#xff0c;该平台发布最新的201…
阅读更多...
敏捷实践：比每日会议更疯狂的半日会议！

敏捷实践：比每日会议更疯狂的半日会议！

由“每周例会”说起 每天项目例会的话&#xff0c;频率太高了&#xff0c;可能会浪费时间&#xff0c;如果每月一次&#xff0c;似乎时间太长了&#xff0c;于是我们往往会“每周例会”。 有一次我参加了某项目的每周例会&#xff0c;开会的时间是周五&#xff0c;会上其中一位…
阅读更多...
智能生产的现状与未来！

智能生产的现状与未来！

来源&#xff1a;数字化企业北京机械工业自动化研究所首席专家蒋明炜先生是我国最早投身企业管理及其信息化事业的专家之一&#xff0c;积累了宝贵的理论实践经验&#xff0c;在国家提出《中国制造2025》之后&#xff0c;蒋明炜先生作为该领域资深专家&#xff0c;先后组织领导…
阅读更多...
82岁的北大教授证明了黎曼猜想？

82岁的北大教授证明了黎曼猜想？

来源&#xff1a;AI科技大本营最近&#xff0c;黎曼猜想有点热。上个月&#xff0c;89 岁的菲尔兹奖与阿贝尔奖双料得主、英国皇家学会院士迈克尔阿蒂亚爵士&#xff08;Michael Atiyah&#xff09;刚刚宣布自己证明了黎曼猜想。近日&#xff0c;82 岁的北大教授&#xff08;已…
阅读更多...
Atlas机器人再秀逆天操作！波士顿动力科研or商业化，将何去何从？

Atlas机器人再秀逆天操作！波士顿动力科研or商业化，将何去何从？

来源&#xff1a;物联网智库在众多机器人相关的技术公司里&#xff0c;波士顿动力的核心特点在于&#xff0c;他们始终将「仿生」看作机器人设计的最高宗旨。其创始人Raibert 也称自己的目的是建造一种能和动物以及人一模一样的&#xff0c;完成一切事情的机器人。这既是波士顿…
阅读更多...
OpenGL6-纹理动画

OpenGL6-纹理动画

代码下载 #include "CELLWinApp.hpp"#include <gl/GLU.h>#include <assert.h>#include <math.h>#pragma comment(lib,"opengl32.lib")#pragma comment(lib,"glu32.lib")#pragma comment(lib,"winmm.lib") /*** 这个…
阅读更多...
《科学美国人》：美国应保持太空、网络、生物领域的科技优势

《科学美国人》：美国应保持太空、网络、生物领域的科技优势

来源&#xff1a;美国《科学美国人》转自&#xff1a;国防科技要闻&#xff08;ID&#xff1a;CDSTIC&#xff09;作者&#xff1a;军事科学院军事科学信息研究中心 吴海近日&#xff0c;美国《科学美国人》杂志发表《我们准备好迎接未来战争了吗&#xff1f;》一文&#xff…
阅读更多...
微信开发入门

微信开发入门

微信开发需要搭建PHP环境 参考链接&#xff1a;Apache2.2与php5.3.5如何整合&#xff1f;如何能够被使用_百度经验 搭建的过程出现了很多坑&#xff0c;只能小心&#xff0c;重复搭建了&#xff0c;错误原因可能是VC9或VC11环境没有配置的原因&#xff0c;多试试才行。 然后…
阅读更多...
实现计算机界“大满贯”，芮勇博士再获技术成就大奖

实现计算机界“大满贯”，芮勇博士再获技术成就大奖

来源&#xff1a;联想研究院近日&#xff0c;国际计算机协会&#xff08;ACM&#xff09;多媒体专委会&#xff08;Special Interest Group on Multimedia&#xff0c;简称SIGMM&#xff09;2018技术成就奖揭晓了。在全球众多的候选人当中&#xff0c;该奖最终花落联想集团首席…
阅读更多...
机器人流程自动化崛起，中国是否准备好迎接智能自动化时代？

机器人流程自动化崛起，中国是否准备好迎接智能自动化时代？

来源&#xff1a;亿欧智库摘要&#xff1a;机器人流程自动化&#xff08;Robotic Process Automation, RPA&#xff09;正迅速成为企业改善服务、提高效率和降低成本的关键工具。对此&#xff0c;PWC针对国内RPA市场展开了调查&#xff0c;预计未来45%的工作活动可以实现自动化…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023