在本章节中,将介绍几种常用的图像变换的方法,即利用数学公式将图像变换成另一种具有特定物理意义的图像,通过新的图像,我们可以观察出原图像的某些特性,且可以对原图像进行滤波、压缩等图像处理的操作,包括傅里叶变换、沃尔什变换等。
一、图像傅里叶变换基本原理与实现
傅里叶变换,是将时域信号转换为频域信号的变换方法,将时域信号分解为频率不同的正弦波信号的方法,也就是说,任何一个信号都是若干个正弦信号所叠加。通过傅里叶变换,我们就可以得到信号的频率特性,是高频成分多一点,还是低频成分多一点,每个成分的幅值和相位是多少(频谱图和相位图)。
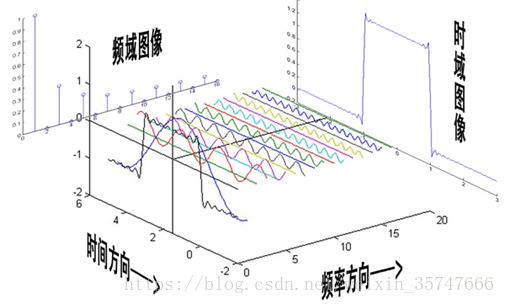
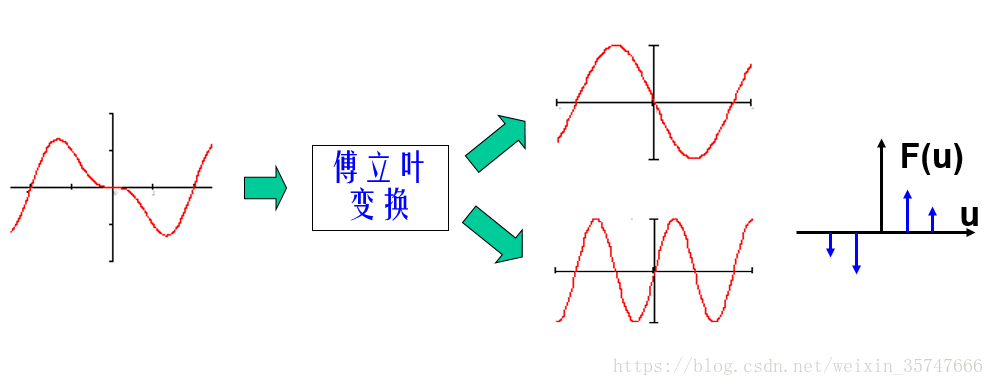
图像是离散的二维信号,可以通过二维傅里叶变换实现到频域的转换,转换前的图像矩阵是由实数组成的,转换后的频域矩阵是复数阵,变换公式如下所示,x,yx,yx,y是图像阵的坐标,u,vu,vu,v是频域阵的坐标,两者没有一一对应的关系,频域阵中每一个点都是对图像阵中每一个像素点进行了运算的。
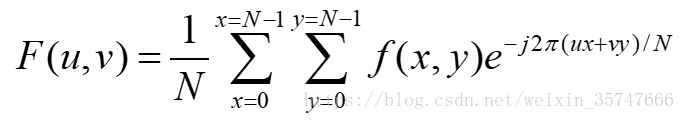
我们关注的是通过傅里叶变换获得图像的频谱图与相位图,计算方法如下,
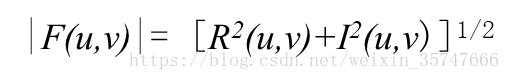
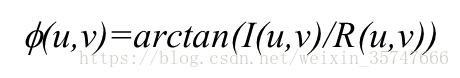
接下来我们用python代码来实现傅里叶变换,得到图像的频谱图与相位图,实验图像是Lena。
计算频谱图的代码如下,
import cv2
import numpy as np
import matplotlib.pyplot as plt
import pylab
img = cv2.imread('Lena.jpg',0)
f = np.fft.fft2(img) #傅里叶变换
fshift = np.fft.fftshift(f) #将零频点移到图像中央
s1 = np.log(np.abs(f)) #先进行绝对值运算,然后取对数,限制数值范围
s2= np.log(np.abs(fshift))
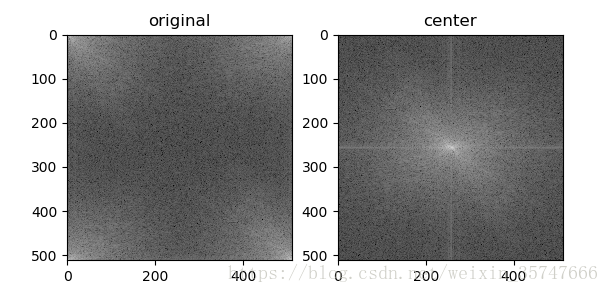
plt.subplot(121),plt.imshow(s1,'gray'),plt.title('original')
plt.subplot(122),plt.imshow(s2,'gray'),plt.title('center')
pylab.show()
得到结果,第一幅图是原始傅里叶变换的结果,我们可以这样理解这幅图片,中心是高频部分,四周是低频部分,横轴是原图片横向方向的傅里叶频谱,纵向是原图片纵向方向的傅里叶频谱,为是频谱具有一致性与可观性,我们将零频点,也就是四个角上的点,移到频谱图的中心得到第二幅图,得到的频谱图中心是低频部分,四周是高频部分。图中高亮的点代表成分多的某一频率,灰暗的点代表成分少的某一频率。如果一幅图片高频部分多是高亮,代表图像尖锐,变化剧烈,边界分明且两边像素差距极大;反之,图片低频部分高亮,高频部分灰暗,代表图片平缓、柔和。
观察实验图像的频谱结果,中心点高亮,低频部分占据成分大,图片总体表现的平缓。
接下来我们来实现相位的部分,实现代码如下,
import cv2
import numpy as np
import matplotlib.pyplot as plt
import pylab
img = cv2.imread('Lena.jpg',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
xw = np.angle(f); #np.angle()函数求相位,arctan(虚部/实部)
xw_shift =np.angle(fshift)
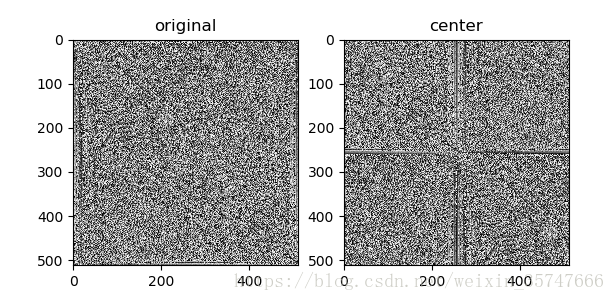
plt.subplot(121),plt.imshow(xw,'gray'),plt.title('original')
plt.subplot(122),plt.imshow(xw_shift,'gray'),plt.title('center')
pylab.show()
得到结果,图中的点代表频谱图中对应频率的相位值。
二、图像傅里叶变换的应用
1、傅里叶变换在图像滤波中的应用
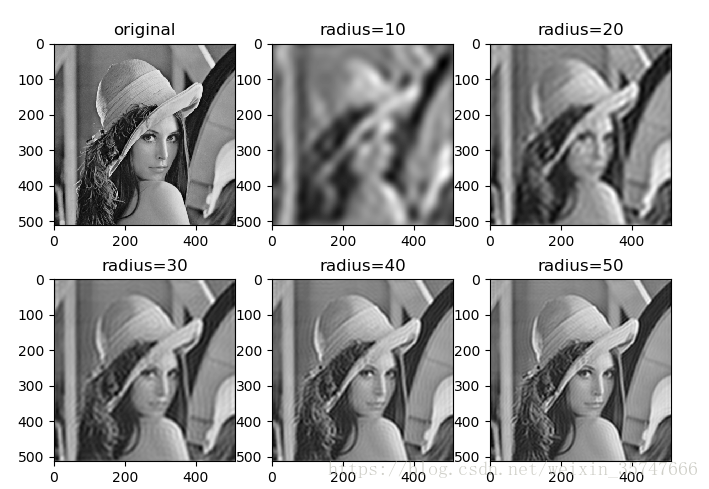
经过傅里叶变换后的图像中间部分为低频部分,越靠外频率越高,因此,我们可以选择所需要的高频或是低频进行滤波。高频反映图像中的细节,低频反映图像中的整体概貌。
低通滤波代码如下,
import cv2
import numpy as np
import matplotlib.pyplot as plt
import pylabdef LPF(img,radius = 50): #定义低通滤波函数,radius:低通半径,半径越小,低通效果越明显,图片越模糊rows,cols = img.shapemrows = int(rows/2)mcols = int(cols/2)mask = np.zeros((rows,cols),np.uint8) #创建掩码mask[mrows-radius:mrows+radius,mcols-radius:mcols+radius] = 1return mask def main():img = cv2.imread('Lena.jpg',0)f = np.fft.fft2(img)fshift = np.fft.fftshift(f) fshift = fshift*LPF(img) #低通滤波,即与掩码相乘,过滤掉频率高的部分#逆变换f_ishift = np.fft.ifftshift(fshift)img_back = np.fft.ifft2(f_ishift)img_back = np.abs(img_back)plt.imshow(img_back,'gray'),plt.title('radius=50')pylab.show()if __name__=="__main__":main()
结果如下,
高通滤波代码如下,
import cv2
import numpy as np
import matplotlib.pyplot as plt
import pylabdef HPF(img,radius= 50): #高通滤波函数,radius:高通半径,半径越大,高通效果越明显,图片越尖锐rows,cols = img.shapemrows = int(rows/2)mcols = int(cols/2)mask = np.zeros((rows,cols),np.uint8) #创建掩码mask[:,:] = 1mask[mrows-radius:mrows+radius,mcols-radius:mcols+radius] = 0return mask def main():img = cv2.imread('Lena.jpg',0)f = np.fft.fft2(img)fshift = np.fft.fftshift(f) fshift = fshift*HPF(img,1) #高通滤波,即与掩码相乘,过滤掉频率高的部分#逆变换f_ishift = np.fft.ifftshift(fshift) img_back = np.fft.ifft2(f_ishift)img_back = np.abs(img_back)plt.imshow(img_back,'gray'),plt.title('radius=50')pylab.show()if __name__=="__main__":main()
结果如下,
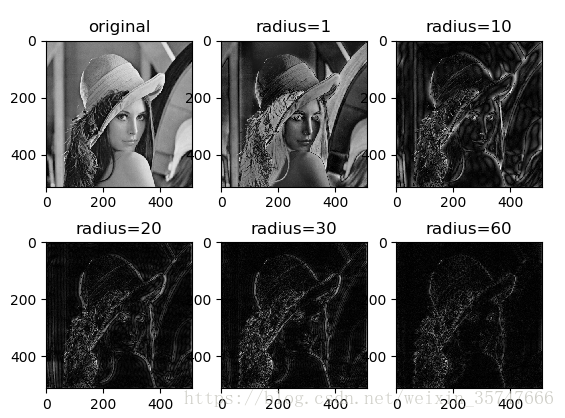
对比结果可以发现,低通滤波让图片变得更加模糊,过滤掉了图片中边缘的、尖锐的部分;高通滤波让图片变得更加尖锐,过滤掉了图片中平缓的部分,留下边缘的、尖锐的部分。
2、傅里叶变换在图像压缩中的应用
原理很简单,将高频系数设置为0,压缩效果如下,


未完待续




图像增强1)
图像增强2)



图像增强3)










